矛盾之谜：频谱效率与功率效率

假设AWGN信道带宽为W，噪声功率谱密度为n₀。若现在想以比特率R（单位：bit/s）来无误传输，那每比特平均至少需要多少功率呢？记每比特需要功率为E_b。首先，信号花费的总功率为E_bR，AWGN噪声总功率为n₀W，根据香农容量公式可知，此时能无误传输的最高比特率为

显然，必须有R≤C，则

令r=R/W为频谱效率，即单位带宽内的比特速率，由上式继续可得

其推导中用到

从而可知，当r→0时，即频谱效率很低时，上面式（11-31）中展开带r的项都趋近于0，有

也就是说，当维持在一个频谱效率很低的区域里传输时，若每比特平均功率E_b达到一个常数n₀×ln2，理论上就可以无误传输了。在这个频谱效率很低的区域内，比特率R增减时（增减后保证频谱效率还是不超出该区域），信号总功率RE_b=R×n₀×ln2也只需要相应比例地线性增减即可无误传输。反过来看，要想增大比特率R，可以保持W不变，增加功率就好，并且效果也还不错（线性增长）。但是请考虑，在这个低频谱效率区域内，增大带宽能有什么用？没有用！因为在低频谱效率区域内，每个比特能无误传输需要的功率和带宽无关，就是常数n₀ln2。所以，如果此时信号功率只有P，那么最多就只能支持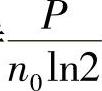比特的无误传输，哪怕信号带宽增加到无穷大。这个结论我们在11.4.1节其实已经看到了，即当带宽趋于无穷大时，容量趋于1.44P/n₀。可以看到，在低频谱效率区域，能无误传输的比特率不取决于带宽，而是取决于信号功率，即受限于能提供的信号功率，所以低频谱效率区域也被称为功率受限区域。(www.xing528.com)

当频谱效率较高时，比如r>1，上面式（11-31）中展开带r的项，随着r增长，增长都超快（级数增长）。r增长，即R增长，且此时E_b也超快增长，需要的总功率E_bR也就需要超快增长才能保证以比特率R无误传输；R要想增长一点，要以信号功率E_bR增长很多为代价。可以看到，对于已经在高谱效率区域运行时，想通过信号功率来换取比特率的进一步增长太吃亏了，怎么办呢？那别让它在高频谱效率区域内运行，从而降低频谱效率。有一个办法就是增加带宽。只要频谱效率降一点，每比特无误传输需要的平均功率就（指数）下降，对于给定量的信号功率来说，就可以支持更高比特率的无误传输。换句话说，当在高频谱效率区域时，有多少信号功率都白搭，关键看有多少带宽，即受限于带宽，因此高谱效率区域也被称为带宽受限区域。

总之，当谱效率r维持较小时，提高一点功率，理论上能无误传输的比特率R可以同比例线性提高；当谱效率r维持较高时，提高很多功率，才能换来R提高一点。

三言两语

这里就有个矛盾，若想功率有效利用，就得维持低谱效率；若想维持高谱效率，就得牺牲功率有效利用率。这个矛盾可以由如下的思想解决：如果有机会在占用带宽不变的情况下，能构造出多个平行信道，每个信道带宽一样，然后把总功率分配到多个平行信道上，这样使得每个信道维持在低谱效率，但功率能得到有效利用，最后多个平行信道加起来的谱效率还是挺高的。多天线技术MIMO空分复用的一部分效果就是利用该思想，以后我们再具体分析讨论。