带宽与功率的平衡效应

记信号与噪声功率比SNR=P/σ²。为了达到相同信道容量，信噪比SNR和带宽W可以互换（注意暂时没说信号功率和带宽可以互换），即降低SNR但增加带宽W或反之。注意在AWGN下，香农容量公式可以写成

其中，n₀为白噪声功率谱密度，是人为不可控的，它是多少就是多少，我们拿它毫无办法。我们能改变的只有系统带宽W和信号功率P。另一方面，我们注意到，随着W增大，即使信号功率P保持不变，信噪比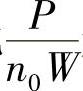天然就在降低，即信噪比SNR和带宽W很自然地就在“互换”。注意，我们想要的其实是带宽W和信号功率P之间的互换，即达到相同信道容量，如果增加带宽W，最好能减少（节省）信号功率P或反之。若达到相同信道容量，带宽W增加了，而信号功率P却不能降低，那为何要增加带宽？也就是说，在增加带宽时，即使信噪比天然已经在降低了，我们还可以进一步降低信号功率P来进一步降低信噪比。

进一步应该有下面的关系成立，这个“互换”才有意义：

而事实上，这个关系成立吗？答案是肯定的。进一步地，可以得出以下两个结论：(www.xing528.com)

1）当SNR趋于无穷大时，带宽W可以保持不变，比如只增加发射功率P，从而信道容量趋于无穷大。

2）当W趋于无穷大时，即使信号功率P保持不变，信道容量却趋于某有限常数。原因是前面已经说过的，带宽变化时，即使信号功率P保持不变，SNR不可能保持不变，因为一般噪声的功率谱是分布在无穷大带宽上的。那么，当带宽W趋于无穷大时，噪声功率也趋于无穷大，从而SNR趋于无穷小，所以信道容量不会趋于无穷大。具体地，假设噪声是白噪声，功率谱密度为n₀，则

上面的极限推导用到等价无穷小量关系