增添色彩，别让白噪声烦扰

前面讲了加性高斯白噪声和一般白噪声的信道容量，现在我们丰富一下，引入一些色彩，即讨论噪声功率谱非常数的一般加性噪声信道的信道容量。

对于一定带宽的有色噪声，虽然整个带宽上功率谱不是常数，但可以把噪声分解成若干窄带的噪声，每个窄带噪声的功率谱近似平坦为常数，这样我们可以把这些窄带噪声分别独立地按AWGN处理，从而可以应用AWGN的结果。

假设带宽仍然为W，噪声功率谱为P_N（f），信号功率谱为P_x（f），则对窄带宽ω<f<ω+△ω上应用香农公式得，该窄带上信道容量为

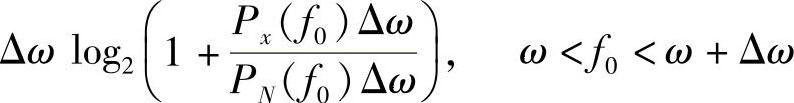
对所有窄带求和，取极限得总容量为

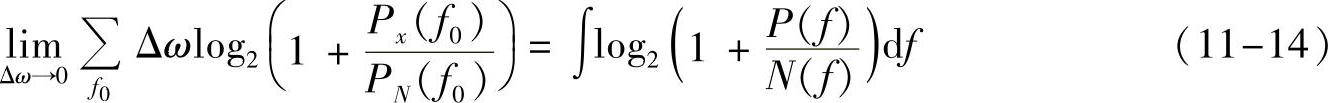
注意，这里各个窄带需要分别独立编码，使各自分别达到信道容量，最后和容量才能达到最大。

现在假设信号总功率一定，即

∫P_x（f）df=P怎样的P_x（f），或者说怎样在整个频带上分配功率，使得总容量最大呢？显然，这是一个条件优化问题，应用拉格朗日乘子法（Lagrange Multiplier）可以得到最优解，该最优解通常称为注水定理（Waterfilling Theorem）。本书暂时不具体讲拉格朗日乘子法，注水定理最后功率分配策略的趋势是，噪声P_N（f）小的频带，信号功率P_x（f）多分配一些；反之，噪声P_N（f）比较大的区域，P_x（f）少分配一些，甚至不分配，如图11-4所示。看起来也比较直观，同样多的功率分配给噪声高的地方显然性价比低，不如给噪声低的地方多分一点。

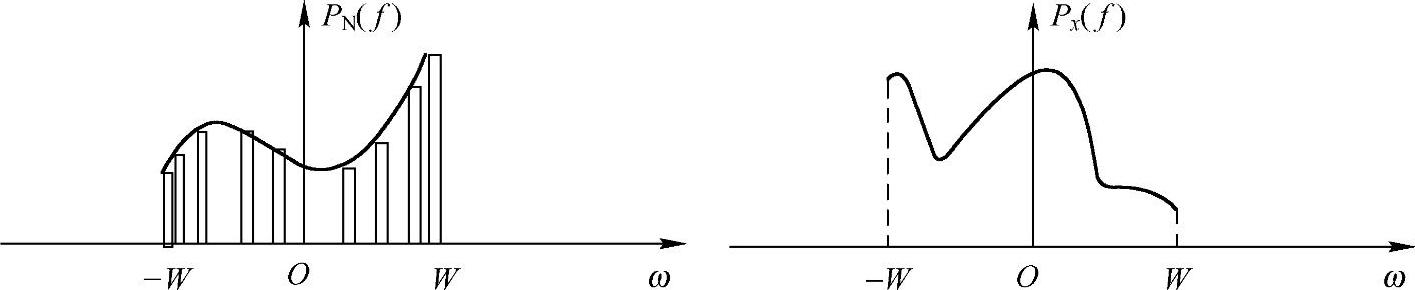
图11-4 注水定理噪声功率分布与信号功率分配关系

特别地，对于AWGN来说，P_N（f）处处相等，按照注水定理，最优的功率分配方法就是平均分配功率。也就是说，达到AWGN信道容量的信号的功率谱也是常数，差不多隐含了达到AWGN信道容量的信号也为高斯白噪，即随机码。

除了拉格朗日乘子法，我们再从另一个角度来看为什么最佳功率分配满足注水定理。首先，划分成平行信道后，总容量为

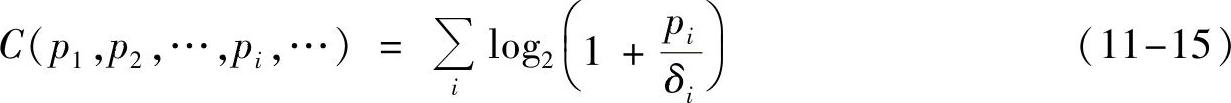
其中，p_i，δ_i分别为第i个子信道的信号功率和噪声功率。式（11-15）对p_i求偏导，得

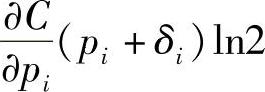
请回忆导数的意义，导数的大小表示自变量增加一点带来的函数值变化快慢。可以想象，最佳功率分配后，要使得所有p_i对应的导数相等。否则，把导数小的信道的功率转移到导数大的信道总是能使得总信道容量增大，因为相同功率能使导数大的信道容量增加更多。既然最后要求p_i+δ_i^一样，那么显然δ_i越小，得到的信号功率p_i越多；反之，噪声功率（密度）δ_i越大，得到的信号功率越少，甚至没有。

回忆我们讲过的I/Q调制。假设发射端采用I/Q调制来发送信号，在I路发送f₁（t），在Q路发送f₂（t），最后发射出去的信号为

s（t）=f₁（t）cos（ω_ct）-f₂（t）sin（ω_ct）（11-16）

经过AWGN信道后，接收端收到信号(www.xing528.com)

接收端再把信号s～（t）还原成基带信号，得到的I/Q两路信号分别为

其中，一般情况下，ω_I（t）和ω_Q（t）是功率相等但独立的高斯白噪声。如果把发射端信号写成复基带信号f（t），即

f（t）=f₁（t）+jf₂（t）（11-20）

把接收端信号写成复基带信号，则

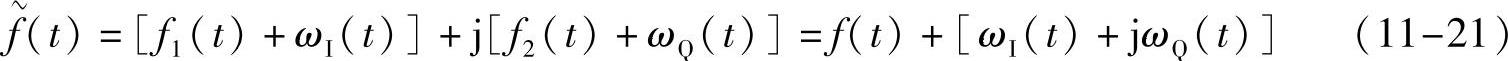
我们可以把ω_I（t）+jω_Q（t）称为复高斯白噪声，这样的信道称为复高斯白噪信道。

三言两语

还记得我们讲I/Q调制时，留了一个问题：当I/Q两路都可用时，两路都用比只用一路更高效吗？注水定理已经给出了答案。假设发射端不管是否I/Q两路都用，提供的总功率是一定的。而信道是复高斯白噪信道，现在是否I/Q都用，等价于是否两路都分配功率的问题。我们知道I/Q两路是可独立区分的，那么复高斯白噪信道的信道容量等于I/Q两路的信道容量之和。注意到I/Q两路的噪声功率相等，那么根据注水定理，想提高信道容量最好两路平分信号功率，而不是把功率集中在一路上。信道容量提升了，当然效率高了。

由以上讨论，假设复高斯白噪信道I/Q两路的功率分别都为σ²/2，称该信道为功率为σ²的复高斯白噪信道。那么，我们可以得到复高斯白噪信道下的信道容量。

定理11-3 对于功率为σ²的复高斯白噪信道，假设信号带宽为W，总功率为P，那么该复高斯白噪信道的信道容量C（单位：bit/s）为

如果换成信道容量（单位：bit/symb），则有

证明 因为最佳功率分配（即平分）时，I/Q两路的信道容量（单位：bits/s）分别是

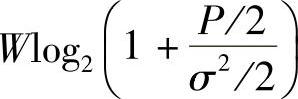
相加即得复高斯白噪信道下总信道容量（单位：bit/s）。信道容量（单位：bit/symb）类似，得证。