延续有失真系统无失真通信技术

现在，我们要应用有失真系统的无失真通信的一些结论。考虑这么一个具体的问题：X序列中的元素集合为实数域RR，概率密度函数为f（x），方差为S，在AWGN信道下，信道容量是多少呢？

假设AWGN噪声w均值为0，功率为σ²，即w～（0，σ²）。任何信号x，x∈RR经过信道后，接收端收到y=x+w。要用式（11-1）计算信道容量，首先我们要看转移概率是多少。

假设发送端发送的是x，经过信道得到y的概率P（y|x）是多少？首先需要明确一个事实，噪声w是连续的，因此y也是连续的，可以取到任何实数。再因为发送x，并且x和w独立，从而要得到y，只能是高斯噪声w的取值为y-x。那么y出现的概率就是w=y-x出现的概率，即

P（y|x）=P（w=y-x）（11-7）

因此，对于某个固定的x来说，接收到y的分布Y_x是均值为x的高斯分布Y_x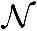～（x，σ²）。但是，请注意反过来一般不一定成立。即给定y时，x的分布P（x|y）并不一定是高斯分布。比如，x只取几个离散值。显然，对于这几个离散值之外的某个x₀，它出现的概率为0，并不是

P（x₀|y）=P（w=y-x₀）≠0（11-8）

从实质来说，这是因为y和w并不是相互独立的。对于某个固定的y来说，w能不能取某个数w₀，并不是独立的，取决于x能不能取到y-w₀。

接着，因为有了条件概率P（y|x），从而可以计算条件熵，

也就是说，不论X服从什么分布，H（Y|X）总是一定的。那么，要使H（Y）-H（Y|X）最大，只需要H（Y）最大就好了。

可以看到，这里将Y的取值范围限制在RR内，方差为(www.xing528.com)

Var{X}+Var{w}=S+σ²（11-10）

而我们刚开始讲熵的概念时，已经知道当Y在这些限制下服从高斯分布时，其熵H（Y）最大，最大为

因此，我们得到该AWGN（每符号时间内）信道容量（单位：bit/symb）为

由我们前面讲的高斯变量有限分解定理6-3可知，当达到信道容量时，X和ω独立，ω和Y都为高斯分布，那么X一定也为高斯分布。

总结上面的讨论，现在假设发射端是功率受限的，具体X的功率限制为P，当X也满足高斯分布时，在某给定AWGN下达到其每符号时间内信道容量，该信道容量（单位：bit/symb）为

三言两语

再仔细分析一下，这里离散情况只说明了：如果能够把X序列传输到接收端，接收端收到的序列仅为发送端发送的X序列中每个元素叠加了一个独立的高斯噪声，则一个X序列中元素（每符号）平均携带的最大信息量为C比特。当然，如果接收到T个这样的元素，携带的信息总量大概为TC比特。

上面仅是离散情况的推导，是一个逻辑上的结果，没有同模拟信号和现实时间概念^[1]联系起来。接下来，我们想办法转化为模拟信号的情况，看单位时间（每秒）内能无误传输的最大信息量是多少。