几何模型化的有趣应用探索

11.1.3节关于香农容量公式的推导里，给定AWGN信道和提供的信号功率，从几何模型来看，只要合适地选择一个信号集合，以这些信号点为中心，噪声功率为半径的小球两两不相交，那么则能实现无误传输。反之，如果信号集合选得不合适，则使得有些球之间出现相交的情况，一定可能有错误的传输。那么所有小球出现相交情况的多少以及每次出现的相交严重程度，决定了发生错误概率的大小，相交情况越多越严重，错误概率就越高，反之错误概率越小。

根据这些定性的思考方法，我们可以做一些应用如下。

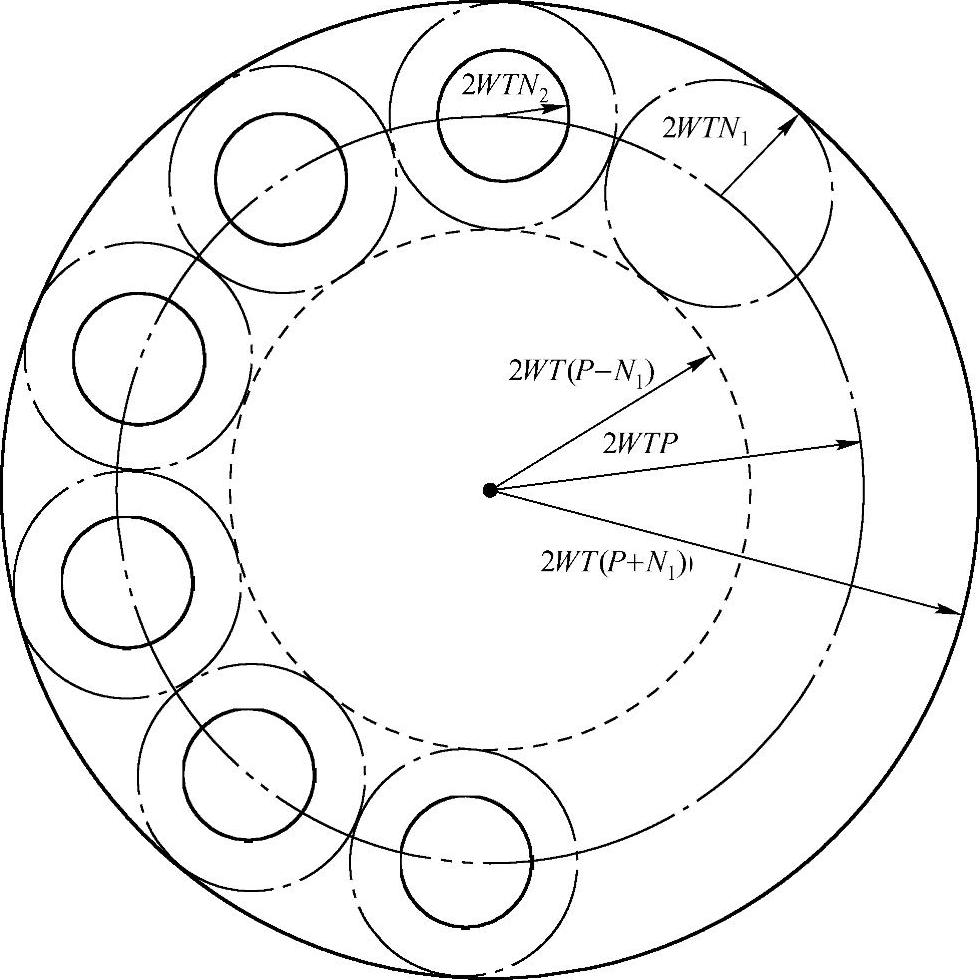
图11-2 噪声大时能无误传输保证噪声小时一定能无误传输

1.功率相同，噪声不同

现在假设有两个AWGN信道，信号功率都配置为P，但噪声功率分别为σ²₁，σ²₂，其中σ²₁≥σ²₂。

显然，一个信号集合S中的信号在σ²₁信道上能无误传输，那么在信道σ²₂上也一定能无误传输。根据上面香农容量推导知，以S中信号为中心，σ²₁为半径的大球之间都不相交，显然以σ²₂为半径的小球也不相交。如图11-2所示，其中N₁=σ²₁，N₂=σ²₂。但反之不成立，即一个信号集合S中的信号在信道σ²₂上对应的球不相交，但对于信道σ²₁来说，这些球可能出现相交的情况。

根据这个逻辑更进一步，更现实的问题，同一编码调制方式出来的信号，以这些信号为中心对应的小球在σ²₁信道上的相交程度必然大于在σ²₂信道上的相交程度，从而在信道σ²₁上的误码率必大于σ²₂信道上的误码率。(www.xing528.com)

2.功率不同，噪声相同

现在假设同一个AWGN信道，噪声功率为σ²，但信号功率分别为P₁，P₂，其中P₁≥P₂。

显然，一个功率为P₂的信号集合S中的信号在该AWGN信道上能无误传输，那么S中每个信号乘以一个功率缩放因子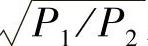后得到的信号集合S＇，也能在该AWGN信道上无误传输。原因很简单，根据上面香农容量推导知，球的大小没变，相对位置没变，只是球心移了位置！如图11-3所示，其中N=σ²，里面一圈小球往外挪后，仍然不相交，并且相互之间距离可以更大。但，反之不成立，即不相交的大圈往里挪不一定仍然不相交。

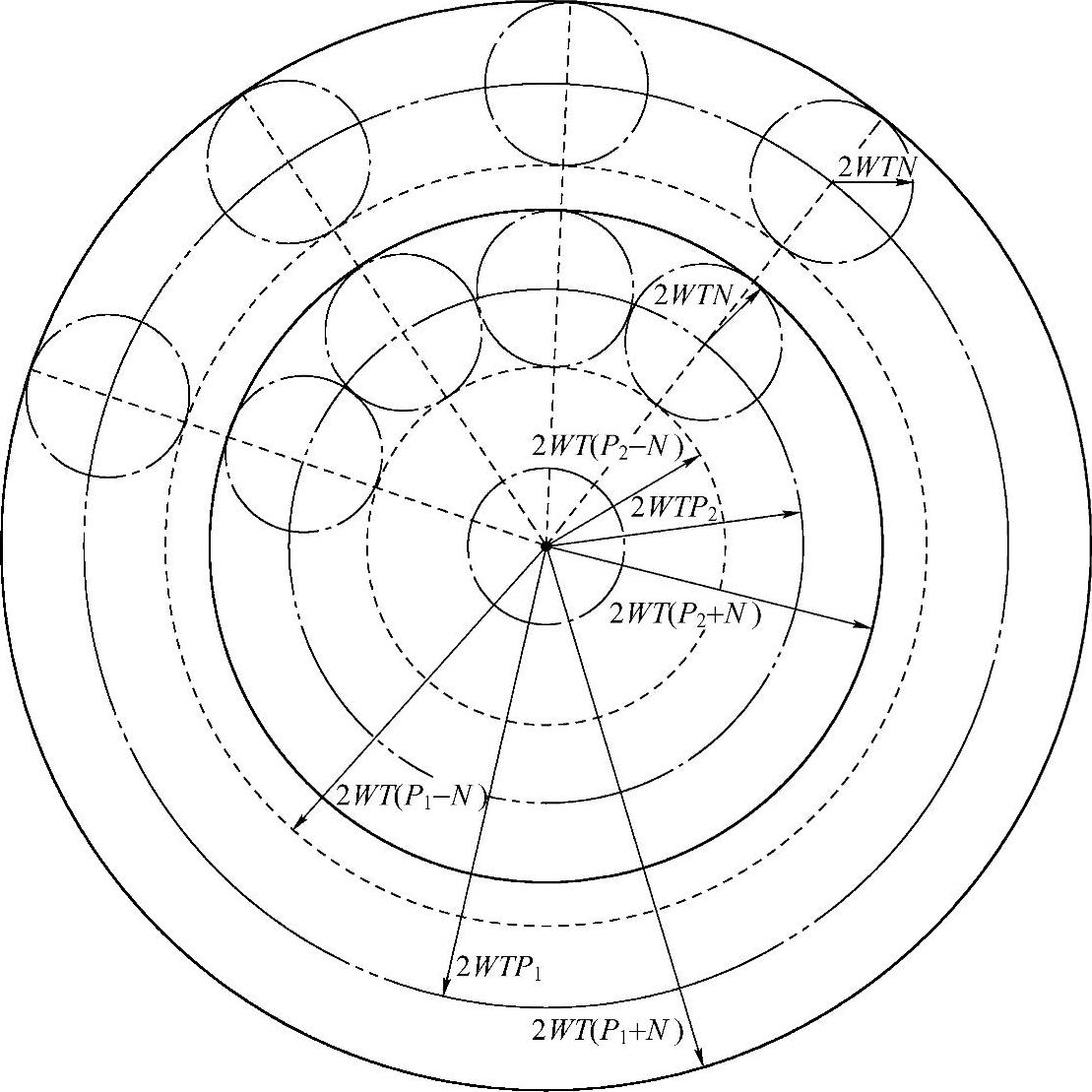
图11-3 功率小时能无误传输保证平移后仍然能无误传输

另一方面来说，如果信号集合S中的信号对应的球相交，那么加大功率后的信号集合S＇中的信号对应的球相交的程度会减轻，甚至达到不相交。根据这个逻辑更进一步，更现实的问题，同一编码调制方式出来的信号，以较大功率发送这些信号（S＇）的误码率会比用较小功率发送这些信号S的误码率低。

除了这两个应用外，更多的问题也可以通过这个集合模型来找到直观的解释，请读者朋友自己去思考。