如何计算AWGN信道容量？

好啦，现在只要任何两个球面不相交，那就能区分两个点了。显然，球面不相交，必然整个球体也不相交。共有多少个能区分的原信号点就是看共有多少个这样不相交的球。如何计算到底有多少个不相交的球体个数呢？

再观察一下，因为最后经过噪声污染后的点离坐标原点最远处为半径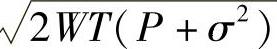的球面上，离坐标原点最近处为半径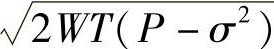的球面上。从而如图11-1所示，其中N=σ²实际上这些球都集中在离半径为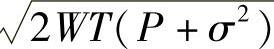的大球的表面很近那一圈上（球环上）。那么大球环上能装的不相交小球个数，可以看成半径为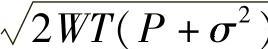大球里能装的球体与半径为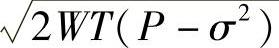大球里能装的球体个数之差。

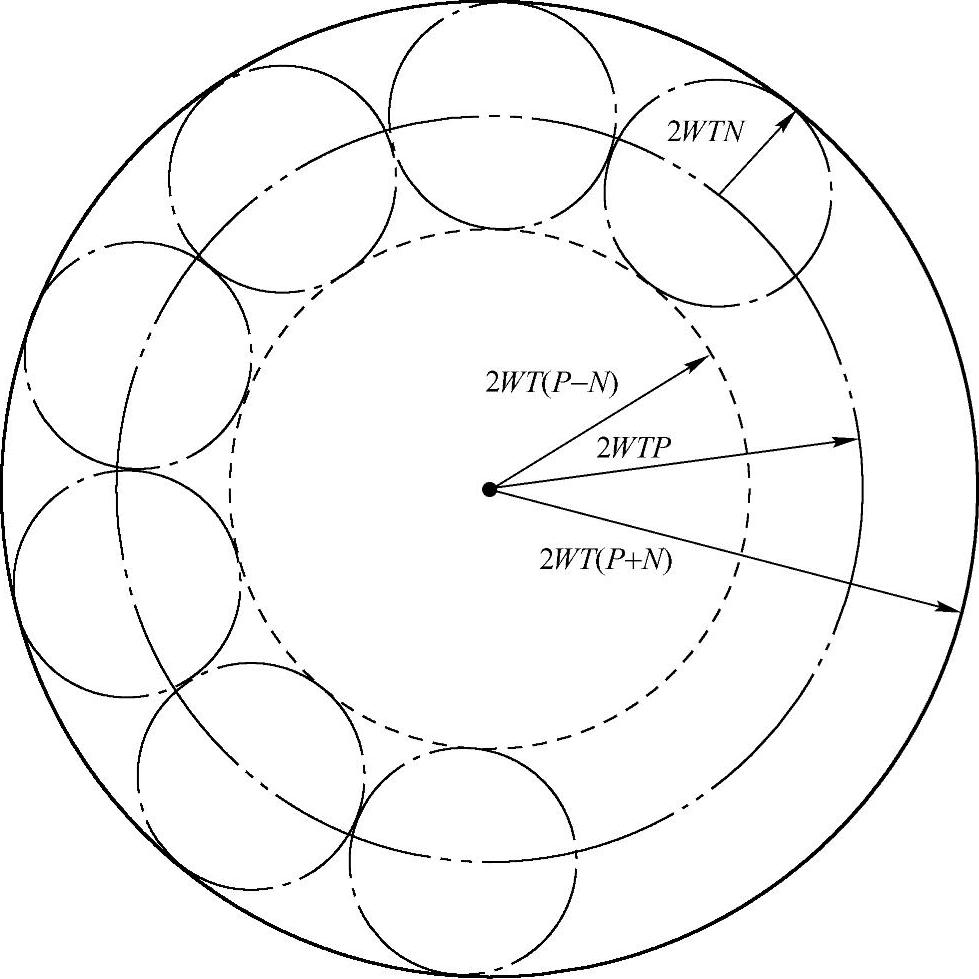
图11-1 大球环里不相交的球个数决定信道容量

根据广义球体容积计算公式，我们知道维数为n，半径为R的广义球体容积为

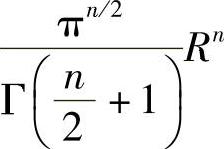
其中，分母Γ（x）为Gamma函数。其实我们只需要知道广义球体维数n相同时，容积与Rⁿ成正比就可以了，管它是什么函数。那么，我们可以得到球的个数（取对数后）为

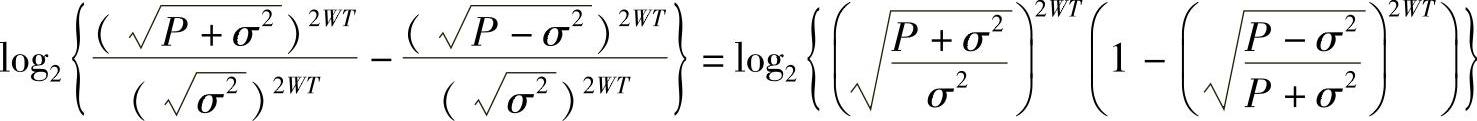
因为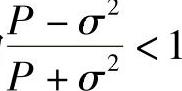，那么当T→∞时

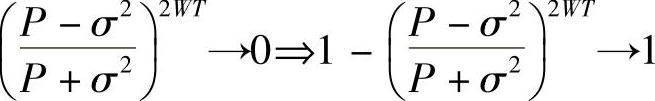
则当T→∞时，球的个数（取对数后）为(www.xing528.com)

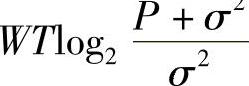
也就是说可以在时间T内无误传输这么多比特，即单位时间内信道容量（单位：bit/s）为

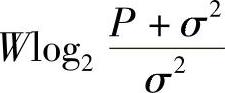
三言两语

假设有信息，即一些（事件）状态要传输，那么只要将每个状态对应一个如上不相交的点对应的信号发送，经过信道传输后，接收端能完全无误地识别出发射端发送的是哪个信号，从而可以对应知道该信号携带（承载）的信息。

根据上面讨论，就可总结得到大名鼎鼎的香农容量公式。

定理11-2（香农容量公式） 在AWGN信道下，若带宽为W，噪声功率为σ²，信号功率为S，则该AWGN信道下单位时间（秒，s）最多能无误传输的信息量，即AWGN下信道容量（单位：bit/s）为

注意这里的单位时间为每秒，和式（11-1）的单位时间每个符号（持续）时间略为不一样，它们之间的联系我们稍后再讲。