模拟信号的直观几何模型化方法

香农在1948年（包括1949年的“噪声信道下的通信”）开山之作中采用了直接看模拟信号区分度的方法。假设发射端可能信号x（t）带宽为W，功率为P。AWGN信道下高斯白噪声ω（t）功率为σ²，均值为0。在时间T内，共有多少个满足条件（带宽、功率限制）的信号在叠加完噪声后仍能两两区分开呢？所谓能两两区分开，指的是两个不同信号叠加完噪声后仍然不同。特别地，若噪声功率为0，则相当于没有噪声，当然任何两个信号都可以区分开。

我们知道，任一带宽为W，时长为T的信号f（t）可以由2WT个采样点来表示（特殊情况的微小误差暂不考虑），记采样点序列为{x₀，…，x_2WT-1}。不妨设这里是刚好以奈奎斯特率采样，则根据坐标与模的关系推导出采样点的平方和与该信号的功率的关系为

从而带宽为W，时长为T，功率为P的所有信号即对应所有长度为2WT且平方和为2WTP的采样点序列（向量），该向量在2WT维空间中对应以坐标原点为球心，半径为2WTP的广义球体（狭义球体仅为三维）球面上一点。

每个这样的信号经过AWGN后，其对应的采样点序列中每个采样点独立地叠加了一个独立同分布的高斯噪声，记叠加的2WT个高斯噪声点为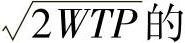(www.xing528.com)

{w₀，…，w_2WT-1}，xi→x_i+w_i另一方面，我们根据维纳-辛钦定理已推导知，高斯白噪声的功率即为每个时刻对应的高斯变量的方差，则每个采样点独立地叠加了一个均值为0，方差为σ²的高斯噪声，即w_i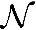～（0，σ²）。从整个采样点构成的向量来说，经过AWGN后变成了另一个向量[y₀，…，y_2WT-1]

[x₀，…，x_2WT-1]→[y0，…，y2WT_-1]=[x0+w0，…，x2WT_-1+w2WT_-1]（11-3）向量[y₀，…，y_2WT-1]在2WT维空间中所对应点距离原信号点[x₀，…，x_2WT-1]为

想一想，如果不同信号对应的采样点向量经过AWGN后得到的相应向量能够两两区分开，那么原信号就可以两两区分开。问题是什么时候能两两区分开，能区分多少呢？下面接着讨论。