无误通信的秘诀：探索可能性

先说，如果X序列是有限长的，那么任何一个X序列经过信道后，可能得到任何Y序列，也就是转换概率P（y_j|x_i）在有限情况下基本没什么用，此时无论如何都不可能实现无误判断。所以，在有概率的情况下，我们如果还想得到比较确定的判断，就必须先让概率的随机效果达到稳定状态，也就是要用到大数定理使其收敛于确定效果。

既然如此，我们就假设X序列是无限长的，长度为T→∞。那么根据大数定理，任何一个这样的X序列中，x_i的个数必然有TP（x_i）个。但请注意，大数定理只能保证x_i出现的个数，并不能保证x_i在X序列中出现的位置。也就是说，任何满足x_i的个数为TP（x_i）的序列都是等概出现的。那么，这样的X序列共有多少个呢？这就是一个简单的组合问题，即从T个位置中选出TP（x_i）个位置放上x_i。可以先从T个位置中选TP（x₁）个位置放x₁，再从T-TP（x₁）个位置中选TP（x₂）个位置放x₂，依此类推，最后根据9.1节关于熵的讨论得到序列总个数为

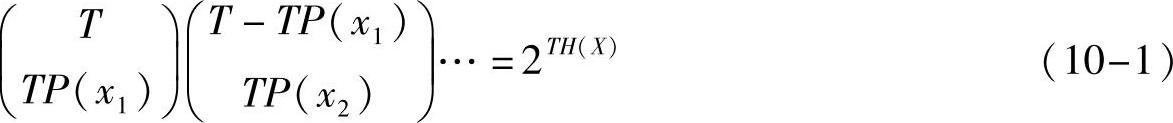
其中，H（X）为分布X的熵。

再考虑任何一个这样的X序列经过信道后，接收端能得到多少个不同的Y序列呢？还是一个组合问题。注意，当T→∞时，X序列中x_i的个数TP（x_i）也是无限长的，所以根据大数定理，经过信道后必然有TP（x_i）P（y_j|x_i）个x_i变成了y_j，但到底是哪一个x_i变成了y_j不确定。和上面相同的计算方法，单看X序列中某个x_i所在的TP（x_i）个位置经过信道变成y_j的不同情况有

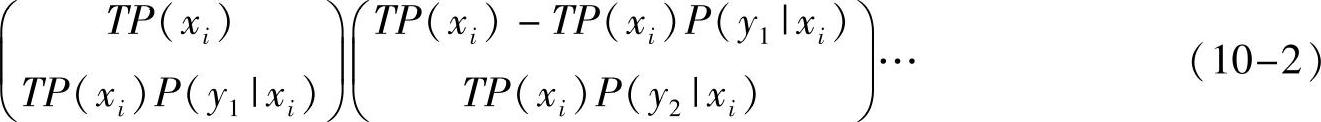
如图10-1所示，这些不同情况必然对应得到不同的Y序列，再联合看所有x_i，计算得到任何一个X序列经过信道后可能变成的不同Y序列个数为

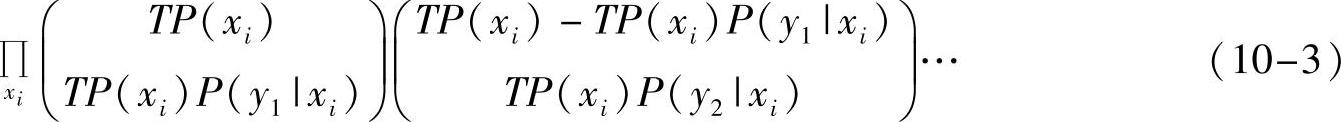
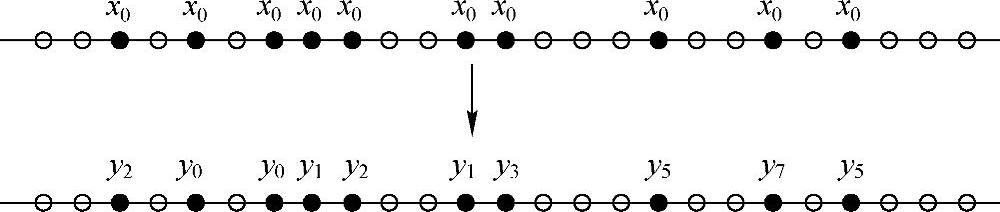
图10-1 X序列经过信道后元素转移情况

现在回到最开始的问题：怎么从接收到的Y序列来无误判断发射端发送的是哪个X序列呢？

从前面的分析计算，我们可以看到可能会有两个不同X序列经过信道后得到同一个Y序列，显然通过这样的Y序列是不能无误判断出发射端发的是哪一个X序列的。因此要无误判断，首先就得无误区分得到的Y序列是哪一个X变过来的；要无误区分，就要求两个X序列经过信道后得到的Y序列没有交集。那么，接下来归结为讨论如下两个问题：

●存在性。是否能找出两个不同X序列经过信道后的Y序列没有交集呢？

●极限能力。进一步，最多能找出多少个不同X序列，使得它们经过信道后得到的Y序列两两都没有交集呢？(www.xing528.com)

针对这两个问题，如果序列个数是有限的情况，可以画一个二分图或者穷举来看看。但这里是一个无限的比较泛的命题，此法不可取。这里，我们介绍一个概率方法，这种概率方法的思想可以应用到任何关于存在性问题的讨论里。上面的两个问题可以另外叙述成：是否存在2T^R个X序列，它们两两对应的Y序列没有交集呢？R最大为多少？

概率方法思想 概率方法的思想是：构造一个合理的概率空间，使得要讨论的命题为该概率空间里的一个事件，要证明该命题是可能成立的（存在的），只需要证明其对应事件在概率空间上的发生概率大于0即可。

通过分析，可以得到如下非常重要的结论：

定理10-1 对任意的R>0，当R<H（X）-H（X|Y）时，可以找到2^TR个X序列使得这些序列经过信道后得到的Y序列各不相同。

更不可思议的是，如上定理中“找到2^TR个X序列”的方法之一就是从所有序列中随机等概率地独立选择2^TR个X序列。也就是说，从所有X序列中随机等概率地选择2^TR个X序列，那么这些序列经过信道后得到的Y序列几乎各不相同。

既然存在这样2^TR个序列，当发射端发射这2^TR个X序列时，接收端可以根据接收到的Y序列无误判断出发射端发射的是哪一个X序列，那么这2^TR个X序列可以用来作为表示某组消息的信号，并能实现无误通信。且此时，单位时间（每个符号时间）内平均能无误传输的比特速率为

另一方面，我们知道这样的序列个数2^TR有最大值，说明在该信号表示方法及相应信道下，能无误通信的消息个数也有这个最大值

2^TR≤2^T[H（X）-H（X|Y）]（10_-5）

即信道平均能无误传输的比特速率（每个符号时间携带比特数）有最大值

R≤H（X）-H（X|Y）=I（X；Y）（10-6）

再一方面，假设信道的转移概率P（y_j|x_i）不变，即转移概率只是信道的固定特征，和输入分布无关。我们把X序列的集合改变了，即把P（x_i）改变了，那么这个能区分的最大序列个数也会相应改变。那么遍历所有可能的分布P（x_i），其中能区分最多序列的那一个分布P（x_i）能表示且无误通信的消息个数最多。后续，我们知道这就是所谓的该信道的容量。