数据压缩极限：熵的重要应用

9.1节香农熵的推导，还可以得到如下形式描述的命题。

性质9-2（数据压缩极限定理）集合{x₁，x₂，…，x_N}，对于由该集合中符号组成，且符号x_i出现概率为p_i的所有消息，若要对这些消息进行二进制编码，那么每个符号平均至少需要的比特个数为

数据压缩极限定理只是从理论上说明了最小平均要用多少比特来编码一个序列，但是没说具体怎么编。当然从理想情况来说，它其实也说了怎么编，即把所有可能的无穷长序列摆在哪儿，然后看总共需要多少比特，最后每一个序列对应一个总共比特数的一种取值就好了。

但问题是，要等到无穷长序列出来了才开始编，是不现实的。现实可以想到的总是以一个有限长为粒度，将无限长序列分割成有限长的一部分再编码，然后再把各有限长部分对应的编码拼起来得到无穷长序列对应的编码。而所谓“有限长”，最自然最简单的情况就是把组成序列的每一个可能的符号都用比特来分别编成二进制。可以想象，这种编码方法最后需要的比特数肯定比数据压缩定理说明的极限情况多。比如最笨的方法，假设共有N=8个数据符号，不管每个符号出现的概率是多少，每个就用3比特表示就好了，即平均每个符号需要3比特表示。

有哪些比较好的，与极限情况差别较小的编码方法呢？我们比较熟悉的哈夫曼（Huff_- man）编码方法就是一个，下面简单介绍以二叉树结构来生成哈夫曼编码的过程。

假设有符号{x₁，x₂，x₃，x₄，x₅}，分别对应的概率为

{0.1，0.2，0.2，0.15，0.35}

先找到其中概率最小的两个x₁，x₄，把它们作为一个树叉的两个叶子，树叉根点s₁的概率为两个叶子概率之和0.25；在{s₁，x₂，x₃，x₅}中继续找概率最小的两个x₂，x₃，把它们作为一个树叉的两个叶子，树叉根点s₂的概率为两个叶子概率之和0.4；在{s₁，s₂，x5}中继续找概率最小的两个s₁，x₅，把它们作为一个树叉的两个叶子，树叉根点s₃的概率为两个叶子概率之和0.6；在{s₂，s₃}中继续找概率最小的两个s₂，s₃，把它们作为一个树叉的两个叶子，树叉根点s₄的概率为两个叶子概率之和1；最后把二叉树里每个分叉的两条边分别标上0和1，每个x_i的编码就是整棵二叉树根到x_i的边上的0，1序列。具体过程如图9-1所示。

最后，各符号的二进制表示为(www.xing528.com)

x₁=101，x₂=01，x₃=00，x₄=100，x₅=11

那么，每个符号平均需要的二进制比特数为

3×0.1+2×0.2+2×0.2+3×0.15+2×0.35=2.25（9-13）

而极限情况需要的最小比特数为

如果采用最笨的方法，则每个符号需要log₂5≈2.32比特表示。可看到哈夫曼编码和理论极限已经很接近了。仔细观察知，最笨的方法是等长编码，即每个符号采用相同的比特数来表示；而哈夫曼编码是不等长编码，其主要思想就是出现次数多（概率大）的符号用较短的比特序列表示，而出现次数少的符号用较长的序列表示。数据压缩属于信源编码领域，计算机里各种压缩文件都采用了一定的数据压缩方法，比如ZIP文件等；各种图片格式（JPEG、BMP等）也都采用了一定的数据压缩方法。

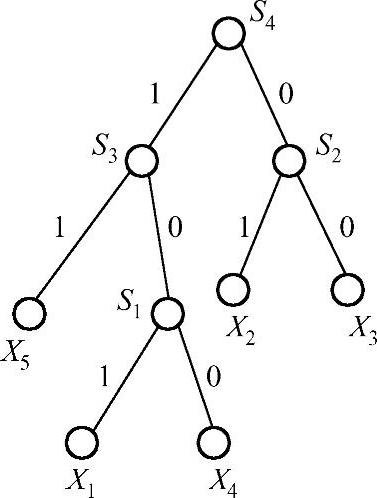
图9-1 二叉树生成哈夫曼编码