通信新读：探讨乘性噪声的影响

下面看看若不是加性信道，而是乘性信道，情况会怎样？我们假设信号X经过信道后得到Y，有

Y=WX

其中，W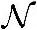～（0，σ²）。若仍然按先验/后验判决准则来判断，则先计算后验概率，得

若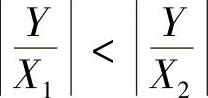，即X₁>X₂，则

P（X₁|Y）>P（X₂|Y）

那么X₁出现的概率大。可以看到，后验概率判决时，和接收到的Y没关系，和噪声功率也没关系，仅与发送的数据的绝对值大小有关。

我们再看看错误概率是什么状况。若X₁>X₂，则不论发送的是什么，总是被判成X₁。显然X₁的错误概率是0，而X₂的错误概率为100%。此时平均错误概率为

P（X₁）0+P（X₂）1=P（X₂）(www.xing528.com)

则绝对值相对小的X₂出现的概率越大，最后的平均错误概率越大。

如果X₁=X₂该怎么处理？比如，满足关系X₁=-X₂，例如BPSK、QPSK符号？假设X₁、X2等概出现。有什么好的办法吗？好像没有。若我们固定总是挑其中一个作为判决结果，那和上面的一样，一个错误概率为0，另一个为100%，平均错误概率为50%。若不固定挑，每次以50%的概率随机挑一个呢？最后的平均错误概率也为

50%×50%+50%×50%=50%

事实上，若是随机猜，不论X₁、X₂是否等概分布，平均错误概率都是50%。也就是说，上面的例子中采用后验概率判决时，若绝对值较小的X₂出现的概率大于50%，那么平均错误概率会大于50%，还不如随机猜。

三言两语

可以看到，随机猜，表面给人感觉不太科学，事实上有时它已足够科学了。