最小化平均错误概率的判决方法

8.1.3节讲的先/后验概率判决准则虽然看起来合理，但是不能保证实际性能最好。例如，发射端两个信号出现的概率分别为P（X₁）=0.01%，P（X₂）=99.99%，可以想象最简单的判决方法是总判成X₂。虽然X₁总是被判错了，但它出现的概率本来就很小，故总体上的错误概率很小。而若按照上面的方法来判决，则可能有一部分的X₁被判正确了，但X₂可能有很大一部分被判错了，得不偿失。

所以，先/后验判决虽然看起来比较公平，但是整体实际性能并不好。基于上面的考虑，我们考虑另外一种标准：平均错误概率最小化。

以8.1.3节的例子为例，平均错误概率为

P_e=P（X₁）P_X1（X₂）+P（X₂）P_X2（X₁）（8-18）

注意到，先/后验概率方法最后实际可以转化成用接收到的数据和门限（X₁+X₂）/2比较，来判断发送的是X₁还是X₂。若以同样的思想，我们把门限换成另一个，相应地错误概率P_X1（X₂）和P_X2（X₁）都会发生变化，如图8-7所示，从而平均错误概率P_e也会发生变化。例如，若门限换成T，则错误概率变成

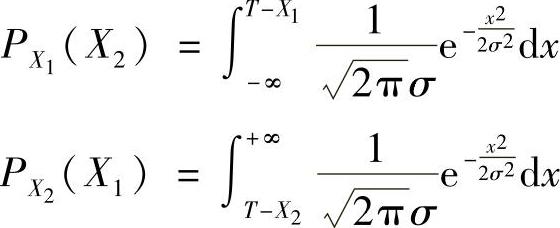(www.xing528.com)

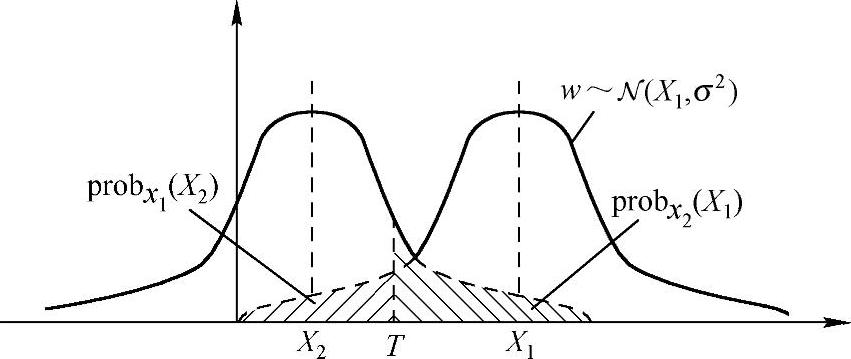
图8-7 判决门限改变导致平均错误概率改变

在该门限判决思想下，总存在一个门限T，使得平均错误概率最小。最后把接收到的数据和这个门限比较来判决，一定能使得平均错误概率最小。

具体地，使得平均错误概率最小的门限是多少，与发射端可能信号各自的出现概率以及高斯噪声功率有关，需要具体情况具体计算，此处就不统一处理了。