先验概率和后验概率的判决

1.信号判决法则

接下来，大家看如下的判决方法：在接收到数据的条件下，这个接收数据最有可能是因为发射端发射哪个信号造成的，就认为发射端发射的是哪个信号，这个可能性称为后验概率，这个判断准则就是根据接收到的数据，判断成后验概率最大的，我们称之为后验概率准则；或者看发射端在发射哪个信号的条件下，经过AWGN信道后接收到数据的概率最大，这个条件概率称为先验概率，这个准则称为先验概率准则。可以看到这两个判决准则感觉比较直观又很合理，这一节我们就来讨论它们。这两个准则理论上既可以用于模拟（意义）信号的判决。也可以用于数字信号的判决。但为了在讨论过程中，方便给出一些量化的结果，我们仅讨论用于数字信号的情况。

首先，这两个说法似乎表达的意思差不多，实际上还是有些区别的，取决于接收端是否提前知道发射端可能的发射数据集合。对于接收端来说，在发射端发射的数据的可能取值已知的情况下，先验概率和后验概率是相等的。下面以发射端只可能取两个值x₁和x₂来说明。首先，对于高斯噪声为w～（0，σ²）的AWGN信道，发射端发射一个数据x，接收端能接收到的数据也满足高斯分布，即以x为均值，方差仍然为σ²的高斯分布，

y=x+w～（x，σ²）（8-10）

从先验概率来说，如果发射端发射的是x₁，经过AWGN得到y，则高斯噪声w=y-x₁，即发送x₁能得到y的概率就是AWGN中高斯噪声w=y-x₁的概率；发射端发射x₂的情况类似。则先验概率为

prob（y|x₁）=prob（w=y-x₁），prob（y|x₂）=prob（w=y-x₂）（8-11）

从先验判决准则来说，上面两者谁大，就判断成发射端发射的数据。

从后验概率来说，接收端已经得到y，如果是因为发射端发的x₁才得到的y，高斯噪声必然有w=y-x₁；发射端发射x₂的情况类似，则后验概率为

prob（x₁|y）=prob（w=y-x₁），prob（x₂|y）=prob（w=y-x₂）（8-12）

同样，从后验判决准则来说，上面两者谁大，就判断成发射端发射的数据。显然，先验概率和后验概率相等

prob（x₁|y）=prob（y|x₁），prob（x₂|y）=prob（y|x₂）（8-13）

对于这种情况，按先验判决和后验判决出来的结果是相同的。

对于AWGN来说，上面的先验与后验判决准则，除了可以从概率数字上计算来判决外，还有其他更直观的角度来描述吗？这个可以有。我们前面讲过，对于均值为0的高斯噪声有个性质：瞬时噪声取值绝对值较小的可能性较大。这就说明发送一个数据符号，在接收端接收到的值离它较近的概率较大；反过来说，接收端把接收到的值，判决成离它较近的可能数据符号，这种判决方式是正确的概率较大。我们把这种判决方式称为就近判决原则。

更一般地，对于均值为_μ，方差为σ²的高斯噪声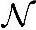（_μ，σ²），总是可以写成一个固定数μ与均值为0的高斯噪声之和，即

（_μ，σ²）=μ+（0，σ²）

那么，假设发射端发送的可能数据为x₁，x₂，经过该AWGN后，接收端接收到的数据为

x₁+μ+（0，σ²）

x₂+μ+（0，σ²）

相当于发射端发射的可能数据为x₁+_μ和x₂+μ，再经过了一个均值为0的AWGN信道（0，σ²）。这种情况下，就近判决方式具体为，看接收到的数据距离x₁+μ近，还是距离x₂+μ近。总之，非0均值AWGN可以很简单地转化为均值为0的AWGN来处理，后续我们就不会对这种情况分别描述，都只以均值为0的情况来讲解。

对于就近判决原则，除了比较距离之外，还可以进一步转化最后判决时依赖的形式。假设发送端的数据符号有两种：X₁和X₂，且X₁>X₂。接收端收到的是Y=X+W，其中X为二者之一，W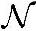～（0，σ²），即均值为0、方差为σ²的高斯分布。那么，发送端发送哪个符号时，接收端收到Y的概率大呢？计算如下：

prob（Y|X₁）=prob（W=Y-X₁） （8-14）

prob（Y|X₂）=prob（W=Y-X₂）（8-15）

可以看到上面的概率与X、Y的分布无关。我们前面说了，绝对值小的数据出现的概率大。那么，若

Y-X₁≥Y-X₂

即，则发送端发送的是X₂的概率要比是X₁的概率大，那我们就判断成X₂；反之，X₁的概率大，就判断成X₁。也就是说，我们最后的判决依赖的形式可以是跟某个门限值比，这里门限为。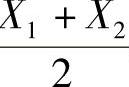

2.先验/后验判决性能(www.xing528.com)

既然是以概率判决，就不会绝对正确，那判断错误的概率又是多大呢？

首先，弄明白什么叫判断错误？判断错误这里就是，发送端确定发的是X₁，但我们用就近原则判断成了X₂。也就是说，如果发的是X₁，接收端收到的值仍然离X₂近，我们就会判断错误，发生这种情况的概率，就是我们按就近原则判断错误的概率，记为prob_X1（X₂），具体为

同样可以计算X₂被错判成X₁的概率为

图8-4 两两相互之间错误概率

我们知道积分就是求某个函数某个区间下覆盖的面积，这里函数是高斯分布函数，要求的面积就是阴影部分，如图8-4所示。由于高斯分布函数的对称性，我们知道上面两个错误概率公式所覆盖的阴影面积是相等的，也就是说，在就近判决原则下，两两相互之间判断错误的概率是相等的。

注意，这里是两两比较，而不是所有人比较。也就是说，如果发射端可能的发射信号只有两个，那么它们两两互叛错误概率相等，等价于说法“所有人被判决成其他人的错误概率相等”；然而当发射端可能的发射信号多于两个时，显然并不成立。比如，发射端有3个可能信号：X₁、X₂、X3，则prob_X1（X₂）不一定等于prob_X1（X₃）。但两两之间仍然具有对称性，即prob_X1（X₂）=prob_X2（X₁），prob_X3（X₂）=prob_X2（X₃）等。

进一步，如果高斯噪声功率固定，即求面积的函数曲线不变，而X₁和X₂的距离变大，即X₁^-X2和X2-X1一个变大一个变小，其各自覆盖的面积分别减小，即错误概率减小，如图8-5所示。

图8-5 信号距离增大，AWGN信道不变

反过来，如果X₁和X₂的距离固定，而高斯噪声的功率减小，则同样使得各自覆盖的面积减小，即错误概率减小，如图8-6所示，注意功率变小表现为概率密度曲线变瘦高。更进一步，X₁和X₂的距离变大，同时高斯噪声的功率减小，最后显然也使得错误概率减小。

图8-6 信号距离不变，AWGN噪声功率减小

从这些分析可以看出，当X₁、X₂给定时，相互判决错误概率仅与可能信号的距离X₁-X₂²和噪声功率σ²相关，并且它们之间的比值（X₂-X₁）2/σ²越大，错误概率越小。并且最后可以归纳为，错误概率与X₁、X₂的绝对取值和噪声功率的绝对取值无关，仅由比值确定。

通常，当可能信号欧氏距离一定时，我们想以较小的平均能量（功率）发送数据，即要X²₁+X²₂/2尽量小。分析表明，当X₁=-X₂时，是一个比较好的满足要求的选择。此时，

（X₁-X₂）2=4X²₁=4X²₂

而此时信号的平均功率为

从而

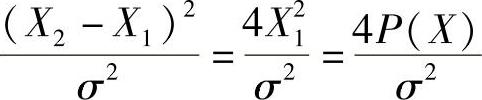
体现的就是信号平均功率与噪声功率的比值了，其中，P（X）表示信号X=X₁或X₂的平均功率，也就是经常说的信噪比（Signal to Noise Ratio，SNR）。

那么，上面的分析可以这样总结，按就近原则判决，信噪比（SNR）较大时，误码率低；反之，信噪比（SNR）较小时，误码率高。

思考一下 如果噪声并不是瞬时值小的概率大，还会用就近原则解调吗？还会追求经常强调的尽量提高SNR吗？