数字通信系统之相关接收

相关接收是接收端利用信号相关器和比较判决来确定发射端发射了哪个信号的方法，相关接收方法是少数的保有模拟意义的处理方法之一。其处理流程示意图如图8-1所示。

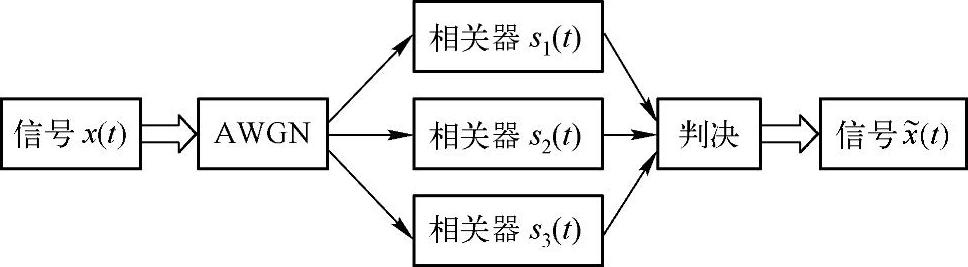
图8-1 相关接收判决

从流程图可以看到，在接收端需要有对应于各可能信号的相关器，用来与接收信号（经过信道的信号）做相关运算，然后比较各可能信号分支得到的相关运算值，用最大的分支相关器对应的信号作为发射端发的信号。

相关接收方法的原理利用了Cauchy-Schwarz不等式（参见本书附录A），假设发射端发射的所有可能信号的能量或功率相等，即

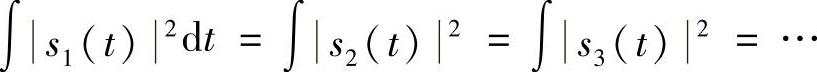
任意选取信号s₁（t）和所有可能信号做相关运算，该信号s₁（t）和自己做相关运算的值最大。(www.xing528.com)

当然，我们在附录A中的讲述并没有考虑噪声的影响，实际上把噪声考虑进来之后，结果也是类似的。只不过没有噪声时，信号与自己做相关运算是绝对意义上最大；而有AWGN时，信号与自己做相关运算是概率意义上最大。假设发射s₁（t），经过AWGN，接收端收到

y（t）=s₁（t）+w（t）（8-1）

其中，w（t）为高斯白噪声。接收信号y（t）与所有可能信号s_i（t）做相关运算，

最有可能和s₁（t）做相关运算得到的相关值y[1]最大。原因是一个信号s_i（t）和AWGN噪声w（t）的相关运算得到的值是一个高斯变量，并且只要多个信号s_i（t）的能量或功率相同，那么和同一个AWGN噪声w（t）的相关运算得到的值是几乎独立同分布的高斯变量。这和讲高斯变量时多个高斯变量的和类似，只不过相关运算涉及的积分是无穷和而已。因此，有AWGN与没有噪声两种情况的差别在于，前者是在后者的相关值上分别叠加了一个独立同分布的高斯噪声。这和在一堆参与比较的数之上，各自叠加一个公共的数而不会改变相互间大小关系类似，没有噪声时较小的分支如果叠加噪声后反而超过了之前较大的分支，就说明较小的分支所叠加的噪声变量取值很大，而根据高斯分布可知，噪声变量取值越大的概率越小。所以大部分情况下，还是没有噪声时较大的分支叠加噪声后仍然较大。

另一方面，我们可以看到，发射端有多少个可能的信号，接收端就需要准备多少个相关器，这说明相关接收方法虽然具有模拟意义，但只能用于数字通信系统，因为数字通信系统中发射端可能的信号数是人为设计的、有限的，也是接收端明确可以知道的。对于模拟通信系统，这个方法几乎没办法应用，因为模拟系统里发射端发的信号可以认为有无穷多个，那接收端也要准备无穷多个相关器才行，不现实！