探讨天生I路与Q路的区别

在上面对调制解调的基本思想介绍里我们还提到调制还有另外一个功能，就是把频率低的信号搬到频带高的部分，从而更有利于传输。不妨假设调制前的信号f（t）的频谱是以原点ω=0为中心的一个频谱。现在要把它的频谱挪到ω=ω_c处，一般的做法是用以ω_c为频率的正余弦信号和需要调制的信号相乘，从而实现频谱搬移。请回忆一下，正弦信号sin（ω_ct）和余弦信号cos（ω_ct）的频谱是在一对频点±ω_c处的冲激，仅方向不同。故由傅里叶变换的“时域乘积，频域卷积”知，任何一个信号乘以正余弦信号后的频谱为把原信号频谱分别向左搬移和向右搬移ω_c距离，然后再分别调整方向和幅度减半。图7-8中给出了一个用余弦进行频谱搬移的示意图。

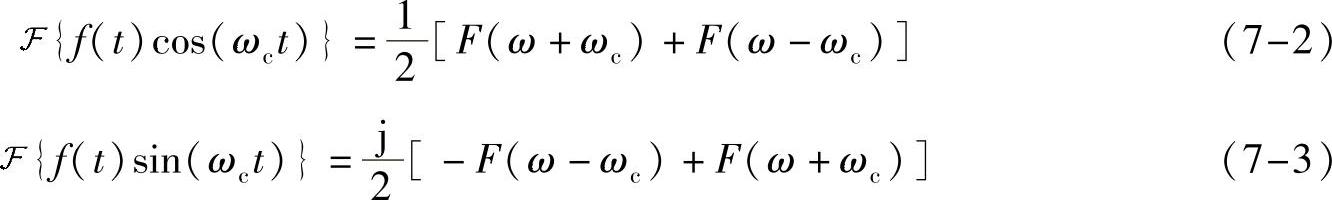
既然cos（ω_ct）和sin（ω_ct）都可以实现频谱搬移，如果用cos（ω_ct）和一个信号f₁（t）相乘，用sin（ω_ct）和另一个信号f₂（t）相乘，则把它们叠加起来的信号

s（t）=f₁（t）cos（ω_ct）+f₂（t）sin（ω_ct）（7-4）发出去，会怎么样？假设没有其他干扰噪声，理论上接收端可以唯一得到f₁（t）和f₂（t）吗？

我们知道，下面的操作可以还原f₁（t），即当ω_c大于f₁（t），f₂（t）的带宽时，用s（t）再乘以cos（ω_ct）并加个滤波器就可以得到f₁（t）。因为根据正余弦运算关系

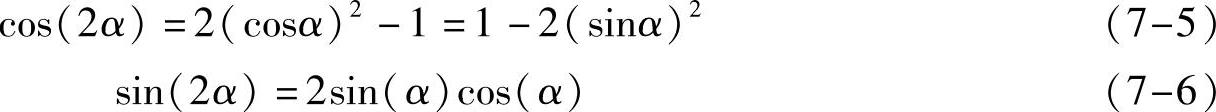
可知

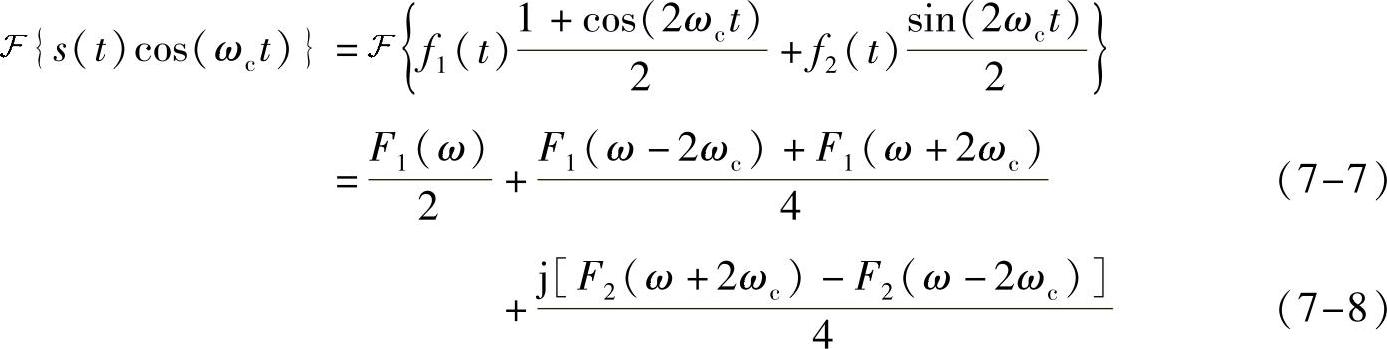
显然，只要加个滤波器把±2ω_c处频谱给过滤掉就可以得到信号f₁（t）了。整个过程如图7-9所示。当然，还有个系数差异，不过这个系数是固定的，且可以提前知道，无关紧要，再补上就行了。

类似地，用s（t）再乘以sin（ω_ct）并加个滤波器就可以得到f₂（t）

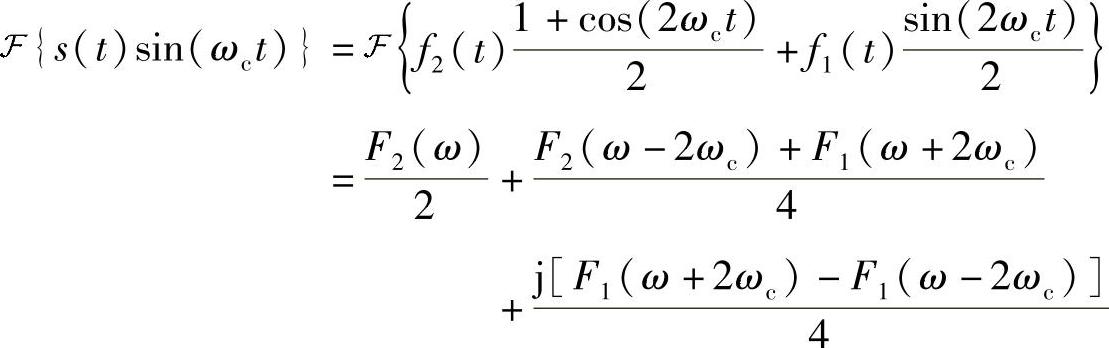
综合来看，接收端在接收到s（t）后，引出两个支路，其中一个支路和正弦信号相乘再滤波可以得到一起传输的其中一个信号（比如f₂（t）），另一个支路和余弦信号相乘再滤波可以得到一起传输的其中另一个信号（比如f₁（t））。

另外，上面提到要求ω_c大于f₁（t）、f₂（t）的带宽，如果不这样，则各频谱通过正余弦搬来搬去，最后会有重叠，没办法无失真还原，如图7-10所示。

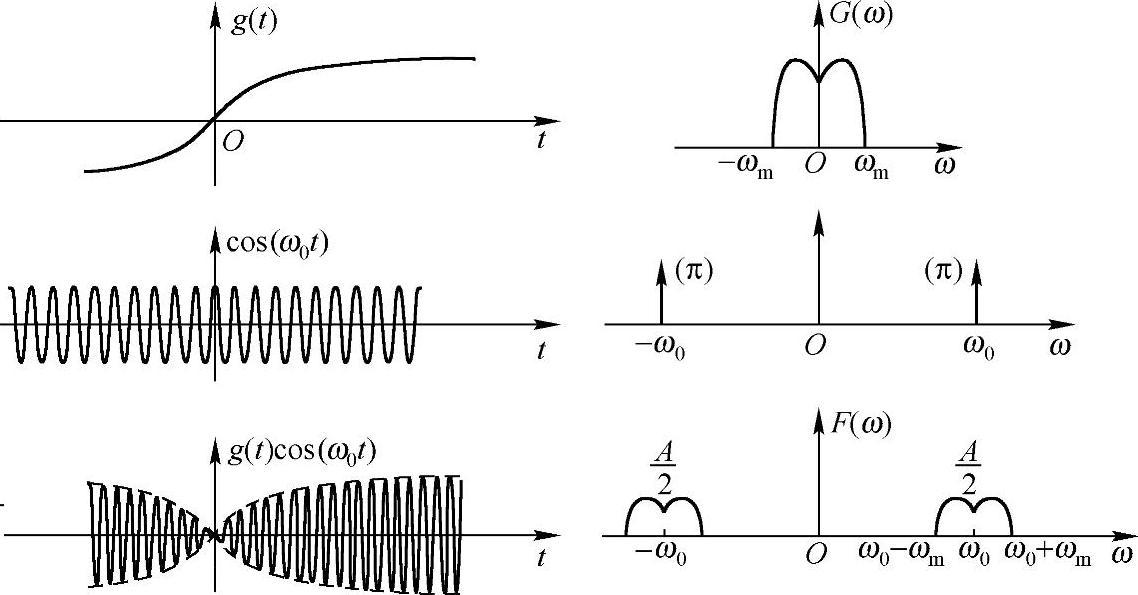
图7-8 利用余弦频谱搬移时域过程（左）和频域过程（右）

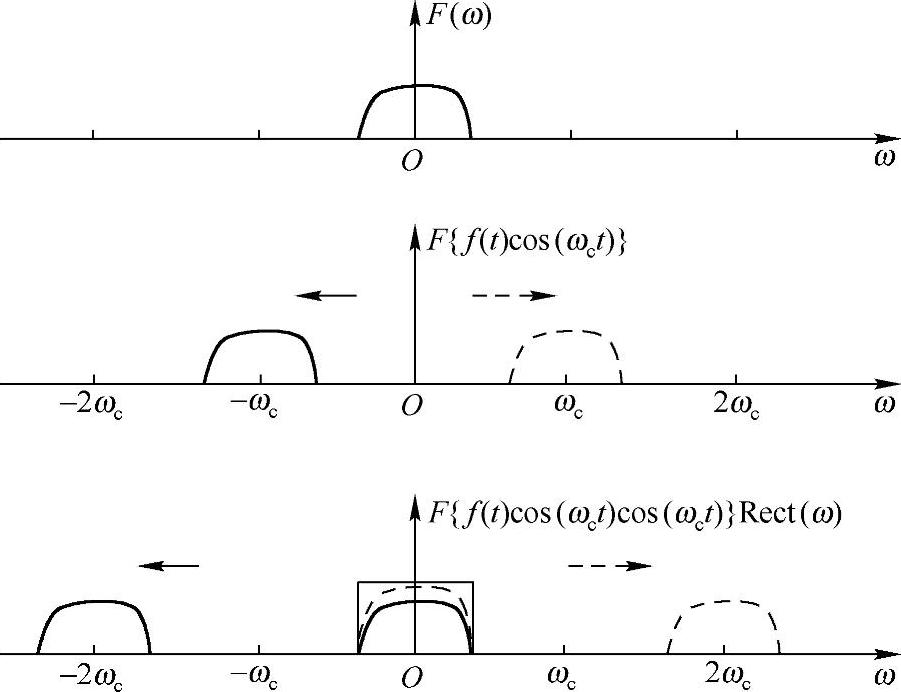
图7-9 频谱搬移以及还原(www.xing528.com)

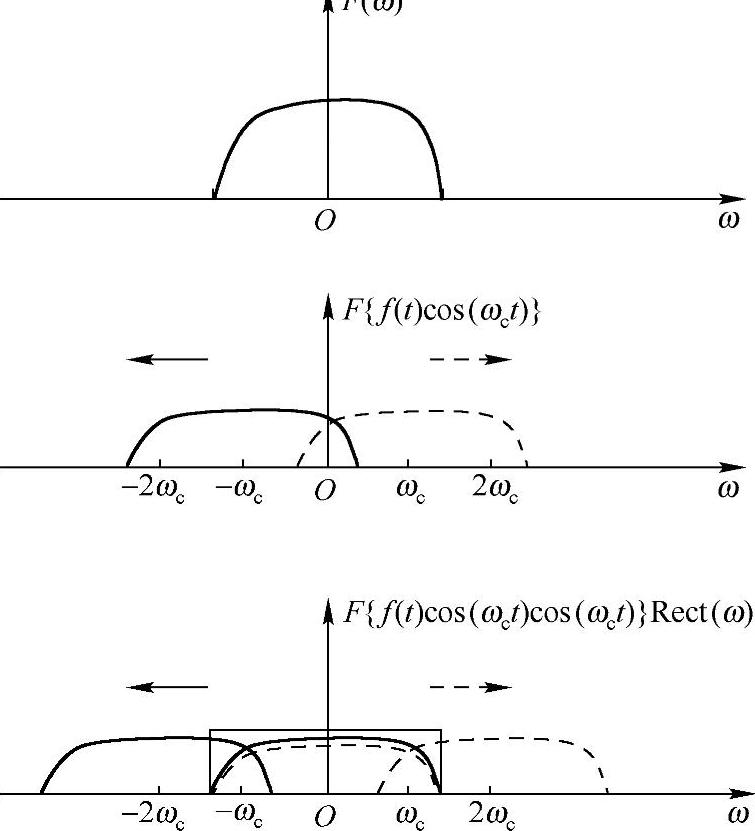
图7-10 频谱重叠导致无法滤波还原

上面我们是从正向过程来描述说明，实际上可以从相反的方向来说明。具体地，对于任何一个窄带信号s（t）（窄带信号是说信号频谱中心频点ω_c远大于信号频谱带宽），总可以找到两个信号f₁（t）和f₂（t）使得s（t）可以写成

s（t）=f₁（t）cos（ω_ct）-f₂（t）sin（ω_ct）关于这个知识点，如果要从更一般的理论上来说，就需要借助希尔伯特（Hilbert）变换以及解析信号相关的知识了，我们暂时不具体介绍，后续我们讲信号的复基带等价表示的时候，还会继续讲。

三言两语

进一步需要说明的是，因为cos（ω_ct）和sin（ω_ct）是正交的，这类似于在线性空间里的正交基下的唯一分解。区别在于正交基下的唯一分解是从代数结构去理解和考虑问题；但这里这个可以唯一还原，用到的是解析的技巧。但仅从方便理解上来说，你可以认为是正交基分解。

定义7-1（I/Q正交调制） 将两个信号f₁（t）和f₂（t）分别用余弦信号cos（ω_ct）和正弦信号sin（ω_ct）调制得到信号

s（t）=f₁（t）cos（ω_ct）-f₂（t）sin（ω_ct）的过程，被称为I/Q正交调制。其中，f₁（t）被称为I路信号，f₂（t）被称为Q路信号。

此外，这样两路同时各（调制）发送一个信号，看起来效率更高，是否真的效率更高呢？有什么理论保证？后续我们给出答案。最后，记

f（t）=f₁（t）+jf₂（t）（7-10）

注意观察知，

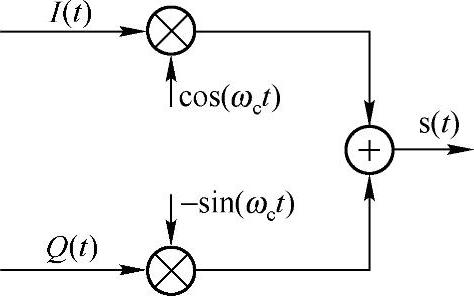
图7-11 I/Q正交调制

这个写法的用处以后再讲。