白噪声：最无序无序的声音

实际系统中，外界干扰和/或噪声总是在某种程度上存在的，不可避免的。下面我们就介绍最常见、最无章可循、又最基本的一类噪声——白噪声。

定义6-2（白噪声） 一个随机过程ξ（t）被称为白噪声，那么从频域上看，该随机过程的功率谱P（ω）在整个频域上保持不变，为一个非0常数。从时间上看，ξ（t）满足

图6-3示意了一个白噪声的一段实现。理想的白噪声从时间上看是平稳随机过程，则由其功率谱与自相关函数的关系维纳-辛钦（Wienner-Khinchin）定理知，平稳随机过程的功率谱是其自相关函数的傅里叶变换，而我们知道常数的傅里叶逆变换是冲激信号，从而知白噪声（注意是平稳随机过程）的自相关函数为原点t=0时的冲激，即对任意时刻t₁有

R_ξ（t）=E[ξ（t₁）ξ（t₁+t）]=Cδ（t）（6-8）

其中，C为和随机过程功率相关的某常数。从这个方面，我们也可以理解上面白噪声定义中时域特征和频域特征的对应关系。

由式（6-6）可以看出，随机过程时间上两个不同点所对应的随机变量是不相关的（Uncor_- related）。但一般情况下，我们把“不相关”加强成“独立”作为白噪声的时域特性（注意两个不同点所对应的随机变量独立也使得时域特征第二条成立）。再一方面，由式（6-7）可知，白噪声每个点对应的随机变量的方差为该白噪声的功率。

性质6-4（白噪声基本特性） 白噪声时间上任意两个时刻对应的随机变量独立；白噪声每个时刻对应的随机变量的方差为该白噪声的功率，即

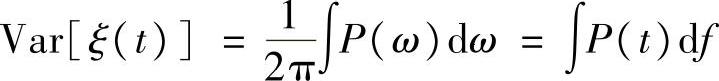(www.xing528.com)

其中，P（ω）为白噪声角频率功率谱；P（f）为白噪声线频率功率谱。

由于有这个基本特性，一般描述白噪声时，描述每个时刻所对应随机变量的方差，与描述白噪声的功率是等价的。另外，理想的白噪声功率为无穷，现实中是没有的。现实中，把有限频带内（或者说在当前考虑的系统的整个频带内）的功率谱基本平坦的噪声也当做白噪声处理。即此时也认为时间上两噪声点是独立的，每个时刻随机变量的方差等于功率。

图6-3 白噪声

定义6-3（高斯噪声） 如果一个随机过程ξ（t），对任意k>0，任意t₁，…，t_k，随机向量[ξ（t₁），…，ξ（t_k）]是联合高斯分布，则称为高斯过程或高斯噪声。

定义6-4（高斯白噪声） 既是高斯噪声，又是白噪声，则称为高斯白噪声。

值得一提的是，白噪声并不是特指高斯白噪声，它只是白噪声的一种形式，不要把概念搞混了。