高斯分布：标准而实用

常见的随机变量及分布，例如二项分布等这里也不花篇幅讲了。我们重点讲一类特别重要的随机变量及分布——高斯（Gauss）分布。

定义6-1 （高斯分布）随机变量X的概率密度函数为

随机变量X称为高斯变量，其服从的分布称为高斯分布，并记为X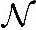～（_μ，σ²）。

图6-1给出了不同_μ，σ的高斯变量概率密度函数曲线。

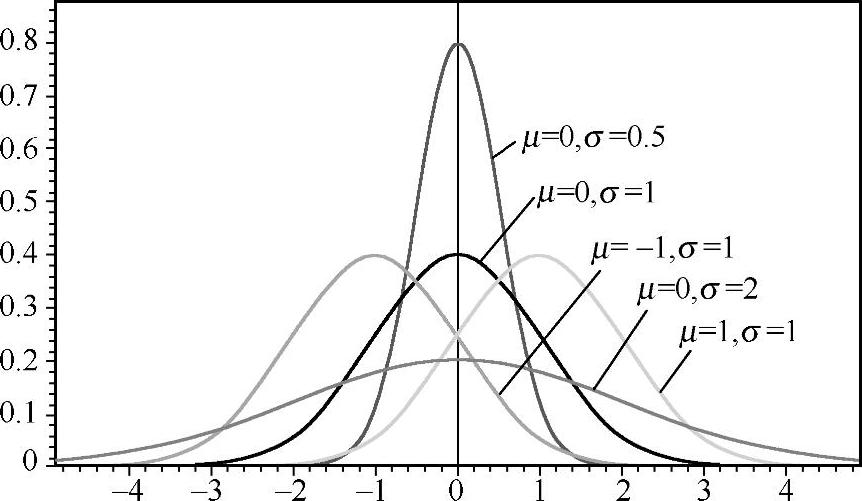
图6-1 各种高斯分布概率密度函数

显然，由概率密度函数可以确定高斯变量的累积分布函数为

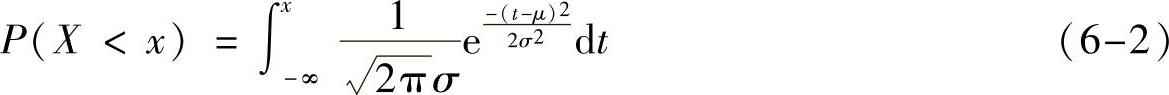
如图6-2所示。

性质6-1 （高斯变量均值和方差）概率密度函数为

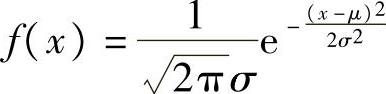(www.xing528.com)

的高斯变量X的均值为_μ，方差为σ²。

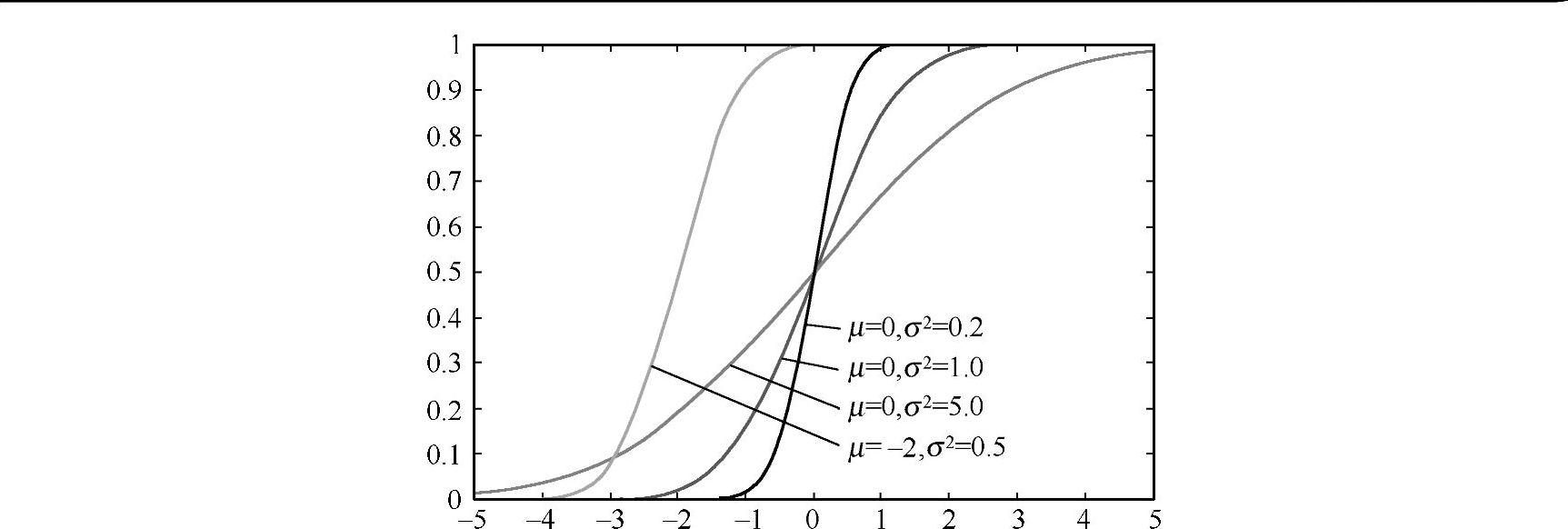
图6-2 各种高斯分布累积分布函数

三言两语

这是一个非常漂亮的性质，只要知道高斯变量的均值和方差，就能轻而易举地把完整的分布或概率密度函数写出来。

另外，从图6-1还可以看到，高斯变量的概率密度函数关于均值X=μ是对称的，并且越靠近均值的地方概率密度越大，即发生的概率越大；若均值_μ=0，则说明绝对值越小的地方概率密度越大，发生的概率越大。我们知道方差刻画了随机变量的取值相对于其均值的弥散情况，方差越小，随机变量的取值越集中在其均值周围，其概率密度函数曲线表现为越窄和高；方差越大，其概率密度函数曲线表现为越宽和扁；这从图6-1中也能看出来。下面介绍另一个很好的性质。

性质6-2（形式不变性） 几个独立高斯变量的线性组合仍然是高斯变量。假设高斯变量X₁和X₂独立，

X₁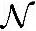～（μ₁，σ²₁），X₂～（μ₂，σ²₂）（6-3）那么，X=kX₁+lX₂也是高斯变量，且

X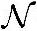～（kμ₁+lμ₂，k²σ²₁+l²σ²₂）（6-4）从形式不变性，也许我们会想，几个独立随机变量的线性组合如果是高斯变量，则是否可以说明这些随机变量也一定只能是高斯变量呢？答案是不一定。但下面只要再稍微加个条件，答案就是一定的了。

性质6-3（有限分解定理） 几个独立的随机变量之和为高斯分布，只要其中有一个是高斯分布，那么所有的随机变量只能都是高斯分布。是不是很有意思啊？有限分解定理原名是Crämer’s分解定理。