理想信道下的极限传输能力探讨

根据5.2.4节的讨论，我们说要对所有可能脉冲序列无失真，起码要求信道传递函数S（ω）和脉冲序列的取值无关，也即要求一个公共的信道传递函数S（ω）对所有可能的脉冲序列无失真。下面我们的想法可以这样，对每一个脉冲序列采样无失真的所有信道传递函数里，挑选出公共的信道传递函数，再在所有公共的信道传递函数里，挑选出频谱带宽最小的。比如，这个公共的且频谱带宽最小的其中之一有可能就是

先仔细观察得到下面一个性质：

性质5-2 对于一个脉冲序列∑_na_nδ（t-nT_s），如果按T_s等间隔采样能得到该脉冲序列的所有信号里，有一个信号的频谱带宽小于W/2=π/T_s，那么能采样得到该脉冲序列的信号唯一。如果按T_s等间隔采样能得到该脉冲序列的所有信号里，有一个信号的频谱带宽大于等于W/2=（π）/T_s，那么能采样得到该脉冲序列的所有信号里频谱带宽最小为W/2。特别地，若有一个信号的频谱带宽大于W/2=π/T_s，那么一定有多个信号可以采样得到该脉冲序列。

证明 我们先看后半部分。假设对于冲激序列∑_na_nδ（t-nT_s），能采样得到该冲激序列的其中一个信号为f₁（t），其对应频谱为F₁（ω）按间隔W的重复，其中F₁（ω）的频谱带宽大于等于W/2，不妨设等于W/2，如图5-6所示。

假设有另一个信号f₄（t）采样也能得到该冲激序列，其对应频谱带宽小于W/2，比如W＇/2，如图中F₄（ω）。那么该冲激序列的频谱应该为F₄（ω）按间隔W的重复，如图5-6所示。按理说，同一个脉冲序列的频谱应该相同，但是明显F₁（ω）的重复和F₄（ω）的重复不相等。因为对比F₁（ω）的重复，可以知道F₄（ω）的重复中间有很多“空洞”，比如图5-6中区间（W＇/2，W/2），这就造成了矛盾。所以，如果对于一个脉冲序列∑_na_nδ（t-nT_s），有一个信号的频谱带宽大于等于W/2=π/T_s，那么能采样得到该脉冲序列的所有信号里频谱带宽最小必然大于等于

图5-6 更窄信号带宽采样形成“空洞”

W/2，不可能更小。另一方面，观察知，不论序列{…，a_n，…}取值多少，信号

按T_s等间隔采样得到的采样脉冲序列为

而该信号的带宽不会大于和式（5-8）中带宽最大的分项，而分项中信号的带宽最大，也就是的带宽，即不会大于W/2。而前面刚证明了，不可能存在频谱带宽比W/2还小的信号，这意味着式（5-8）这种特殊情形的带宽只能是刚好等于W/2了。从而对于后半部分，如果对于一个脉冲序列∑_na_nδ（t-nT_s），有一个信号的频谱带宽大于等于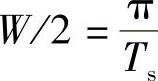，那么能采样得到该脉冲序列的所有信号里频谱带宽最小必然等于W/2，不可能更小。

按照这个思路，前半部分的证明也一样。对于一个脉冲序列∑_na_nδ（t-nT_s），如果按T_s等间隔采样能得到该脉冲序列的所有信号里，有一个信号的频谱带宽小于，那么不可能存在另一个信号按T_s等间隔采样也能得到该脉冲序列，不管其频谱带宽比W/2大还是小，因为再也找不到一个不同的频谱按W间隔重复一样，前半部分得证。

三言两语

回忆一下采样定理，性质5-2可以看成采样定理的一个对偶定理。比如，按采样定理，如果一个信号的带宽小于W/2=π/T_s，那么以T_s间隔采样得到的采样序列能唯一还原该信号。性质5-2说，对于一个脉冲序列∑_na_nδ（t-nT_s），如果按T_s等间隔采样得到的该脉冲序列的所有信号里，有一个信号的频谱带宽小于W/2=π/T_s，那么能采样得到该脉冲序列的信号唯一。同样，按采样定理，如果一个信号的带宽大于等于W/2=π/T_s，那么以T_s间隔采样得到的采样序列不一定能唯一还原该信号。特别地，如果一个信号的带宽大于W/2=π/T_s，那么以T_s间隔采样得到的采样序列一定不能唯一还原该信号。而性质5-2说，如果按T_s等间隔采样能得到该脉冲序列的所有信号里，有一个信号的频谱带宽大于等于W/2=π/T_s，那么能采样得到该脉冲序列的信号可能有多个；特别地，若有一个信号的频谱带宽大于W/2=π/T_s，那么一定有多个信号可以采样得到该脉冲序列。

根据上面的性质，我们得到如下定理：

定理5-1 对于所有脉冲序列∑_na_nδ（t-nT_s），能对所有这些序列采样无失真的信道传递函数的最小频谱带宽为W/2=π/T_s。

证明 由性质5-2，仍然分为两部分讨论。对于脉冲序列∑_na_nδ（t-nT_s），如果有一个能得到该脉冲序列的信号频谱带宽小于W/2，因为该信号是唯一的，那么过信道后采样前的信号频谱必然为该唯一信号的频谱才能保证采样后无失真。从而信道传递函数S（ω）在该唯一信号的频谱范围内需要为常数，而在[-W/2，W/2]剩下的部分可以取值任意，如图5-7所示。

而对于脉冲序列∑_na_nδ（t-nT_s），如果有一个能得到该脉冲序列的信号频谱带宽大于等于W/2，那么能采样得到该脉冲序列的所有信号里频谱带宽最小为W/2。从而要对这部分脉冲序列无失真，要求信道传递函数S（ω）的频谱带宽大于等于W/2。如果信道带宽比W/2还小，则过信道后的频谱比W/2还小，那么过信道再采样出来的冲激序列的频谱为该比W/2还小的频谱按W周期重复，无论如何也不可能是发射端冲激序列的频谱，还是因为“空洞”的原因，如图5-8所示的区间（W＇/2，W/2）。

图5-7 对于频谱带宽小于W/2的无失真信道传递函数

图5-8 更窄信道带宽采样形成“空洞”(www.xing528.com)

从对这两部分脉冲序列的无失真讨论来看，能对这两部分同时采样无失真，频谱带宽最窄必然为W/2。特别地，该无失真信道传递函数S（ω）可以为[-W/2，W/2]上的方波，即时域冲激响应为sinc（πt/T_s）。

通过前面的讨论知，在有效传输的情况下，无误传输的信道带宽最小为W/2。而单位时间内传递的符号个数是一样的，带宽越小，频谱效率越高，效率最高为单位时间（秒，s）单位带宽（赫兹，Hz）可传输的数据符号数为

即2个数据符号每秒每赫兹（2 Symb/s/Hz）。

定理5-2 （采样无失真最高频谱利用率）给定系统带宽，在采样无失真的情况下，频谱最高利用率为单位时间（秒，s）单位带宽（赫兹，Hz）传输2个数据符号，即2Symb/s/Hz。这个速率也被称为奈奎斯特传输率。

由上面的讨论，采样点无失真的（广义）信道传递函数此时可以为

现在要传输这个数字序列，发射端可以选用的基本信号为

此时狭义信道传递函数为

那么，这个系统接收端理想采样出来的就是发射端数字序列。

前面讲的是狭义无失真，现在我们考虑广义无失真的情况。例如，过信道在接收端采样得到的不是∑_na_nδ（t-nT_s），而是

看起来，采样点失真了，但是注意到只要a_n-1和a_n-1+a_n正确接收了，a_n显然也能正确接收，依次类推，就没问题了。这个采样序列可以看成

观察知，接收端采样后能得到这样一个采样序列，信道响应可以是

则该系统广义下也是采样点无失真的。并且信道的带宽（信道响应的带宽）相对于狭义无失真最高利用率情形没有增加，所以该系统也能达到最高频谱利用率2symb/s/Hz。该系统信道响应如图5-9所示。

图5-9 部分响应系统的信道响应

当然，该系统只要前面一个a_n-1错了，后面的基本上都错了，即错误扩散。不过可以通过先对要发送的序列{…，a_n，…}进行预编码再发送的方法来消除错误扩散。这部分内容在一般通信原理教材上就是部分响应系统的内容，更细节的讨论本书就不讲了，请大家自行查阅资料了解。