简化信号接收和DFT处理

现在有个现实问题需要解决：在上面的讨论中，接收端要获得发射端的数据，需要计算不同基下的坐标N次，而每个坐标的计算都要用积分运算，即要用N个积分器同时工作才能分离数据符号。当子载波数量相当多时，每个子载波都需要一个相应的积分器，这样实现成本太高，系统太复杂。这一问题如何解决呢？先看一下下面给出的公式。

记一个OFDM符号长度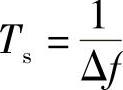f。对接收信号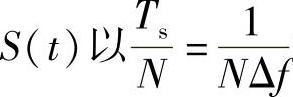为间隔采样，得到N个采样点A_n（n=0，…，N-1），则有

可以发现，采样点和序列a_n的IDFT的值相等，这样在接收端先对信号S（t）采样再进行DFT就可以还原a_n了。无论是采样还是进行DFT/IDFT运算，随着数字信号处理（Digital Signal Processing，DSP）能力的提高，相对于积分器来说，都变得简单了很多，这也使得OFDM技术更快地被纳入实际系统应用中。

并且，在接收端来说，采样N个点理论上是足够精确的。当然，也可以以任意大于N的整数来采样N_c>N个点，此时采样点序列为

其中，当k>N时，a_k=0。要得到真正发出的那些a_k，0≤k≤N-1，取A_n的DFT的前N项就可以了。实际系统中，一般为了用得上快速算法FFT/IFFT，一般取N_c>N且为2、3、5的幂次，即N_c=2^a3^b5^c。(www.xing528.com)

三言两语

最后必须强调，不管发射端采取什么操作，只要保证最后发出的信号确实是S（t），那么接收端通过采样操作再进行DFT运算，理论上是一定能无误地得到发射端各子载波承载的数据的。换句话说，接收端的行为和发射端无关，特别地，和发射端是否采用IDFT没有任何关系。

思考一下 这里的采样点如果不是用来做DFT变换以求出a_n，而是用来先插值还原原信号波形，再按基本原理的积分器能无误还原出a_n吗？