全面解析离散傅里叶变换（DFT/IDFT）：实现完美的数据转换

注意到，由式（4-34）、式（4-36）定义的离散时间序列的傅里叶变换仍然是以2π为周期的连续信号（先不看自变量的限制范围），只要知道任何一个周期的频谱，就可以还原任何自变量范围的频谱，但还不是离散的。为了和其他资料保持一致，接下来我们把自变量范围稍微调整一下，调整到[0，2π]。要离散化，我们知道最简单的操作就是“采样”。那我们就在[0，2π]区间上等间隔采N_c个点看看有什么发现。这N_c个点为

再提醒一下，我们的初衷当然不是为了形式上的离散化而离散化，而是在还原意义上的离散化，即通过离散化出来的值我们能通过某种手段（或规则）知道这些离散值对应哪个离散序列的傅里叶变换连续谱。这里就是，通过N_c个点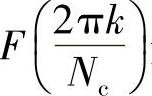知道N个点的离散序列f_k。也就是说，它们需要有个一一对应的关系。那它们有一一对应的关系吗？通过对三种情形讨论：N_c<N，N_c=N，N_c>N，知，后两种情形可以使得有一一对应关系，具体讨论见附录C。由此，我们可以总结得到离散傅里叶变换及逆变换（DFT及IDFT）相关知识。

定义4-2（离散傅里叶变换及逆变换）两个长度为N的序列x_n和X_n可以通过一对互逆运算相互一一确定

通常，仍然称x_n为时域序列，X_n为频域序列。当然，序列x_n与X_n的关系也可以用如下的矩阵形式表示出来：

式（4-40）右边那个大矩阵一般称为DFT矩阵（本书记为[DFT]），其逆矩阵也就是IDFT矩阵（本书记为[IDFT]）。

下面简单说明一下IDFT。注意到式（4-40）等价于

也就是说，DFT之后序列X_n是N个向量的线性组合，而这N个向量我们已经证明过是正交的（见附录C），也就是一组正交基；另一方面，DFT之前序列x_n可以看成分别是这些基下的坐标，从而要给出IDFT的公式，其实就是计算序列X_n在各个基下的坐标。回忆一下普通向量的内积定义形式以及正交基下坐标计算公式可知，序列X_n在第i个基(www.xing528.com)

下坐标为

当然，同样，如果先有IDFT的定义，则DFT公式等价于求序列x_n在另一组基（取个共轭）下的坐标。

如何快速计算一个序列的DFT或IDFT呢？对应的快速算法有快速傅里叶变换及逆变换（FFT及IFFT），本书不详细讲了，请读者自行查阅相关文献。

三言两语

最后再强调一遍，离散傅里叶变换是用离散数据来分析信号频谱的工具，一定要把如何从信号的连续谱过渡到离散数据的离散傅里叶变换的原理搞清楚，不然凭什么说它可以用来分析频谱，凭什么把两个序列一个叫时域序列，一个叫频域序列，它们就是两串能等价表示的数而已！