实现信号的采样与重建方法优化

1.现实之信号时域有限

现实中，信号都是时域有限的，就是说频带是无限的，就不可能完全无误地恢复信号了，怎么办？

回到采样后的序列频谱推导，可以看到不管被采样信号频谱是否有限，采样后的频谱为被采信号的频谱的周期重复。只不过，当频谱无限时，无论怎么采样，重复的频谱片段都是有交叠的。然而，当我们以能量集中的那部分频谱（比如包含99%能量）带宽为准，进行采样后，可以使得至少能量集中的那部分不会相互重叠。从而加个滤波器可以把能量集中的那部分滤出来，得到信号的近似频谱，当然也得到原信号的近似信号。现在，我们会发现滤出来的那部分相对于被采信号真实的频谱来说有两部分误差：其一是被截断了（如图4-8中斜线阴影部分）；其二是，即使是保留的那部分也不是和简单截断能量集中之外剩下的部分，原因是其他重复片段也有一小部分延伸进入被滤出的那一部分了（如图4-8中格子阴影部分）。这两部分引起的误差，可以认为在时域叠加了干扰。若引起误差部分能量很小（比如1%），根据能量守恒，也就是在时域所叠加干扰的能量很小。在允许的失真范围内，采样定理还是有现实指导意义的。

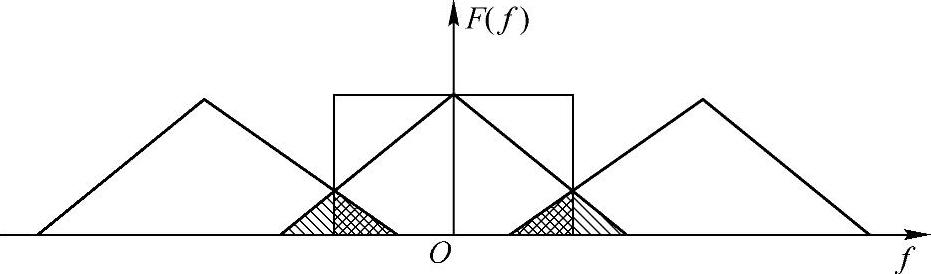
图4-8 不同阴影部分所示两部分误差

2.现实之非理想冲激采样

上面讲了现实中不可能有真正满足奈奎斯特率采样的信号。采样信号也一样，前面理论讨论中，采样信号为理想的周期冲激信号序列，现实中也不可能真正实现的。现实中，采样电路不可能采样一个点后，瞬时就断掉了，总是需要持续一定的时间。比如零阶保持采样，每采样一个点，产生一个以采样点为幅度的方波信号，如图4-9所示。

不过大家一定不要把零阶保持采样和信号乘以周期方波信号混淆了，后者的效果如图4-10所示，注意区别。

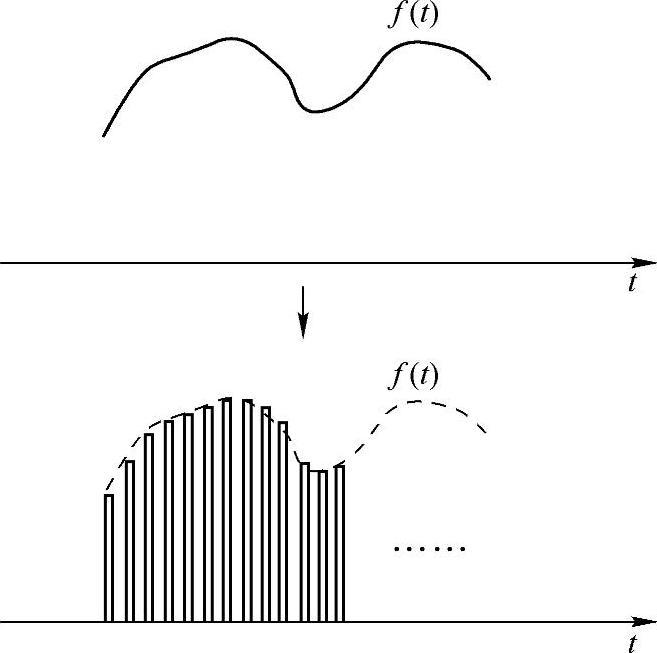
图4-9 零阶保持采样信号

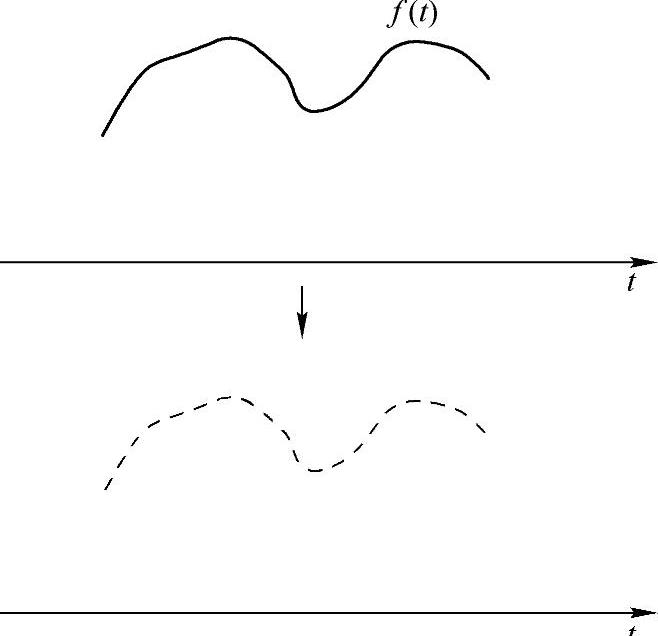
图4-10 信号乘以周期方波信号

零阶保持采样后的信号形如

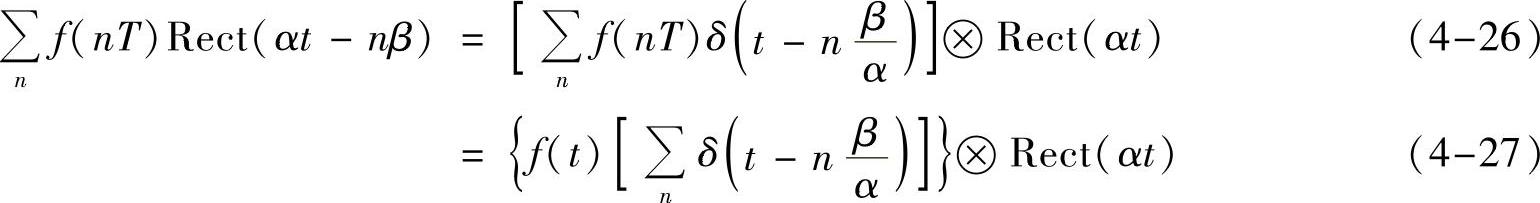
而信号乘以周期方波信号得到的信号形如

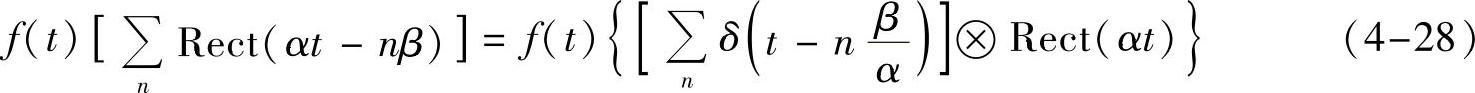
前者为先乘积再卷积，后者为先卷积再乘积，其中α，β的值可根据具体情况来定。整个零阶保持采样的时域变换等价过程为：先对信号f（t）用冲激信号采样得到采样冲激信号序列，该冲激信号序列再和一个方波信号卷积。该等价过程的时域变换和频域变换如图4-11所示。

假设信号f（t）的非零频谱区间为[-W，W]，对于零阶采样后的信号，若要理想还原，只需要加一个频谱如下的滤波器就可以了：

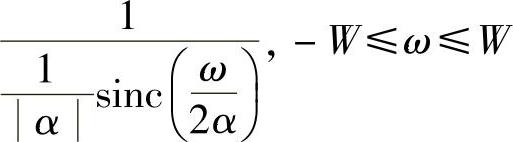
这个过程也可以分解成两个步骤来看，先加了一个如下所示的频谱无限的滤波器：

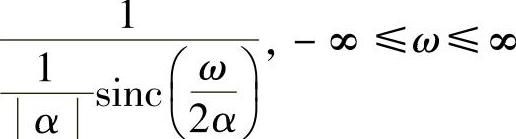
接着又套了一个理想矩形滤波器其他形状的非理想冲激采样信号的分析与此类似，不一一讨论了。

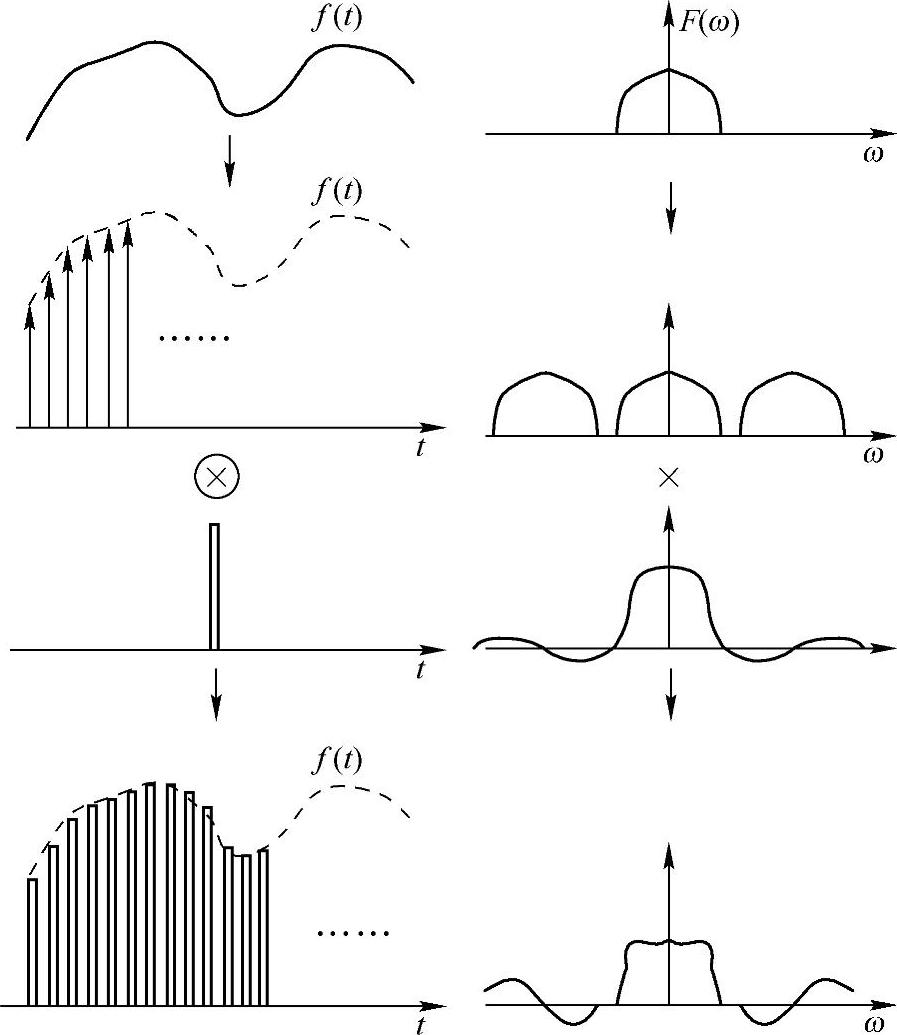
图4-11 零阶保持采样等价时域（左）和频域（右）过程

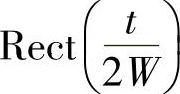
3.现实之非理想滤波器(https://www.xing528.com)

前面采样后讨论的频域滤波器都是理想的，即可以刚好滤出想要的那一段，其他部分为0。这样一个滤波器现实中本来就是没有的，因为该滤波器作为一个系统的传递函数为频域有限的，其时域冲激响应必然是无限的，这样的滤波器不可能现实存在。现实中的滤波器必然时域冲激响应是有限的，从而频域必是无限的，从而采样后滤波时也不是刚好只把一段给滤出来了，其他段也会有。好在，虽然我们不能把滤波器频域做成有限的，但是可以把想要的频带之外的部分其取值尽量做小，比如频域信号sinc（αω）虽无穷，但尾巴是衰减的。这样其他段虽有，但是可以保持能量很小，从而和上面类似，等价于时域叠加了个小干扰，也许还可用。当然，sinc（αω）的尾巴衰减还不够快，可以做到衰减得更快，尾巴更小，比如下面定义的采用升余弦滚降滤波。

定义4-1（升余弦滤波器）升余弦滤波器（Raised-cosine-filter）的频域（线频率）定义为

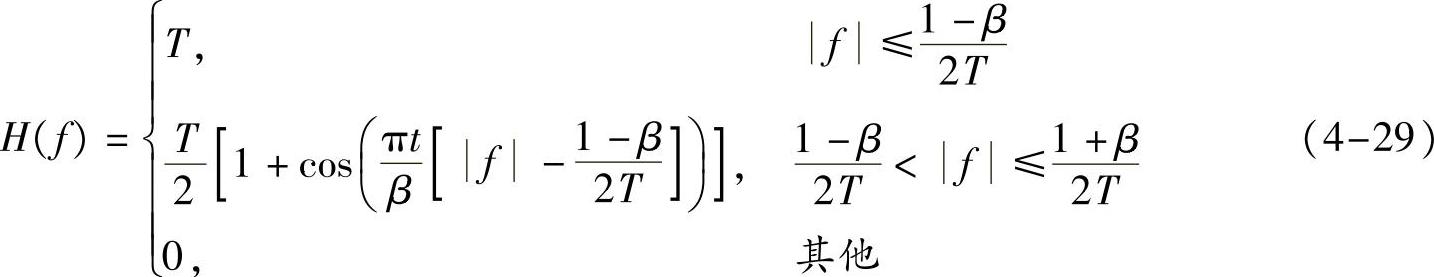
其对应的时域信号为

其中，β称为滚降系数。

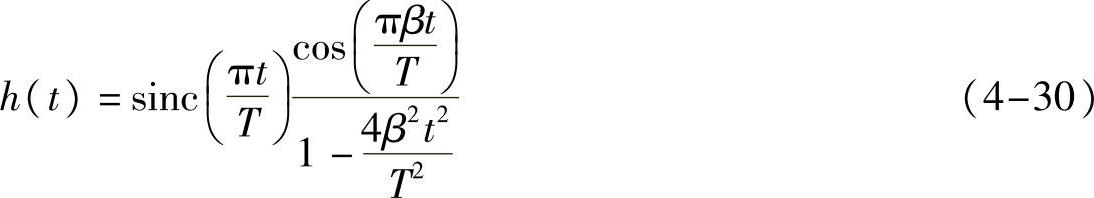
图4-12和图4-13示意了不同滚降系数的升余弦时/频域信号。从中可以看到，理想滤波器（或sinc信号）其实是对应于滚降系数为0的升余弦信号；而尾巴最小的是滚降系数为β=1的信号。

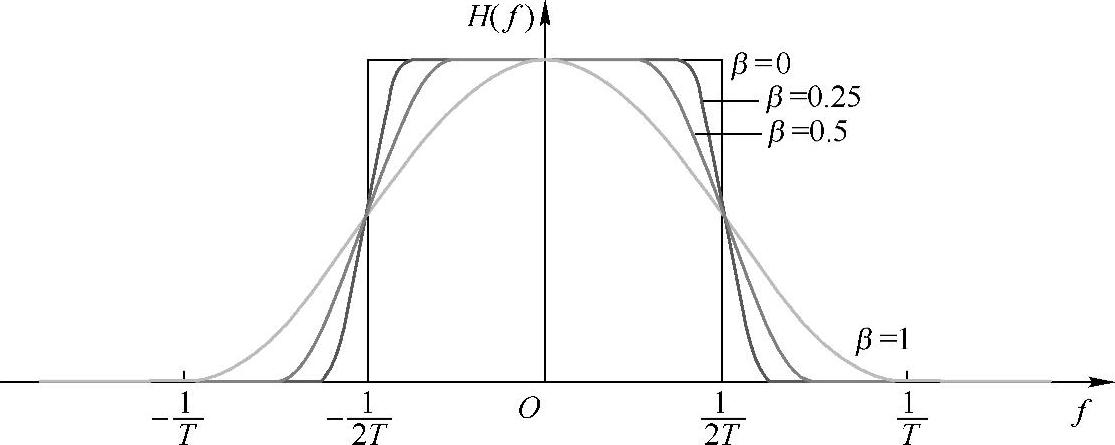
图4-12 不同滚降系数的升余弦频域信号

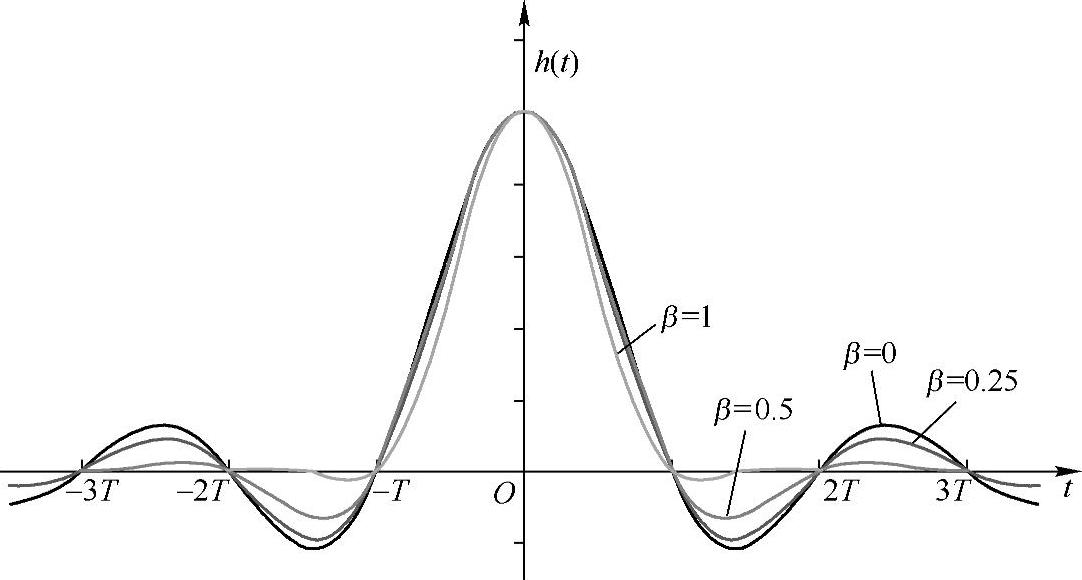
图4-13 不同滚降系数的升余弦时域信号

4.略做小结

通过上面的讨论，我们知道现实采样面临如下这些问题：

●不可能满足奈奎斯特率。

●不可能冲激采样。

●不可能理想滤波。

后续我们不会具体讲解现实中如何采样，有哪些现实滤波器等，这些内容请大家以前面讲的理论为基础去学习更专业的课程或专业资料。下面，我们只提前给大家一些定性的概念。

现实中采样没有一样和理论采样条件相符合，并不代表采样理论完全没用，因为我们需要分析评估所设计的现实采样系统的性能，还需要借助采样理论分析，至少作为分析中间过程不可或缺的一步。比如，上面讨论的零阶保持采样，我们分析时，采用的等价过程中就借助理想情况作为中间过程来分析。所以，理论仍然是最基本的，需要深刻理解。

虽然有这么多非理想因素，现实中以能量集中部分带宽为基础的现实采样，再现实滤波还原出来得到的信号，从时域和频域来看，都可以足够近似原信号。

另一方面，在后面将要重点讲到的数字通信，大多数时候，更不要求电磁信号完全精确，足够近似就可以了。当然，这也是数字通信的一个优点。

最后，前面所有关于采样的讨论都是以基带信号为基础的。但信号不一定都是基带信号，如果信号是频带信号会怎么样呢？回忆频带信号一般指频谱非0范围不是刚好在零频（ω=0）附近的那些信号，比如频谱非零范围为0<W₁≤ω≤W₂或者频谱非零范围为[-W₂，-W₁]∪[W₁，W₂]等。关于频带信号采样，本书不打算详细讲，分析方法和上面类似。毫无疑问，频带信号可以当成一种特殊的基带信号来处理，即仍然以大于最高频率两倍来采样，一定可以无失真还原。比如，即使频带信号为cos（ω_ct），我们也可以以大于2ω_c速率采样来还原。但问题是，频带信号的最高频率可能很高，这样的话采样速率要求太高了。同时，人们又注意到，虽然最高频率很高，但真实非零带宽可能很小，有没有可能将采样速率与真实非零带宽联系起来呢？从而以更低的采样速率达到无失真效果。这也是频带信号采样主要研究的内容。

答案当然是有可能的，具体是多少，留做练习，请读者朋友自己推导。原理和基带信号常规推导方法一样，反正以任何速率采样，都是信号频谱的重复，只要弄出一份没有重叠的频谱就好了。

小结（采样定理的现实意义）对于现实通信系统来说，要发送和接收的信号的宽度是根据提前设计的通信系统占用的频带宽度来设计的，是受限于系统频带宽度的。比如，通信系统将要运行的频率及带宽为1920～1925 MHz，那么所有在这个通信系统里发送接收的模拟信号带宽不能超过5 MHz，至少能量集中部分不能超过5 MHz。并且，发射端设备和接收端设备的制造设计者当然也是提前知道这一点的。对于发射端设备来说，它要发送这么宽的信号，首先它得生成这么宽的一个信号。怎么生成简单呢？要知道带宽不超过5 MHz的信号有无穷多，这些模拟信号可是千差万别的，如果每个信号都直接由电路实现，那电路会非常复杂。这时，要是在生成这些模拟信号的每一个模拟信号之前，先通过其他办法（这里先不讲哪些具体办法）知道当前要生成的模拟信号的满足采样定理（现实意义下满足）的采样序列那就好办了：我的电路只需要实现一个波形的模拟信号，即sinc信号，就可以了。其他所有模拟信号都可以利用sinc信号和采样序列、做一些简单的机械的放大/缩小、平移/相加就都可以实现了。

另一方面的现实意义是，目前的趋势来说，数字手段的通信的应用越来越多，而数字手段首先要涉及数字化，或者说离散化，而显然采样就是很简单直接的一种对模拟信号的离散化手段了。先说这么多，后面我们还会具体讲。

再来和泰勒（Taylor）展开比较，采样定理和泰勒展开有什么区别啊？从表示论来说，没什么区别，两者都是通过一序列离散值来决定原连续信号。用线性空间的观点来看，就是同一向量在不同基下的表示，坐标不同而已。话虽如此，但还是有一些细节区别的，比如通过泰勒展开，很难看清楚信号到底会有什么样的具体取值；而通过采样定理，至少知道采样点的位置的取值；另一方面，从实现来说，采样定理重建原信号只需要把同一个信号简单地乘以一个系数，平移、相加就行了，都是简单的操作，而泰勒展开就复杂得多了，泰勒展开处理的基本单元是不同阶数的指数函数xⁿ。