4.1.3拿信号的DNA克隆原信号

假设现在已经使得相邻两个重复片段没有交叠，即ωp>2Wc。要重新得到f(t)，只需要让采样后的信号通过一个滤波器滤出一片频谱即可，我们就滤出频谱原点（零频）附近那一片吧，如图4-3所示。该所谓滤波器其实为一个线性系统，其传递函数为

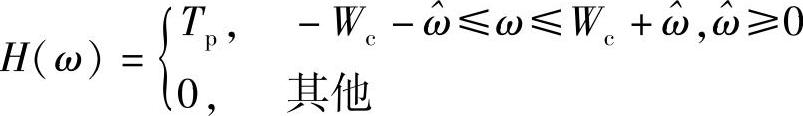
则，容易看到

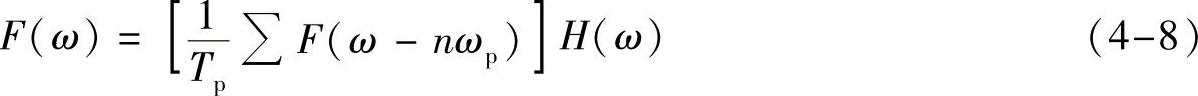
只要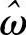在两个重复频谱片段的间隔之内，即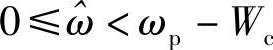，式(4-8)就是恒成立的。

当时，即滤波窗宽度刚好等于信号的非零频谱宽度，下面讨论中称为截止频率滤波，如图4-4a所示：当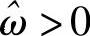时，也即我们在滤波时，不是刚好只把一份频谱滤出来，而是多滤了一些（空白部分）出来，下面讨论中称为非截止频率滤波，如图4-4b所示。

注意到，上面式(4-8)中我们已经在频域还原了信号f(t)，即得到了F(ω)。但从得到的结果似乎不能比较直观地看到采样的痕迹，那就没意义了，不过也许在时域信号表示上可以看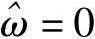到。那下面我们就把F(ω)通过傅里叶逆变换变到时域看看。

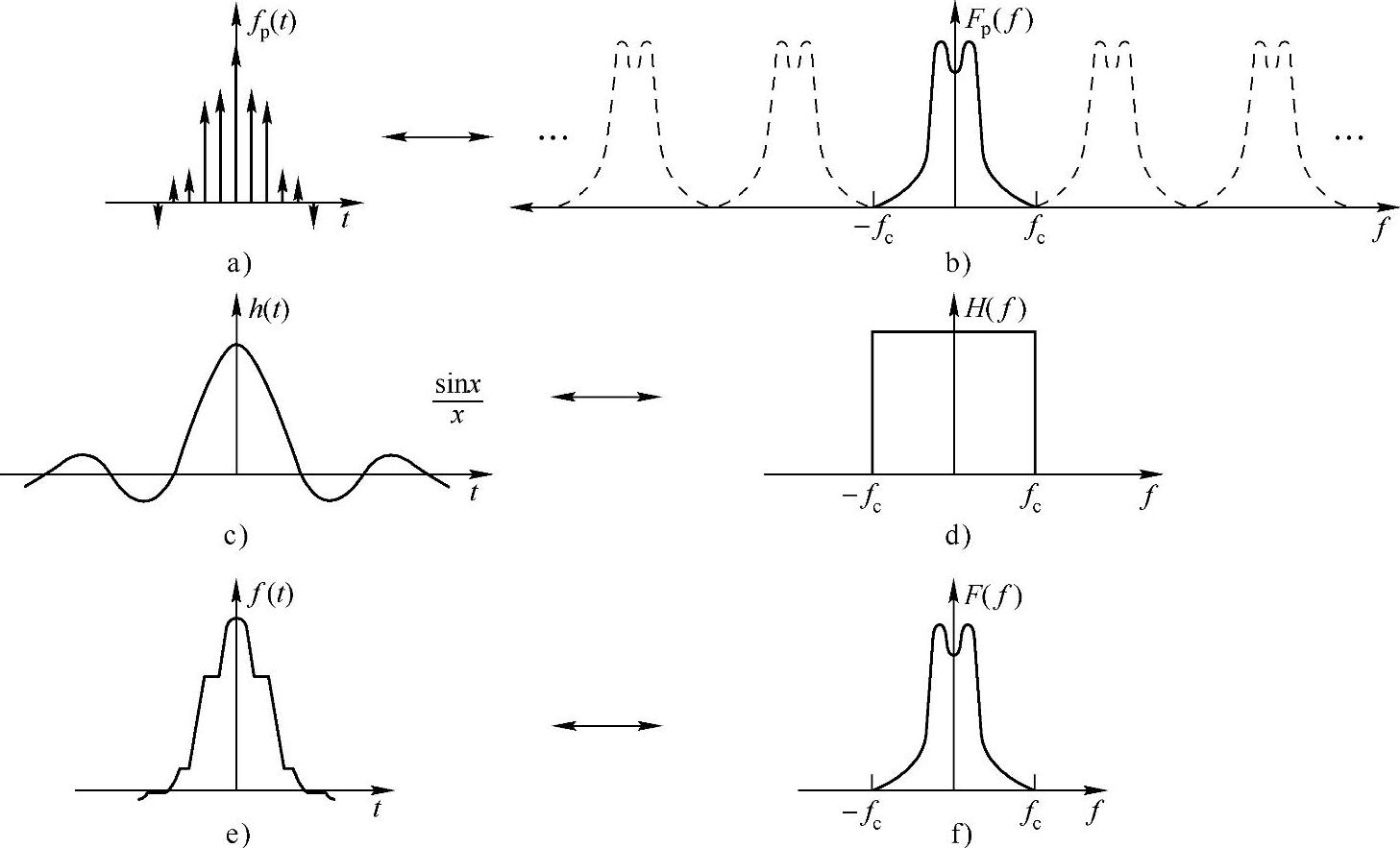
图4-3 信号还原时域过程（左）和频域过程（右）

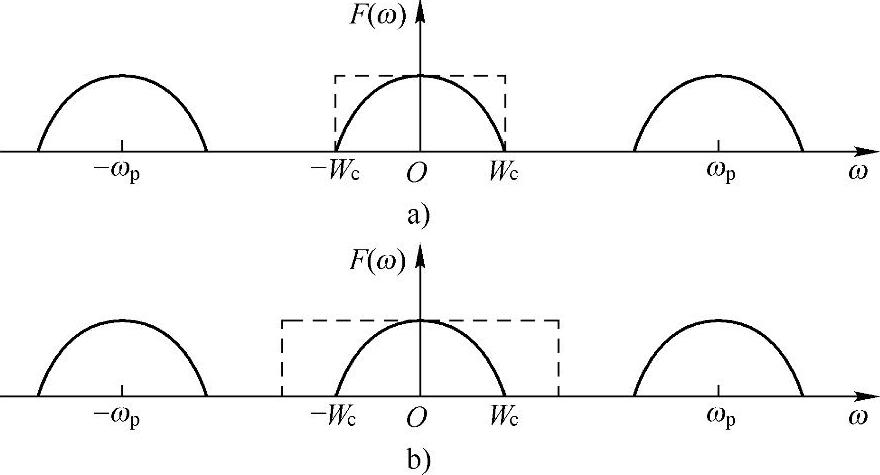
图4-4 截止频率滤波和非截止频率滤波

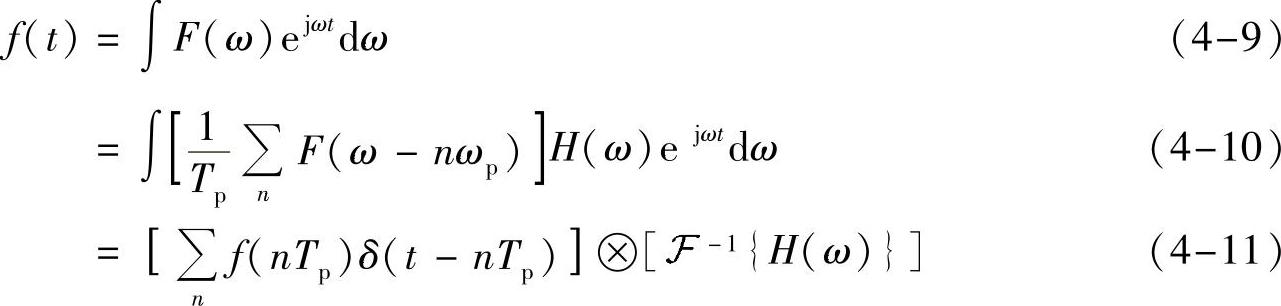
上面最后一步用到傅里叶变换“频域乘积，时域卷积”性质。注意到，

那么，南讲过的方波信号傅里叶变换，可得

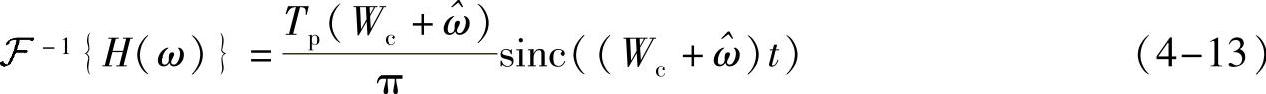
代入式（4-11）继续展开．得

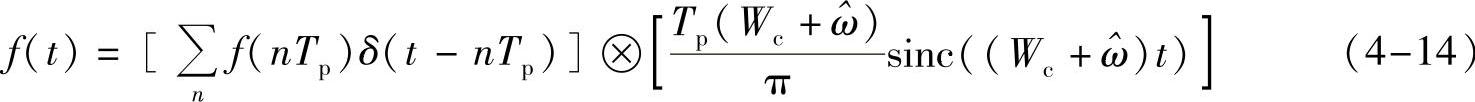
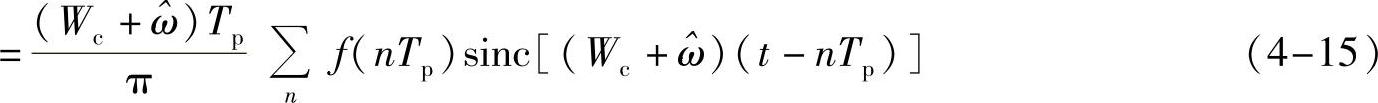
可以看到在满足采样定理的前提下，信号f(t)可以由采样点按照式（4-15）重建，或称为用采样点进行插值，用到的插值信号为slnc信号，如图4-5所示。

从上面的讨论中，我们知道在满足采样定理的前提下，信号总是可以写成采样点与某个slnc信号相应平移的线性叠加，并且还比较灵活，形式多样：(www.xing528.com)

1)首先，采样点的距离在大于奈奎斯特率前提下可随意调整；

2)即使把采样点距离同定，每个采样点处对应的slnc信号（宽度）也是可变的，由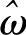决定。

下面我们再举一些例子来体会一下。

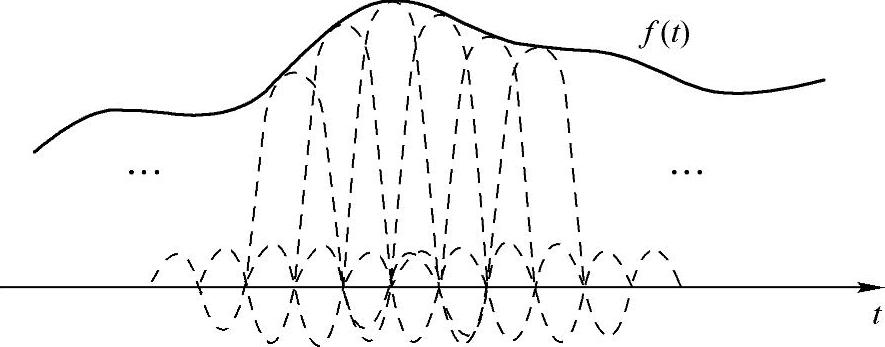
图4-5 信号由sine信号重建

例4-1 仍然假设信号f（f）的非0频谱范围为[-W，W]。假设采样速率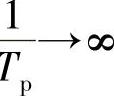，即采样间隔TP—0。此时，两段重复片段相隔无穷远。但我们加窗滤波还原时，仍按截止频率加窗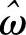（=0)。由式子(4-15)可以看到，最后还原的信号被表示为

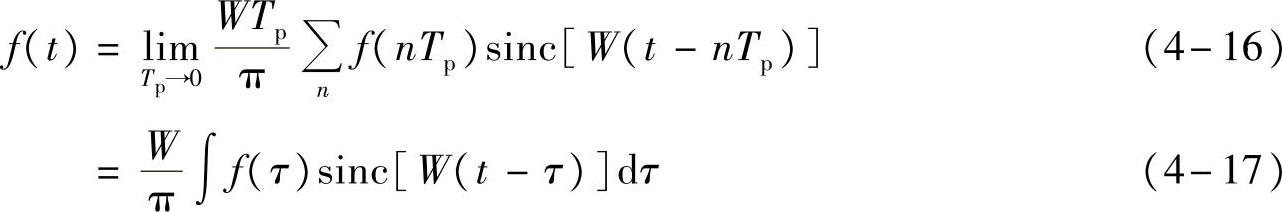
这说明，信号f(t)可以表示成．f(t)与smc信号的卷积。

其实，这很显然，因为任何信号f(t)的频谱F(ω)总是可以写成

F(ω)=F(ω)Rect(αω) (4-18)

其中，“与信号f(t)频谱宽度相关。根据“频域乘积，时域卷积”性质可知，必然信号．f(t)可以表示成f(t)与slnc信号的卷积。

例4-2 仍然假设信号f（t）的非0频谱范围为[-W，W]。假设采样速率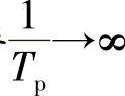，即采样间隔TP→0。此时，两段重复片段相隔无穷远。但我们加窗滤波还原时，加一个无穷大的窗，即

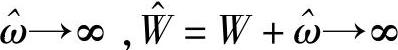
由式（4-15）可以看到，最后还原的信号被表示为

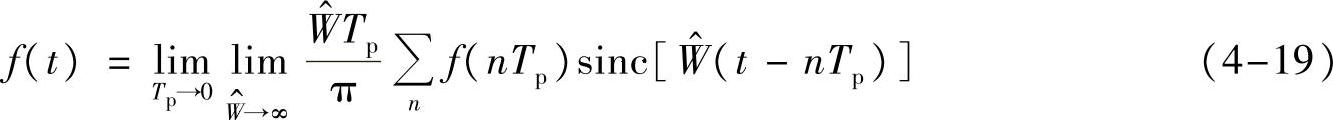
由如何从sinc信号产生冲激信号的讨论（见附录C）知，

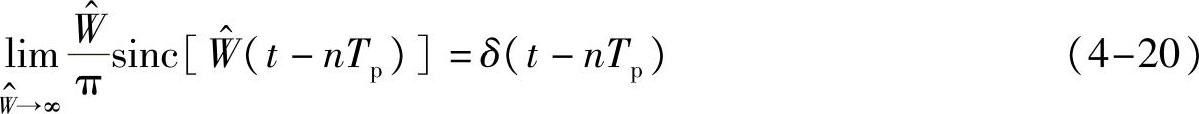
则

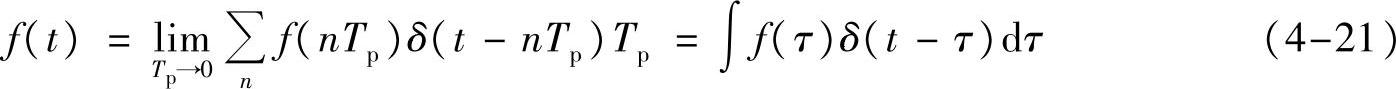
怎么样，是否很熟悉？这不就是任何信号的冲激分解嘛！