周期信号的傅里叶变换

周期信号有傅里叶级数，那周期信号有傅里叶变换吗？大家回顾一下，我们在推导傅里叶变换时，并没有限定区间τ≤t≤τ+T0，T0→∞上的信号一定不是周期函数，那就是说，傅里叶变换也可以推广到周期函数。下面我们就简单看看周期信号的傅里叶变换是什么样的。

性质2-10（周期函数的傅里叶变换） 设f(t)是以T1为周期的函数，则f(t)的傅里叶变换

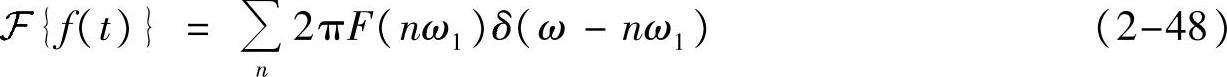
其中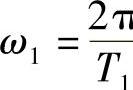，，且

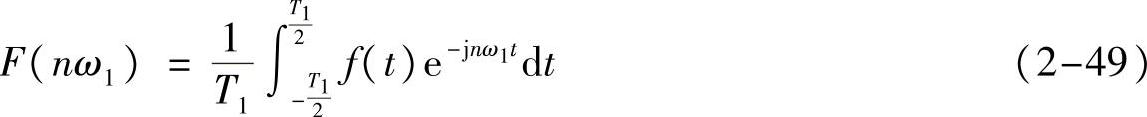
证明 假设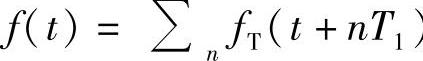其中f(t)为一个周期内的函数。可以利用周期函数的傅里叶级数表示和傅里叶变换的线性性质简单推导如下：

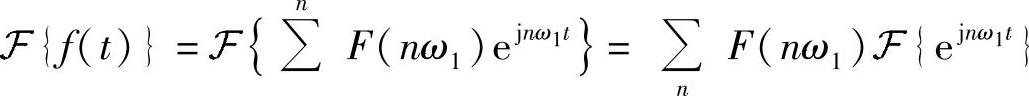
再结合傅里叶变换“复指数函数的傅里叶变换”性质，我们得到周期信号的傅里叶变换

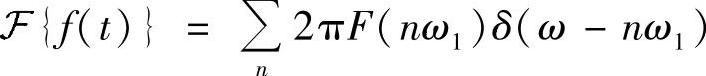
其实由傅里叶变换的实质来理解这个也很直接，我们再说一遍，傅里叶变换的实质是求坐标。而根据周期信号f(t)的傅里叶级数表示

(www.xing528.com)

我们知道，周期信号在各个基下的坐标已经在那儿了，我们只需要按傅里叶变换的定义把傅里叶变换提出来就行了。注意，信号在某个基下的坐标是其傅里叶变换乘以公共量。那么，因为在基下的坐标为F(nω1)，从而从傅里叶变换来说，该频点对应的傅里叶变换为

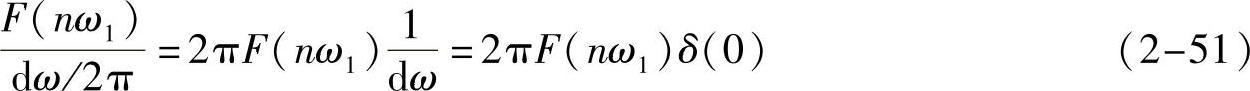
注意到，只有在频点ω=nω．才有这个冲激值，在其他频点为0，仍然和冲激信号定义对比，可知周期信号的傅里叶变换为一系列冲激。

另外，注意到各冲激的幅度

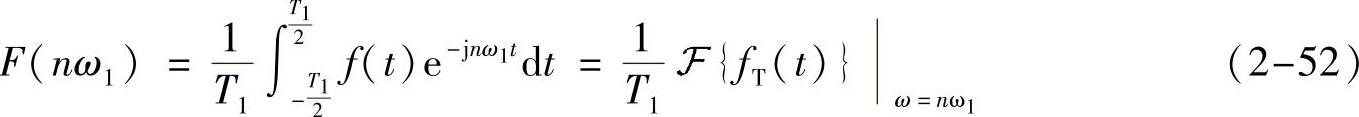
这说明周期函数的（傅里叶变换意义下）频谱是其一个周期所示函数的频谱的等间隔冲激抽样。

例2-2（周期方波的傅里叶变换） 周期方波以及其对应的傅里叶变换如图2-9所示，大家感性认识一下，注意和非周期方波信号及其傅里叶变换slnc信号对比看是否是某种采样的关系。

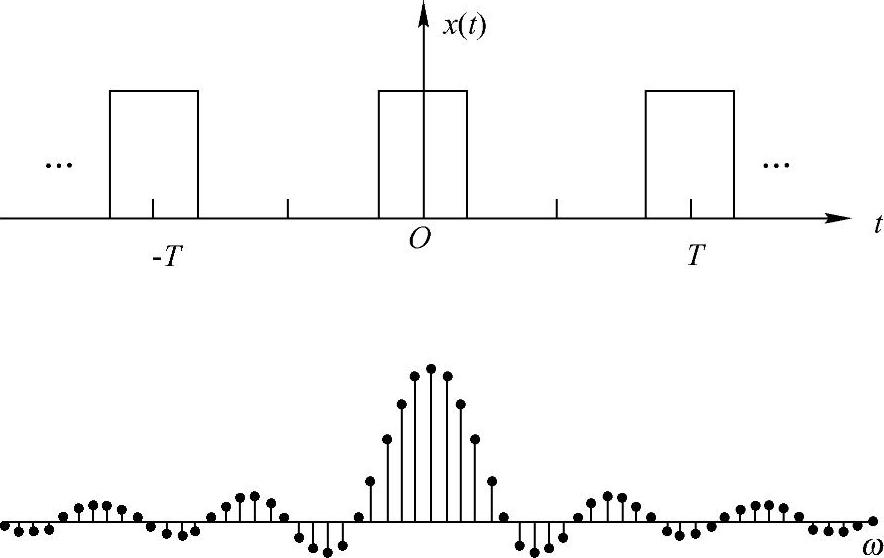
图2-9 周期方波信号与其傅里叶变换