探究信号频谱：你是否有男高音潜力？

很多情况下，我们通过听声音就可以知道是谁在说话，比如周星驰电影的配音，这是为什么呢？是凶为他说话声音大？绝对不是。而是因为其声音在各频率分量上的强弱与其他人不同。图2-8里给出了一段声音信号在时域和频域的对比，从中可以看到我们人类的声音，在频率上看，仅落在0-4000赫兹(Hz)区间里。一个人的声音从频率上看，如果长得和大多数人很不一样，那么这个人的声音辨识度就很高。

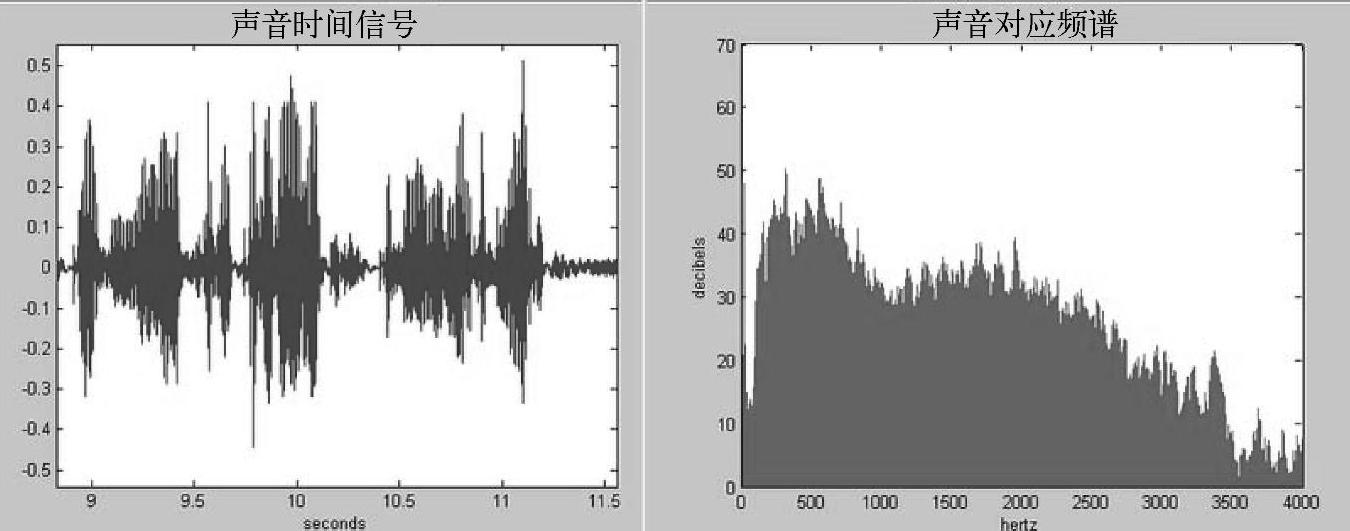
图2-8 人的声音频谱

类似地，这就是为什么在实际问题分析中，我们希望看到一个信号在各个频点上的能量分布情况，即坐标的模的大小分布情况，为此定义了下面能量谱密度和功率谱密度的概念。

定义2-2（能量谱密度） 对于能量存在且有限的信号f(t)，称

S(ω)=∣F(ω)∣2 (2-40)

为它的能量谱密度。显然，如字面意思，既然是密度．总能量就是整个区域的累积．如果采用线频率就没有前面系数：

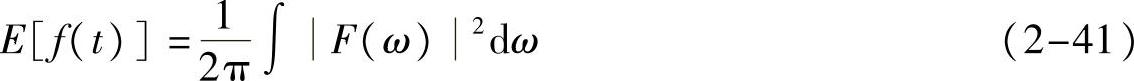
定义2-3（功率谱密度）对于功率存在且有限的信号，上面的能量谱密度的积分为无穷大，所以不方便以总能量来刻画，而是用单位时间内的平均能量，即功率来刻画。单位时间内的功率为

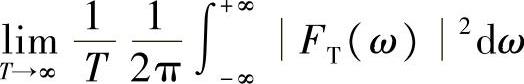
其中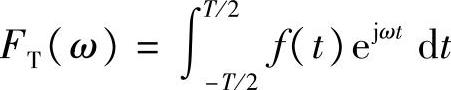，，即信号f（t）的截断的傅里叶变换。对比能量谱密度与总能量的关系，我们把

称为功率谱密度。

同样如果认为系数1／（2π）碍事，可以采用线频率傅里叶变换表示。

类似于随机信号的能量与功率描述，对于随机过程ζ(t)来说，能量谱密度和功率谱密度也需要从统计上来看。

●能量谱密度 对所有ζ(t)的可能实现f(t)的功率谱密度S(ω)取统计平均

S(ω)=E{∣FT(ω)∣2} (2-43)(www.xing528.com)

●功率谱密度 对所有ζ(t)的可能实现f(t)的功率谱密度P(ω)取统计平均

对于一般随机过程的谱密度，计算比较复杂。但当随机过程是广义平稳随机过程时，其谱密度与其自相关函数有关系，即维纳一辛钦(Wiener-Khinchin)定理。

定理2-5（维纳一辛钦定理） 广义平稳随机过程ζ(t)的自相关函数R(t)与功率谱P(ω)是一对傅里叶变换：

同时，由特殊情况

我们可以得到如下结论。

性质2-9 广义平稳随机过程ξ（t）中，每个时刻随机变量的方差等于该平稳随机过程的功率与均值平方的差。即记每个时刻所对应的随机变量均值为_μ，角频率功率谱密度为P（ω），则

注意，上面功率谱采用的是角频率表示，总是有个系数1／（2π），比较烦人，要想没有这个系数，可以采用线频率表示，此处从略。

一般把信号频谱取值非0范围在零频附近的那些信号称为基带信号，比如谱取值非0范围为[-W，W]；一般把信号频谱取值非0范围远离零频的那些信号称为频带信号（或带通信号），比如谱取值非0范围为[-W2，-W1]∪[W1，W2]，其中W1远大于0。

同时需要指出的是，一个信号的时域和频域的非零范围不可能同时有限，即至少其中之一是无限的，这个其实从傅里叶变换的“伸缩变换性质”也可略知一二了。在伸缩变换里，

可以看到时域展宽，则频域变窄；时域变窄，则频域展宽。而现实中，一般信号都是时域有限的，那么知其频域必然无限。