2.2.2方波信号和sinc信号——专访这对儿金童玉女

方波信号和slnc信号是两类简单但理论分析中经常用到的信号，一个是理想的窗函数或滤波器，一个是理想的捅值函数或脉冲信号，我们这里专门拿出一节来讲讲它们，以便后续能灵活应用。

性质2-7 定义标准单位方波信号为Rect(f)，

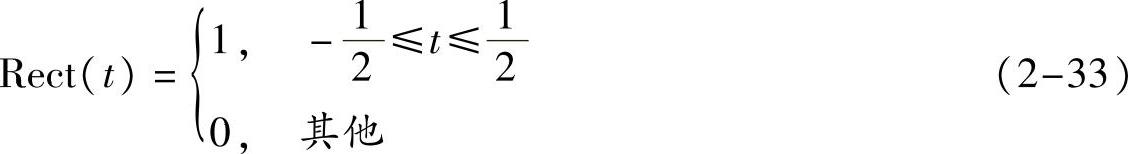
定义标准单位信号（t），

则有傅里叶变换对关系

本书后续内容中非标准单位方波都用标准单位方波的伸缩变换表示，例如，方波信号

f(t)=A， -τ≤t≤τ

可以表示成

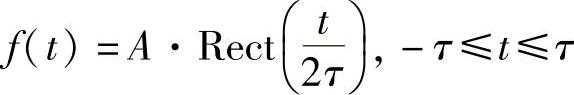
非标准单位slnc信号类似。另外，也可以看到Rect信号和slnc信号两者都是偶（实）信号。图2-5示意了一对方波信号和slnc信号。

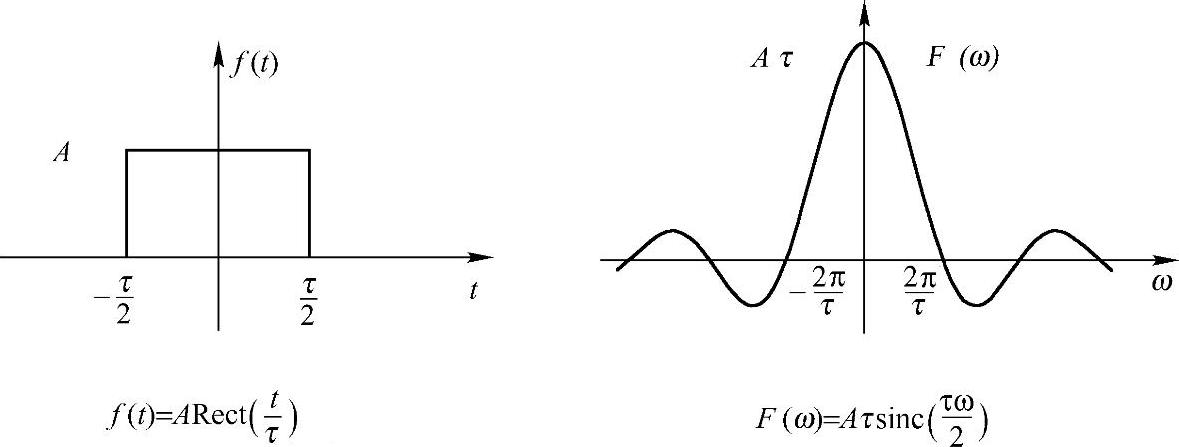
图2-5 方波信号与其傅里叶变换slnc信号

请大家仔细看一下图2-5．获取一些直观的特征，比如时域幅度和频域幅度的关系，时域方波持续时长与频域slnc信号零点位置关系等，熟练掌握这些对于以后灵活应用会有好处。我们先简单总结如下：

1)如果方波的持续宽度为7_，那么其傅里叶变换slnc信号中离坐标原点（零频）最近的零点离坐标原点距离为2π/τ，注意这是角频率：如果是线频率，距离就是1/τ，即倒数关系。

2)对于信号sinc(αt)，其离坐标原点最近的零点离坐标原点距离为π/α。

3)对于信号sinc(αf)，除了坐标原点附近的两个零点外，其他零点间隔为π/α。后续如果用到，我们就直接说两个零点的距离了，但请大家注意有这个特殊情况。

性质2-8（sinc信号能量） 首先方波信号的能量很容易求得，再由傅里叶变换的能量守恒性质．我们又可以得到slnc信号的能量

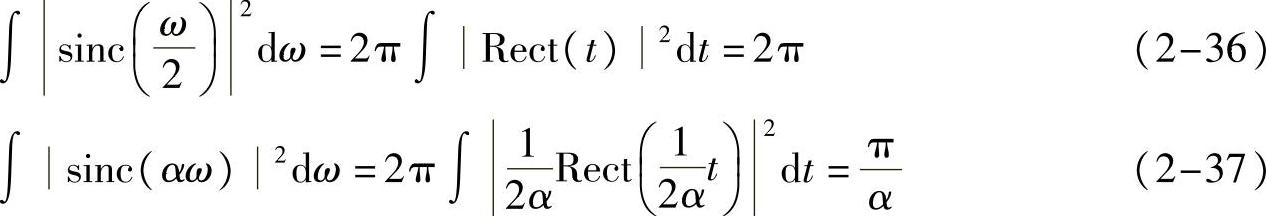
比较容易看到，截断的三角函数或复指数，，可以表示成如下形式：

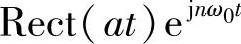
这样写的好处是可以省略关于自变量的取值范围声明，因为Rect（at）起到了这样的作用，相当于对信号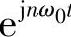加窗截取窗内的部分 所加的截取窗长为1/a显然对于其他区间截断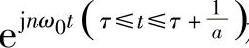相应平移窗函数Rect（at）即可，、(www.xing528.com)

根据前面性质2-4的讨论，我们知道当截断的长度为21T砌。的整数倍时，其构成一组正交基。即，当窗长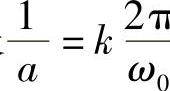时．Rect(at)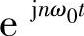为一组正交基。而根据傅里叶变换“时域旋转，频域平移”性质知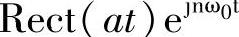，的傅里叶变换为

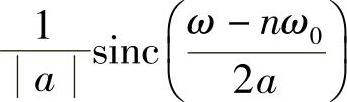
则当时，根据傅里叶变换作为一一线性映射把一组基变成另一组基，知此时信号序列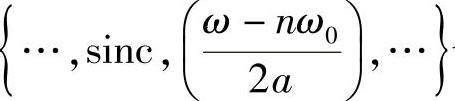也为一组正交基。特别地，取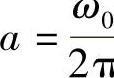代入，得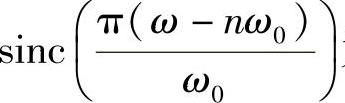为一组正交基。

定理2-4（sinc信号正交基） slnc信号序列

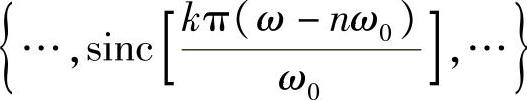
是一组正交基，其中k为某整数。即有

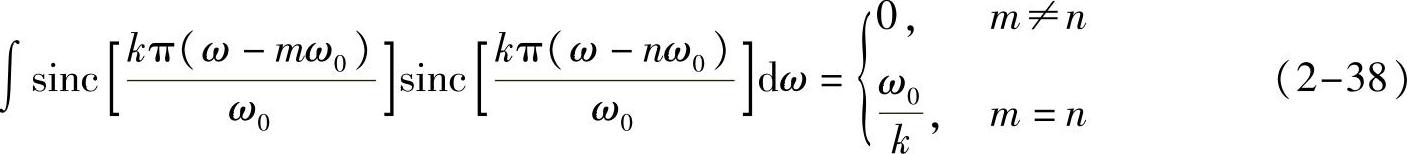
根据我们前面观察得到的smc信号的性质知，信号sinc[kπω/ω0]的零点之间的距离为ω0/k。而信号序列sin[kπ（ω-nω0）/ω0]，两两是相互平移nω0的关系，也即零点之间距离的整数倍关系。也就是说，相对于同一个smc信号，平移零点之间距离整数倍的信号（函数值可以伸缩变换）两两正交。如图2-6所示，虽然信号的正交需要看两个信号乘积的积分（信号常规内积）是否为0，这一般很难直观看出来，但图2-6中也或多或少有那么一点“正交”关系，比如一个信号在另一个信号的最大值点（即对应原点平移的那个）的取值都是0，大多数两个零点之间的函数曲线变化方向相反，等等。

这组slnc信号正交基也非常重要，稍后就会用到，先请大家熟悉留意一下。同样根据前面的讨论，我们知道定义存区间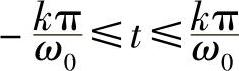上的“所有”信号f(t)可以由截断正交基表示为

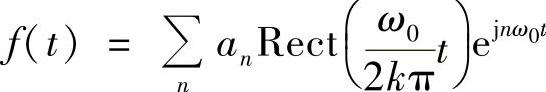
从而，这些信号f(t)的频谱可以由一系列频域slnc信号叠加出来，如图2-7所示，即

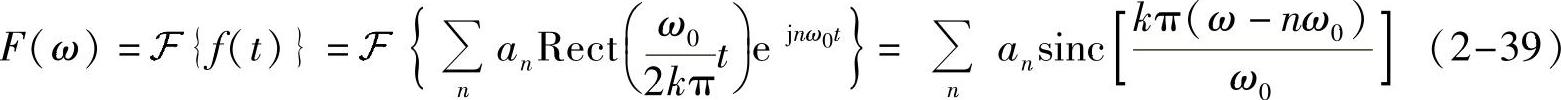
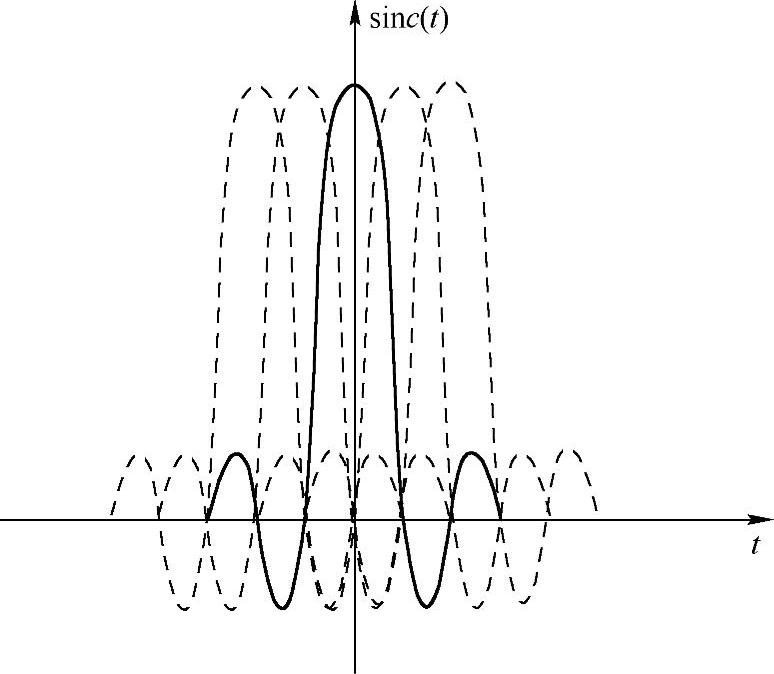
图2-6 slnc信号正交基

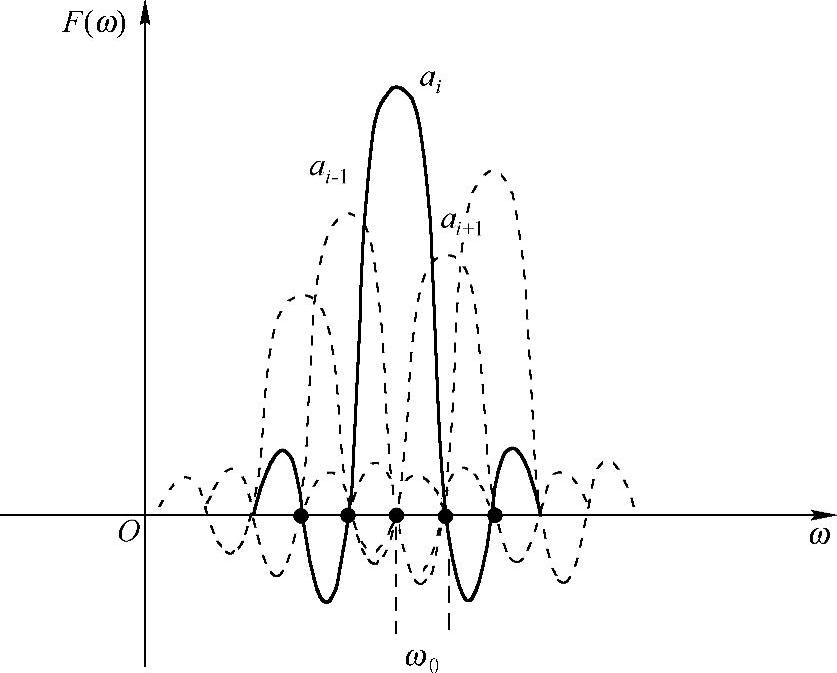
图2-7 信号频谱由slnc信号叠加出来

现在考虑，所有定义在区间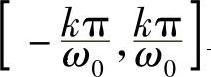上，但只有有限个正交基下的坐标可能非0的那些信号。不妨设仅在基向量

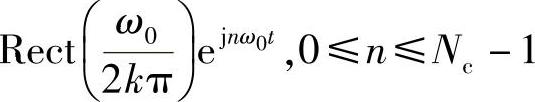
下的坐标an（0≤n≤Ne-1）可能不为0，其他基下坐标一定为0。那么，所有这些信号的频谱仅由有限个slnc信号叠加构成。想想，如果序列an，携带信息，把an表示的信号

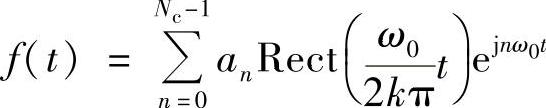
发送出去，接收端是不是很容易把an取出来？应该是的，因为接收端再重新计算各基下的坐标即可，这就是OFDM的最核心原理之一了，后面再详细讲解。