从傅里叶级数到傅里叶变换：晋级探究

注意性质2-4中，对于ω0没有任何限制，即使当角频率ω0→0时，如下集合中信号仍然是正交的：

也就是说“所有”在τ≤t≤τ+T0的信号都可以用它来表示（回忆前面刚讲过的先拓展，再由傅里叶级数展开，最后截断τ≤t≤t+T0那一截），其中T0=2π/ω0→+∞。而当T0→∞时，任何函数都可以看成是τ≤t≤τ+T0上的函数，从而任何信号都可以由该组信号来线性表示。那么，我们看看一个信号在这样一组基下的坐标是什么？仍然根据坐标计算公式，按部就班地计算在基信号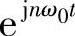下的坐标为

当ω0→0且n遍历(-∞,∞)时nω0可以排满整个角频率坐标轴ω,即任何一点ω总存在某个n使得ω=nω0那么f(t)在任何一个点ω=nω0所对应的基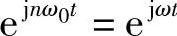下的坐标为

注意到一个信号在不同基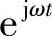下的坐标不同的是无穷小量dω以及常系数2π之外的那部分，我们就单独把那部分取个名字叫f（t）的傅里叶变换，记为

提醒

在基ωjωt下的实际坐标是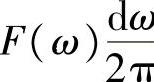，而不是傅里叶变换F（ω），切记！既然得到了坐标，显然信号f（t）可以表示成坐标与对应基的线性组合

这样的表示被称为F（ω）的傅里叶逆变换，记为

到此为止，我们就得到了傅里叶变换及逆变换。可以看到，弄来弄去，也还是按部就班地求某组基的坐标而已。所以，再给大家建议，一定要好好理解线性空间相关的理论，它才刚刚开始发挥作用，后续一直会用到。哪怕先把进度放一放，也请把那块知识掌握熟练。

上面的推导过程是对角频率来说的，如果采用线频率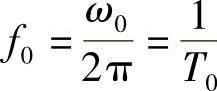，思想类似。只不过，这里转化为求如下这组基的坐标：

其实这组基和角频率是同一组基，只是表示形式上有点差异，导致线频率形式下的傅里叶变换略有差异。同样根据坐标计算公式知，当f0→0时，在基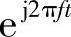下的坐标为

同样，注意df对于不同基是公共的，我们把剩下的部分称为线频率形式下的傅里叶变换，记为

接着线频率傅里叶变换讲，既然得到了坐标，则信号f（t）有线性组合表示

注意，这个就称为线频率形式下的傅里叶逆变换，和角频率形式上只有一个常量系数1/2π的差别。

定理2-3（傅里叶变换对）把如上讨论的信号f（t）和F（ω）记为一对傅里叶变换对，有(www.xing528.com)

采用线频率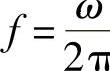表示的傅里叶变换对有

其中，角频率表示和线频率表示之间关系为

FL（f）=F（2πf） （2-30）

即把角频率表示自变量范围压缩2π倍就得到线频率表示。

本书后面的讲解可能只会基于其中一种形式说明，请读者朋友根据两者之间的这个关系自行思考同一个问题在另一种表示下是什么样子。当然，如果不会引起混淆，线频率表示FL（f）的下标L可以去掉。

性质2-5（能量守恒）同一能量信号的时域表示和频域表示，信号能量守恒，即

当然信号若是功率信号，那么就是时频域功率守恒。能量守恒可以看成模与坐标关系的简单应用，也即还是线性空间理论的简单应用，但它有个专门名称叫帕斯瓦定理(Parseval's Theo-rem)，详细推导说明见附录C。

和傅里叶级数一样，对于傅里叶变换，我们也有实信号频谱幅度对称性。

性质2-6（实信号频谱对称性）对于实信号，F（ω）*=F（-ω），从而∣F（ω）∣=∣F（-ω）∣，即幅度为关于原点对称的偶函数。

提醒

实信号频谱幅度对称性还说明，实信号的频谱的非零范围是关于原点（零频）对称的，比如非零范围为[-W，W]或者[-W2，-W1]∪[W1，W2]。所以，我们在后续讨论中，要画信号的频谱图时，总是画成对称的样子。还可以证明傅里叶变换和傅里叶逆变换都是线性映射，即

除了上面几个性质，傅里叶变换还有很多特殊的性质，以及特殊的变换对，基本上都可以根据傅里叶变换定义公式变形得到，具体内容见附录C。