周期信号的傅里叶级数

讲了傅里叶级数的故事，到底什么是傅里叶级数呢？相信大家都了解过，这里权当复习一下。绝大多数周期函数都可以表示成三角函数的无穷和形式。首先考虑较简单的函数值取值为实数的周期信号（实周期信号）f(t)，其一个正周期为T1>0，即F(t)=f(t+T1)。记对应线频率f1=1/T1，角频率ω．=2π/T1=2πf1。一般情况下，我们可以把它展开成不同频率的三角级数的和：

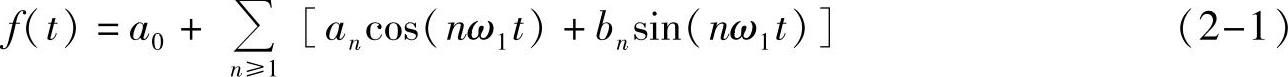
式(2-1)等号右边的和式被称为周期信号f(t)的傅里叶三角级数展开。对于实周期信号f(t)来说，系数an、bn都是实数，且是唯一的。特别地，系数n0被称为直流分量。

实际上，信号的傅里叶三角级数展开可以由线性空间知识来理解。但是，需要说明的是，本部分内容涉及的线性空间都是无限维空间，所以总是会出现一些特殊情况，在数学意义下不是严格完全正确的。对于这些特殊情况，并不影响我们对基本思想的理解，所以碰到时只给大家提醒一下，而不去把重点放在弄清楚这些特殊情况。因为实际中的大部分情况一般都会是满足正确条件的，或者说我们设计时就是让它满足正确条件的。

性质2-1 函数组

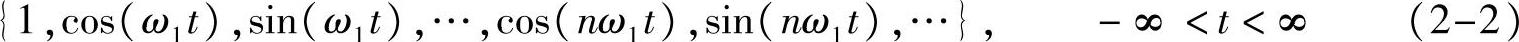
在函数的常规内积下是一组正交向量组，且构成“所有”^[1]周期为T/k或角频率为kω1实周期函数组成的线性空间的一组正交基,其中k＞0为整数。且有

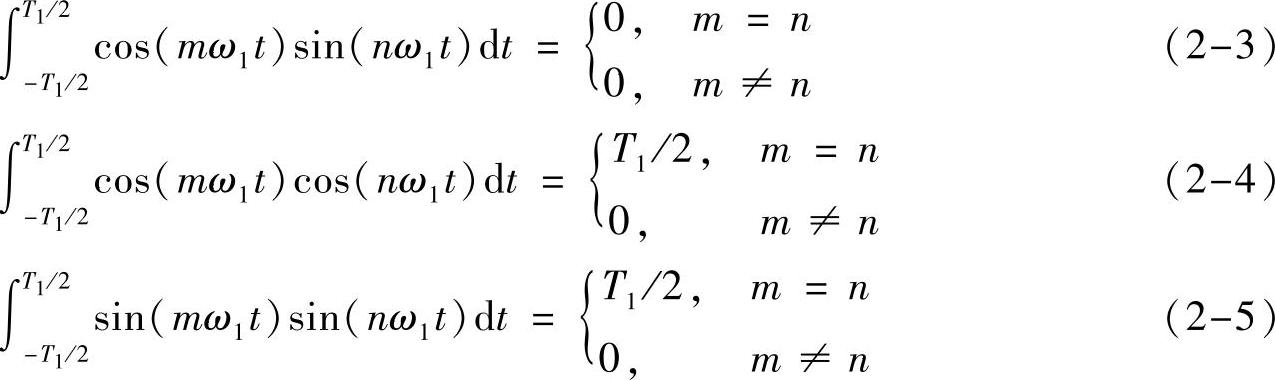
所以，如果周期信号f（t)的傅里叶级数展开存在，根据正交基下坐标计算方法，我们有

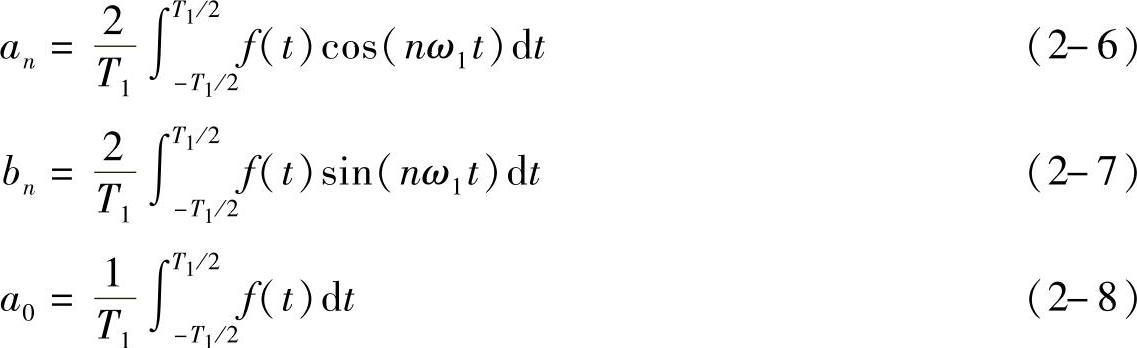
当一个周期信号能由式(2-2)的向量组表示出来，称该周期信号的傅里叶三角级数展开存在。那么，周期信号厂(t)的傅里叶三角级数展开存在是什么意思呢？应该是说对于任何一个点t，f(t)的值都等于其对应的傅里叶三角级数在点t的值。有没有可能虽然不是任何点都相等，但有一部分相等呢？要方便讨论这个问题，我们先定义信号f(t)确定的傅里叶级数（多数文献中直接称为f(t)的傅里叶级数）这个概念。

定义2-1（信号确定的傅里叶级数） 对于信号f(t)，不论其傅里叶级数展开是否存在，称如下级数为f(f)确定的傅里叶级数：

其中，系数a_n，b_n，a1分别由式（2-6）式（2-8）确定。

信号确定的傅里叶级数仅是一个临时的过渡概念，在没有进一步的证据之前，它和信号本身没有相等关系。

接着上面的问题，在哪些点f(t)与f(t)确定的傅里叶级数相等呢？狄利克雷(Dirichlet)给出了一个证据（或称为判断准则）。

定理2-1（狄利克雷充分条件） 设f(t)是以T为周期的周期函数。如果它满足以下条件：

●在一个周期内连续或只有有限个第一类间断点(第一类间断点指在那些点左右极限厂(￡+0)和f(t -0)都存在，但不相等的点）。

●在一个周期内至多只有有限个极值点。

则f(t)确定的傅里叶级数收敛，并且当f是f(t)的连续点时，收敛于f(t)；当f是f(t)的非连续点（第一类间断点）时，收敛于

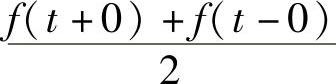
即满足狄利克雷条件的信号f(t)在其连续点等于f(t)确定的傅里叶级数，在非连续点不等。还请注意，狄利克雷条件只是其中一个证据，并不是唯一的准则，其他准则本书就不一一讲了。

很显然，注意到正弦函数是奇函数，那么当f(t)为偶函数且其傅里叶级数存在时，必然所有bn=0，即没有正弦分量（奇分量），那么对于这种情况f(t)实际上可以仅由余弦函数组合叠加得到；同理，当f(t)为奇函数且其傅里叶级数存在时，所有an=0，即f(t)实际上可以仅由正弦函数组合叠加得到。

再考虑，所谓级数收敛是什么意思呢？意思是说如下和式：

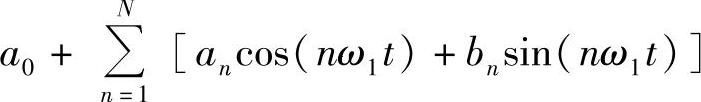
当N越来越大时，该和式和f（t）的误差越来越小。

下面简单举个例子看一下。

【例2-1】 考虑图2-1所示周期矩形波u（t）

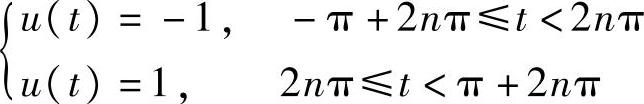
显然u（t）是奇函数，其傅里叶级数展开里只有如下正弦分量：

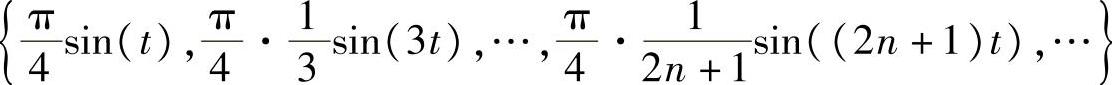
图2-1 周期信号u（t）

下面看取不同个数分量的逼近情况，如图2-2所示。

可以看到，随着分量项数的增加，和式越来越逼近信号u（t）；还可以看到，由于t是u（t）的一个非连续点，级数在t点收敛于

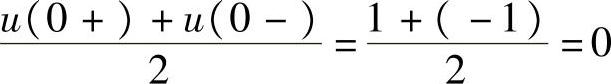
名人名言

数学大家高斯说，“如果一个人看到欧拉公式感觉不到她的优美，那么这个人基本上没什么数学才华了。”(www.xing528.com)

其实数学大师陈省身先生也这么说过，那就请大家一起来看看欧拉公式有多惊艳吧！

定理2-2（欧拉公式）

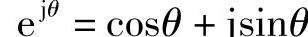
特别地，当θ=π时，得

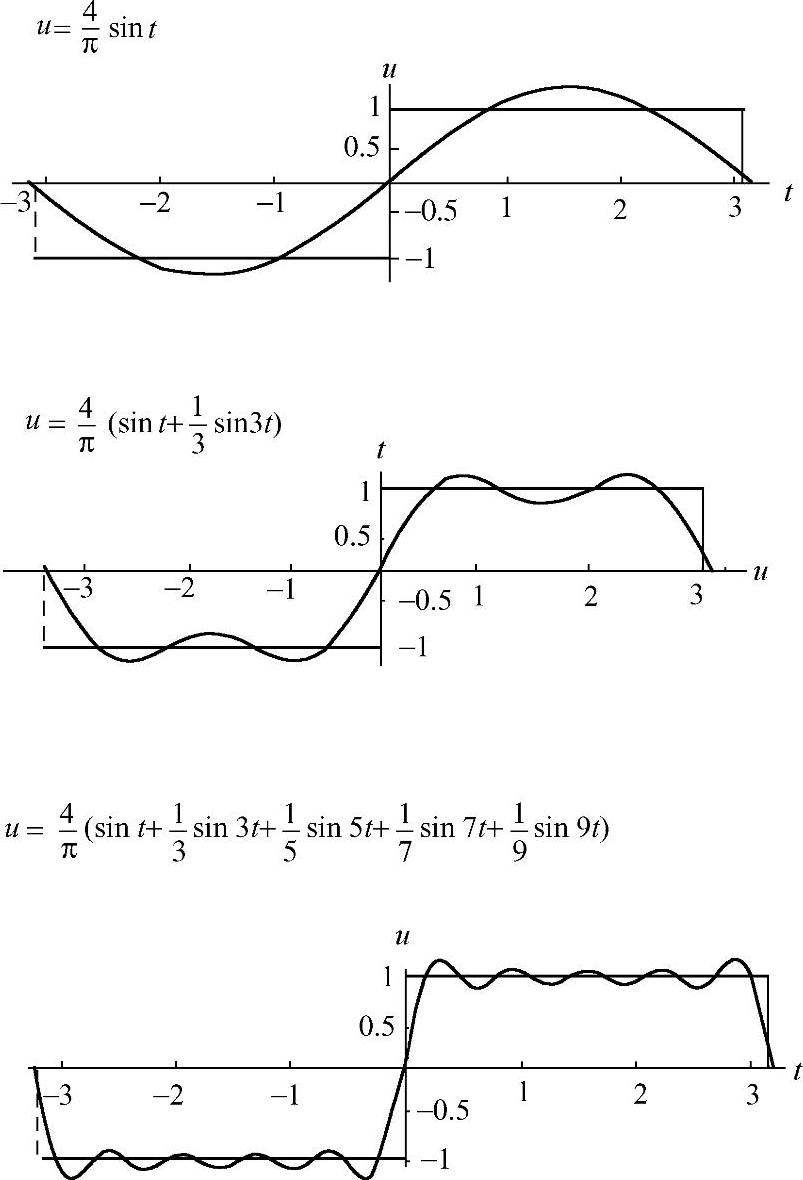
图2-2 展开项个数增加的不同逼近程度 ejπ=-1 (2-11)

其中几乎包含了所有特别的数e、j、π、1，确实非比寻常。应用欧拉（Euler）公式，我们知道

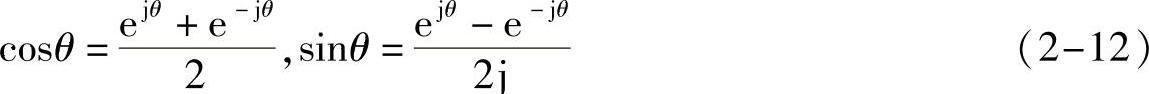
代入信号f（t）的三角函数形式傅里叶展开式（2-1），我们得到实信号f（t）的复指数形式傅里叶展开式

其中，

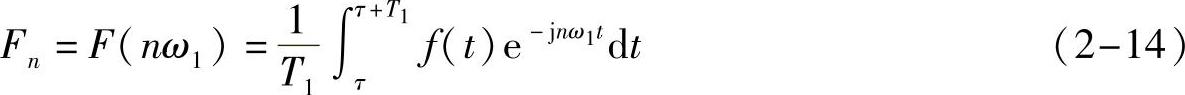
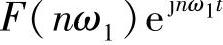一般被称为信号f（t）的n次谐波分量，相应系数Fn被称为n次谐波系数F_n一般为复数。

事实上，可以证明，如下复指数函数集合也构成一组正交组。

性质2-2 复指数函数集合

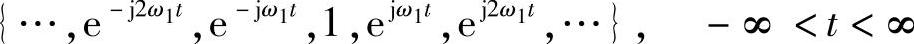
是一组正交向量组，且构成“所有”周期为T/k或角频率为kω的复周期函数组成的线性空间的一组正交基，其中k>0为整数。

注意，这个正交组不但能表示实信号，还能表示复信号（提醒：实信号是特殊的复信号），是对前面正余弦展开的扩展。有了这个基础，那么，仍然可以直接利用线性空间的知识，把任何一个讨论的复周期信号表示成该组基的线性组合，求相应坐标即可。由线性空间里的坐标计算方法，该线性空间中函数（作为向量看待）f（t）在基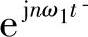下的坐标为

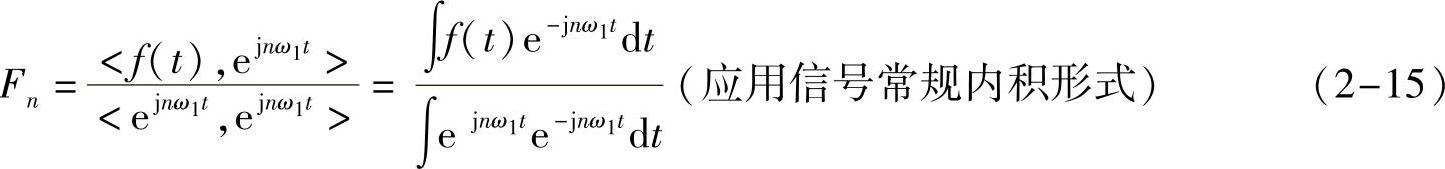
当然，这个坐标是唯一的。仍然有特殊周期信号不能由这组基表示，恕不深究。

另外可以看到，性质2-2对任何ω1都成立，即使当ω1→0时仍然成立，而当ω1→0，-∞＜n＜+∞时，nω1可以排满整个频率坐标轴ω，即任何一点ω总存在某个n使得ω=nω1。那么，可以知道在（-∞，+∞）上来看，任何两个不同信号ej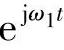和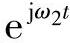都是正交的，

性质2-3（实信号谐波幅度对称性）如果f（t）是实信号，那么

即谐波分量幅度是关于正负频率对称的。

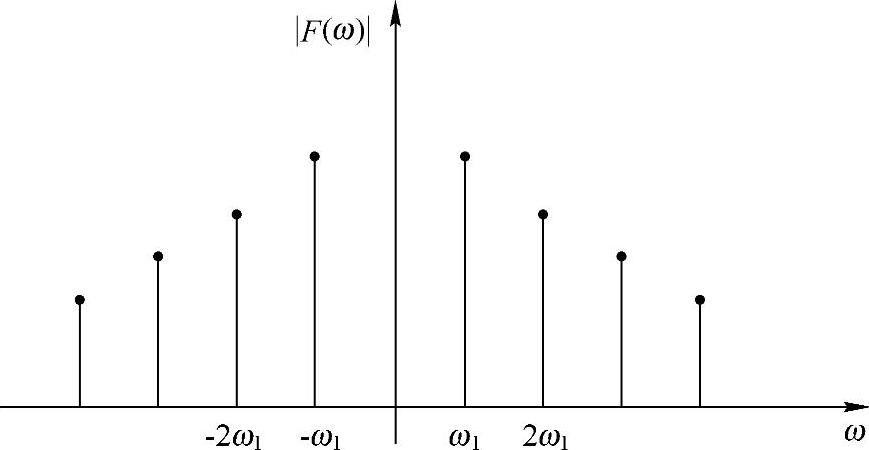
图2-3 实信号谐波幅度对称性

对于一般复信号，并没有这一幅度对称性质。为了描述简便，在不产生歧义的情况下，我们把以自然数e为底的复指数函数ejωt和真正的三角函数sin(ωt)，cos(ωt)都统称为三角函数，两者有差别的地方会单独特别说明。

思考一下，一个周期函数能表示成三角函数的和，即傅里叶级数展开存在，是说明每个点的函数值都是可以表示成该三角函数对应点的值之和。那这样的话，从周期函数中截取一段出来的时间有限函数，也相应地能表示成该三角函数同样截取后的函数和。也就是说，“任何”一个时间上长度为T1的函数，总是可以表示成角频率为ω1=2π/T1的三角函数的和。因为，总是可以先把该函数先拓展成一个以T1为周期的函数，求出其对应的傅里叶级数展开，最后再截取最开始的那个T1段。

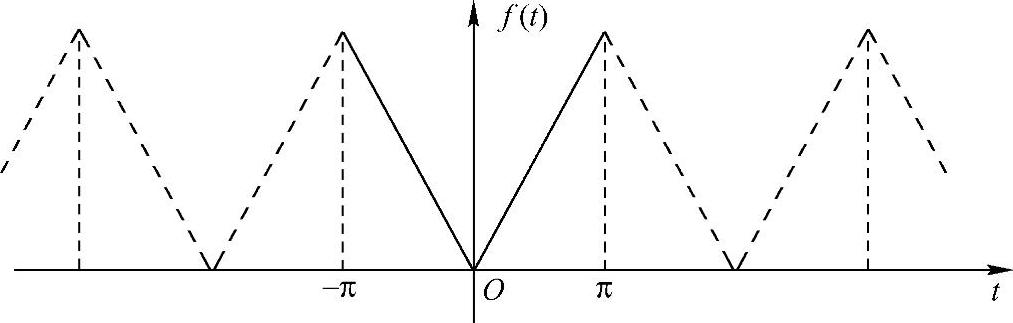
图2-4 非周期信号拓展成周期信号，T1=2π

上面的推理只能说明有限函数可以由有限三角函数表示，但是表示是不是唯一的呢？这个需要另外考虑。比如，假设周期函数f(t)的最小正周期为T1，现在截取比T1还短的一段，记其长度为T2。比T1还短的这一段函数形式上仍然可以表示成把F(￡)展开后对应的三角函数同样截取T2长那一段的和式展开。但是，可以证明，f(t)展开对应的三角函数截断后的T2长的那一段不是无关的，更不是一组正交基。也就是说，f(t)截断后的T2长函数虽然能表示成f(t)展开对应的三角函数同样截取T2长的函数和，但表示方法不是唯一的。那什么时候截断的三角函数是一组正交基呢？

性质2-4（截断三角正交基） 当T是T1=2π／ω1的整数倍时，如下形式的一组截断三角

函数是一组正交基：

“所有”定义在T0≤t≤t0+T0上的信号．f(t)都可以由它唯一线性表示出来。这一性质在后面我们还会经常用到，比如OFDM技术，从原理上讲（先不考虑如何对付无线信道等）只不过是该组基的简单应用而已。三言两语

既然信号已经有其他形式的表示形式，例如泰勒( Taylor)展开式等，为什么特别要展开成三角函数呢？因为泰勒展开式中，基函数xn是单调无界的，实现起来比较麻烦。而如果它操作的基本单元有简单的性质，比如周期的、有界的、只需要简单平移、简单相加操作等，就会简单一些，三角函数就满足这样的性质。