信号的简单表示：冲激分解

我们知道，生物学家解剖青蛙是为了做研究，物理学家从原子中分解出质子、中子、电子，也是为了做研究，化学家会将化学元素相互混合，还是为了做研究。原来分解与组合是做研究最基本的思想，研究信号也是一样。记一个信号为f(t)，那么能否把这个信号分解成更简单的信号组合呢？

最自然地，一个持续区间比较长的信号，总是可以看成是由很多区间比较短的信号一截一截地拼起来的。信号划分的区间越多，每个小区间持续的时间就越短，如图1-1所示。

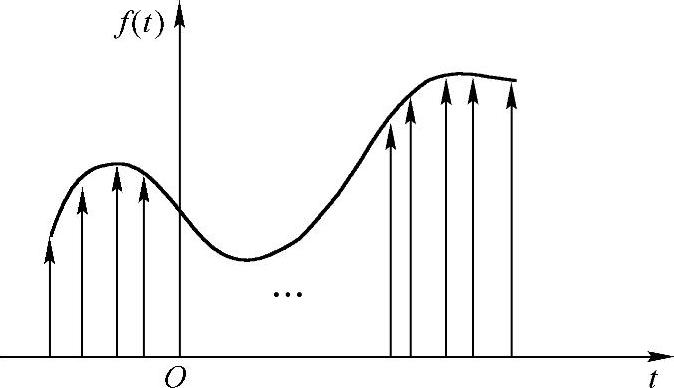
图1-1 信号f(t)被分解成持续时间趋于一点的信号构成

图1-1中，f(t）可以看成一系列持续区间非常短，几乎趋于一点的信号构成，而这样的不同小区间所示的信号都可以看成某个公共信号仅因为幅度不同伸缩而成的信号。那么，这个公共信号是什么呢？首先，定义这类通常被称为冲激信号(Dirac delta function)的特殊信号。

定义1-3（冲激信号） 满足如下几个条件的信号δ(t)，被称为冲激信号

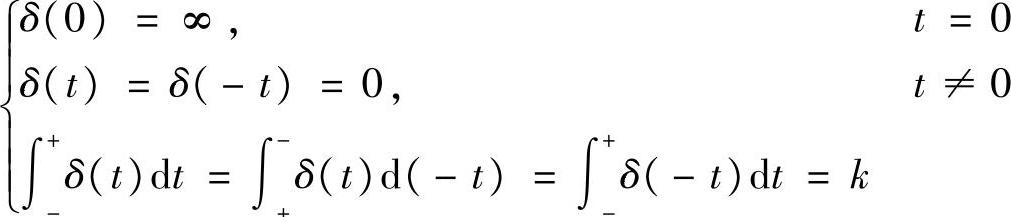
也许冲激信号看起来很奇怪，和一般的函数定义不一样，但我们先不严格地去探究该信号6(t)的数学意义（可能用到测度论等），有兴趣的读者自己去查阅相关资料。

冲激信号定义中的k称为冲激强度。对于k=l时的冲激信号，称之为单位冲激信号。后续为了记号简便，本书规定δ（f-t0）仅表示在t=t。时刻的单位冲激信号，非单位冲激信号（冲激强度为k）均表示成kδ（t-t0）的形式。

下面看看任何信号表示成单位冲激信号的严格形式是怎样的。

性质1-1（信号的冲激表示） 任何信号f(t)可以表示成不同时刻的冲激信号的无穷和（积分）

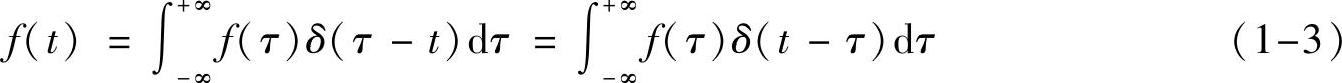
可以看到，任何信号厂(t)都可以写成f(t)与冲激信号δ(t)的卷积形式（卷积及推导见附录C），而这只是任何信号一个比较自然直观的分解形式。当然，你还可以发挥想象把信号分解成其他简单信号的合成，只要这样分解有意义，能够带来某些好处即可。例如，后面我们将会看到的分解成sinc(t)信号、指数信号ejwt等。如果你的分解形式不能带来任何好处，那就只是你自己的思考理解过程，最多就相当于一个习题：如果你的分解形式能带来很大的好处，并且别人从来没有发现过，那这就将成为知识，成为定理流传下去。(www.xing528.com)

这就是研究，这大概就是人类知识的形成过程。先要有最基本的思想，比如这里的把复杂的东西分解成简单东西的思想：接下来就是基本思想的具体体现了，这里就是具体怎么分解了，可能某些人一下子在某种背景下，某种需求下，找到了一个特有用的基本思想的具体体现形式，那么这个具体形式就成了基本定理。后续可能有很多人沿着这条路深入下去，就形成了这条路的知识体系。你会发现，知识的形成是有选择性的，那么多条路，最后留下来的只是几个特别的分支，不排除当初选择其他分支，可能人类的知识体系会发展得更先进、更深刻。同时，对于那些发现某条路并得到承认的人除了天分和努力，也多多少少需要一些运气的。

下面，我们把式(1-3)所定义的信号的冲激表示做一个简单的应用，看看能得到什么结果。

性质1-2（冲激信号能量）单位冲激信号的能量满足

证明：利用式，特别地，我们看看取f（t）δ（t）时有什么结果

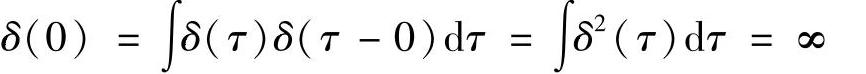
由此得证。

从该结论中，我们可以看到冲激信号的能量为无穷大，并且等于δ(0)，很好奇这个无穷大到底有多大呢？人有三教九流，无穷大也该有个高低先后。话说康托的集合论有很大的篇幅就是研究如何把无穷大也像自然数1，2，3，…那样，大小关系定义得清清楚楚。比如，所有自然数组成的集合{1，2，3，…}中的元素个数为无穷大，显然自然数集合的所有子集组成的集合中元素个数也为无穷大，它们一样大吗？回到我们的问题，冲激信号的能量对应的无穷大有多大？怎么刻画呢？那就再挖掘一下吧。

性质1-3 冲激函数δ(t)在t=0的取值δ(0)是与微分量的倒数等价的无穷大量，即

说明一下，微分量可能在不同地方用不同的字母表示，但所有相互独立的变量对应的徽分量是等价的：当然，如果两个变量不是独立的，而是满足某种关系，比如变量w和变量f满足∞=2πf，那么显然dω≠df，而是dω=2πdf请把这点分清楚，不要迷糊。

上面几节内容所讲的信号能量、功率，以及相关运算等定义适用于确定信号。稍微扩展一点：一般我们讲函数都是指确定性的函数，即一个自变量对应的函数值一定是一个唯一确定的值。后续研究巾可能涉及一些不确定性的东西，就是说有一个信号，但是这个信号具体是什么是不确定的，我们只知道它可能是很多个信号中的一个，并且每一个以一定的概率出现。那怎样来处理这类广义信号呢？更准确的数学描述，要从概率论和随机过程开始。这部分内容，我们放到本书附录B关于概率基础的内容里讲，有兴趣的读者，可直接转到那里继续。