设计原理和方案的优化

在大多数的长距离数字通信中，一个基本问题是在接收端以正确的频率和相位产生一个时钟，这样数据可以被正确解码。时钟通常是从接受到的数据中推导出来的。

传统上是利用模拟电路（例如锁相环）来进行时钟恢复，但是它们易受时间和温度飘移的影响。另外，这样的电路在包含脉冲串传输的应用中是不合适的，因为它们响应慢，对于那些超过一个数据率的应用也是不合适的。

输入数据流通常是在发射端被量化（在空闲周期里提供时钟信息），然后被编码，每一个码代表一个符号。然后码以所谓的符号率发射。接收端的任务就是恢复符号时钟。

图8.1.1给出了时钟恢复的原理。数据流延时半个时钟周期后和它自身做模2相加（即异或），产生一个输出（在点C处），它包含依符号率改变的电平。接着将数据加到一个边缘稳定的带通无限冲激响应滤波器。这样的一个滤波器的冲激响应随时间衰减得非常慢，在滤波器的中心频率ω₀处产生一个“阻尼振荡”。即使在一个合理长度的时间内输入数据流中没有传输，边缘稳定滤波器也能确保有一个输出。滤波器的抽样频率选择为符号率的倍数。期望的符号时钟是利用过零检测（见图8.1.1的点E处）从滤波器的输出中推导出来的。对于2的补码表示，这可以通过检验数字滤波器输出端数据样本的符号而轻易实现。

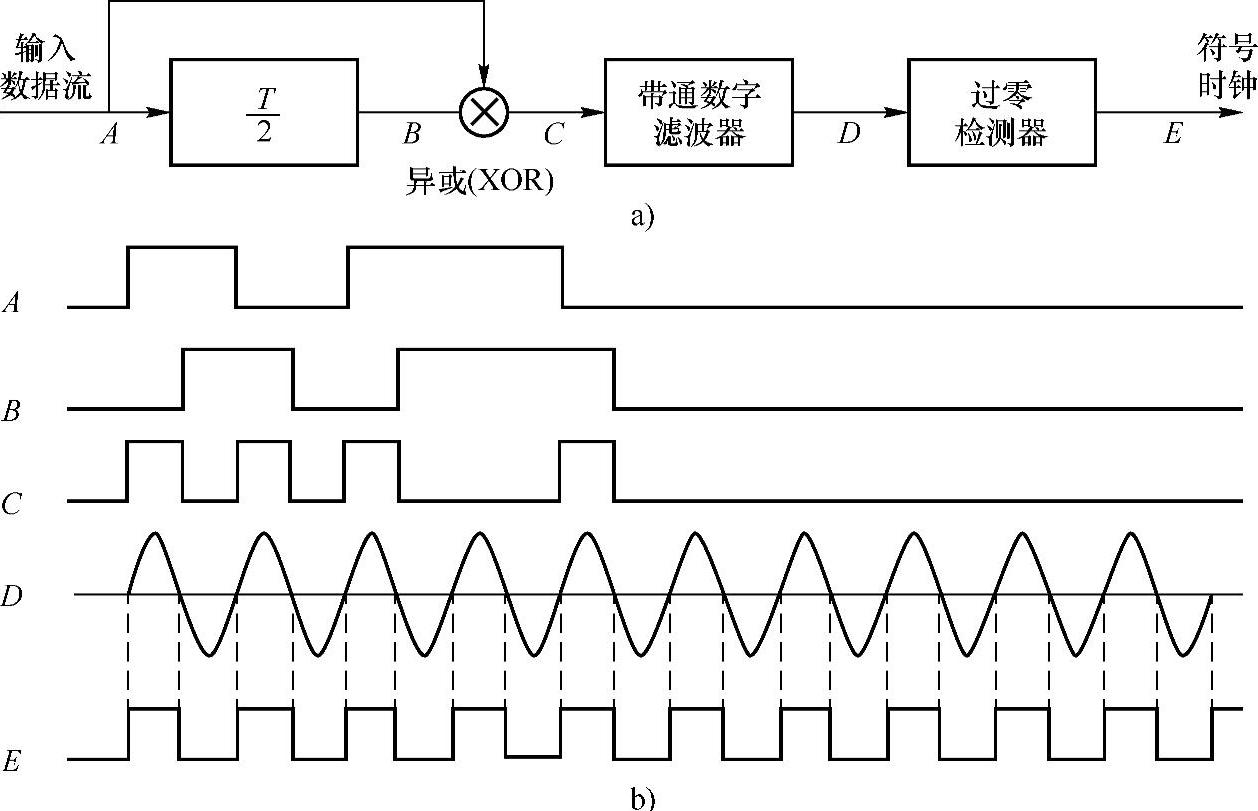
图8.1.1 数据通信中符号时钟恢复的原理图

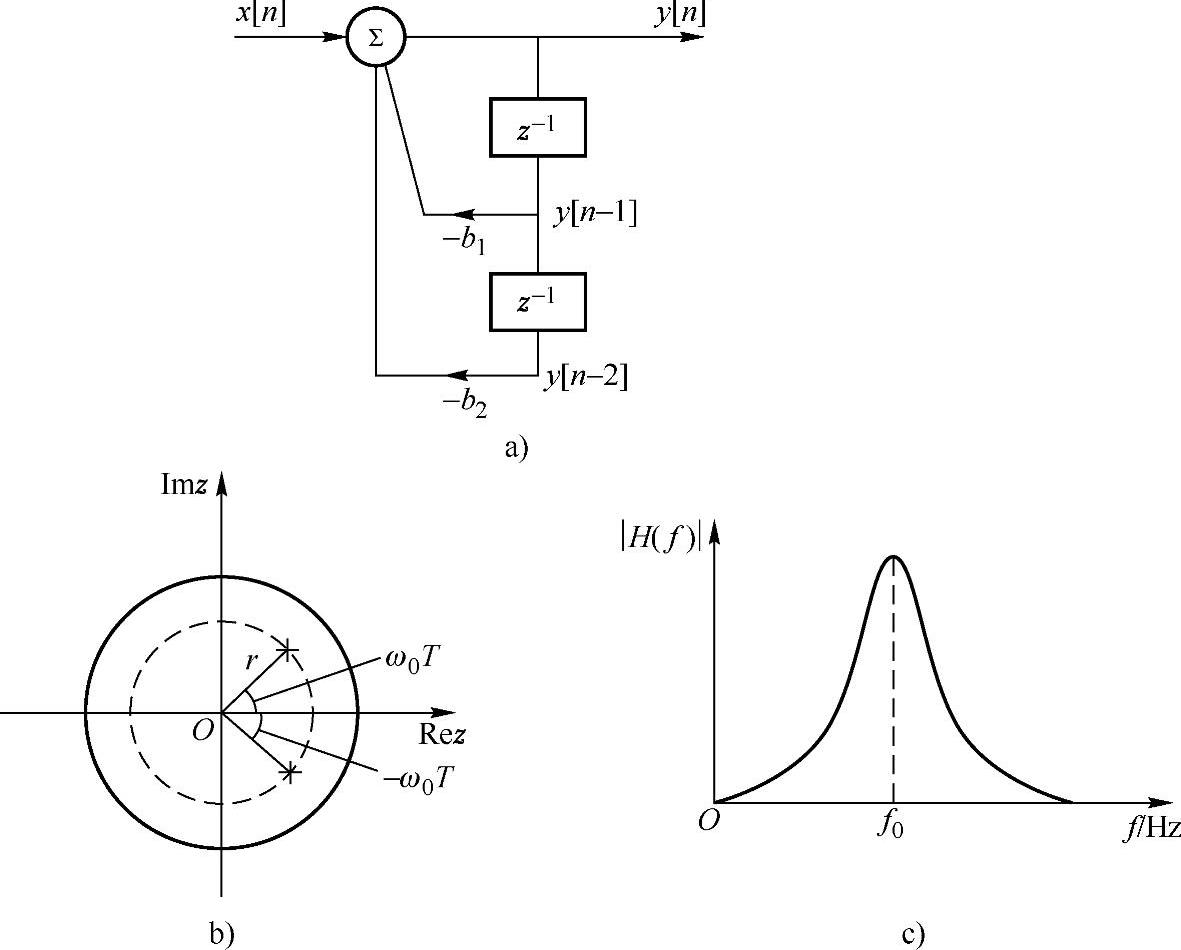
图8.1.2所示的简单的全极点无限冲激响应滤波器可以用来做符号时钟恢复，滤波器的特性由下面的系统函数给定，即

(www.xing528.com)

图8.1.2 简单全极点IIR滤波器

a）符号时钟恢复的IIR滤波器的结构 b）极点图 c）滤波器的频谱

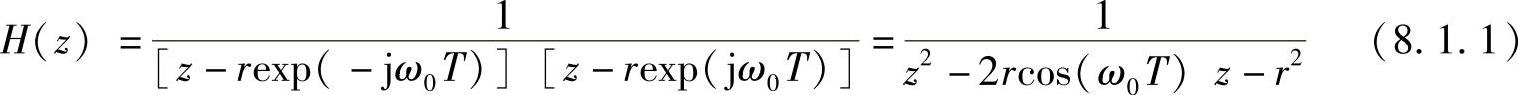
式中，ω₀是带通滤波器的中心频率；r是极点的半径；T是抽样周期；ω₀通常选择为等于或非常接近待恢复的符号时钟频率；抽样频率是中心频率的倍数。滤波器的带宽是由极点的半径决定的。为了确保冲激响应是随时间缓慢衰减，极点通常放置在非常靠近单位圆的地方，通常在0.99＜r＜1的范围内。极点半径r和滤波器带宽B有如下关系，即

r≈1-（B/f_s）π （8.1.2）

式中，f_s=1/T是滤波器的抽样频率。