FIR滤波器：实验原理与方法说明

FIR滤波器的设计问题在于寻求一系统函数H（z），使其频率响应H（e^jω）逼近滤波器要求的理想频率响应H_d（e^jω），其对应的单位抽样响应h_d[n]。

1.用窗函数设计FIR滤波器的基本方法

设计思想：从时域出发，设计h[n]逼近理想h_d[n]。设理想滤波器频率响应H_d（e^jω）的单位脉冲响应为h_d[n]。以线性相位FIR数字低通滤波器为例。

h_d[n]一般是无限长的，且是非因果的，不能直接作为FIR滤波器的单位抽样响应。要想得到一个因果的有限长的滤波器h[n]，最直接的方法是截断h[n]=h_d[n]w[n]，即截取为有限长因果序列，并用合适的窗函数进行加权作为FIR滤波器的单位脉冲响应。按照线性相位滤波器的要求，h[n]必须是偶对称的。对称中心必须等于滤波器的延时常数，即

用矩形窗设计的FIR数字低通滤波器，其幅频特性在通带和阻带都呈现出振荡现象，且最大波纹大约为幅度的9%，这个现象称为吉布斯（Gibbs）效应。为了消除吉布斯效应，一般采用其他类型的窗函数。

2.典型的窗函数

（1）矩形窗（Rectangle Window）

w[n]=R_N[n] （7.6.4）

其频率响应和幅频特性分别为

（2）三角形窗（Bartlett Window）

其频率响应为

（3）汉宁（Hanning）窗

其频率响应为

（4）海明（Hamming）窗

其频率响应为(www.xing528.com)

（5）布莱克曼（Blankman）窗

其频率响应为

（6）凯塞（Kaiser）窗

式中，β是一个可选参数，用来选择主瓣宽度和旁瓣衰减之间的交换关系，一般来说，β越大，过渡带越宽，阻带越小衰减也越大；I₀（·）是第一类修正零阶贝塞尔函数。

若阻带最小衰减表示为A_s=-20log₁₀δ_s，β的确定可采用下述经验公式，即

若滤波器通带和阻带波纹相等即δ_p=δ_s时，滤波器节数可通过下式确定，即

式中，。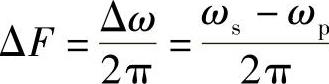

3.利用窗函数设计FIR滤波器的具体步骤

1）按允许的过渡带宽度Δω及阻带衰减A_s，选择合适的窗函数，并估计节数N，其中A由窗函数的类型决定。

2）由给定的滤波器的幅频响应参数求出理想的单位抽样响应h_d[n]。

3）确定延时值。

4）计算滤波器的单位抽样响应h[n]，h[n]=h_d[n]w[n]。

5）验算技术指标是否满足要求。