实验原理：使用FFT对序列进行末尾补零扩展

1.快速傅里叶变换（FFT）算法

长度为N的序列x[n]的DFT为

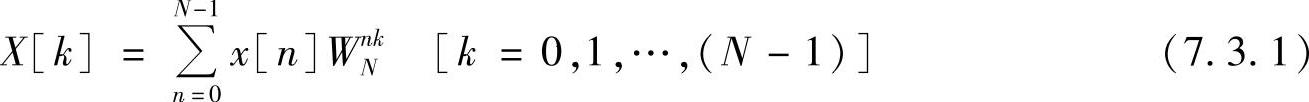
N点的DFT可以分解为两个N/2点的DFT，每个N/2点的DFT又可以分解为两个N/4点的DFT。依此类推，当N为2的整数次幂时（N=2^m），由于每分解一次就会降低一阶幂次，所以通过m次的分解，最后全部成为一系列2点DFT运算。以上就是按时间抽取的快速傅里叶变换（FFT）算法。当需要进行变换的序列的长度不是2的整数次方的时候，为了使用以2为基的FFT，可以用末尾补零的方法，使其长度延长至2的整数次方。

序列的离散傅里叶逆变换为

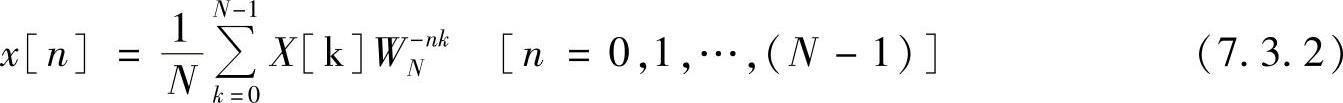
离散傅里叶逆变换与正变换的区别在于变W_N为W_N^-1，并多了一个1/N的运算。因为W_N和W^-1_N对于推导按时间抽取的快速傅里叶变换算法并无实质性区别，因此可将FFT和快速傅里叶逆变换（IFFT）算法合并在同一个程序中。

2.利用FFT进行频谱分析

若信号本身是有限长的序列，计算序列的频谱就是直接对序列进行FFT运算求得X[k]，X[k]就代表了序列在（0～2π）之间的频谱值。(www.xing528.com)

幅度谱为

相位谱为

若信号是模拟信号，用FFT进行谱分析时，首先必须对信号进行采样，使之变成离散信号，然后就可按照前面的方法用FFT来对连续信号进行谱分析。按采样定理，采样频率应大于2倍信号的最高频率，为了满足采样定理，一般在采样之前要设置一个抗混叠低通滤波器。用FFT对模拟信号进行谱分析的框图如图7.3.1所示。

图7.3.1 用FFT对模拟信号进行谱分析的框图