理想采样过程的原理与推导

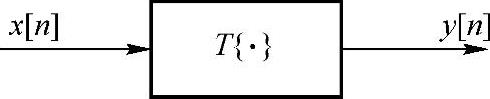
图7.2.1 离散时间系统

1.离散时间系统

一个离散时间系统是将输入序列变换成输出序列的一种运算。若以T{·}来表示这种运算，则一个离散时间系统可由图7.2.1来描述。

输出与输入之间的关系可用下式表示

y[n]=T{x[n]} （7.2.1）

离散时间系统中最重要、最常用的是线性移不变系统。

2.离散时间系统的单位脉冲响应

设系统输入x[n]=δ[n]，系统输出y[n]的初始状态为零，这时系统输出用h[n]表示，即h[n]=T{δ[n]}，则称为系统的单位抽样响应。可得到

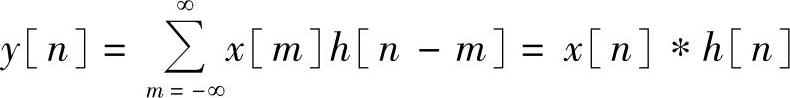
该式说明线性移不变系统的响应等于输入序列与单位抽样序列的卷积和。

3.连续时间信号的采样

采样是从连续信号到离散时间信号的过渡桥梁，对采样过程的研究不仅可以了解采样前后信号时域和频域特性发生的变化以及信号内容不丢失的条件，而且有助于加深对拉普拉斯（Laplace）变换、傅里叶（Fourier）变换、z变换和序列傅里叶变换（即离散时间傅里叶变换）之间关系的理解。

对一个连续时间信号进行理想采样的过程可以表示为信号与一个周期冲激脉冲的乘积，即

式中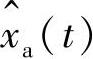，是连续信号的理想采样；δ_T（t）是周期冲激脉冲，即

(www.xing528.com)

设模拟信号x_a（t），冲激函数序列δ_T（t）以及抽样信号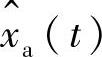的傅里叶变换分别为X_a（jΩ）、M（jΩ）和，即

X_a（jΩ）=F{x_a（t）} （7.2.4a）

M（jΩ）=F{δ_T（t）} （7.2.4b）

根据连续时间信号与系统中的频域卷积定理，式（7.2.2）表示的时域相乘，变换到频域为卷积运算，即

由此可以推导出

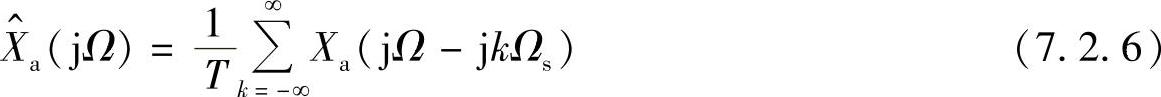
式中，T是采样周期，Ω_s=2π/T。由此可知，信号理想采样后的频谱是原来信号频谱的周期延拓，其延拓周期等于采样频率。根据奈奎斯特采样定理，如果原信号是带限信号，且采样频率高于原信号最高频率的2倍，则采样后的离散序列不会发生频谱混叠现象。

4.有限长序列的分析

对于长度为N的有限长序列，只观察、分析在某些频率点上的值。

一般只需要在0～2π之间均匀的取M个频率点，计算这些点上的序列傅里叶变换，即

式中，ω_k=2πk/M（k=0，1，…，（M-1）；X（e^jω）是一个复函数，它的模就是幅频特性曲线。