等波纹逼近法优化有限冲激响应数字滤波器设计

从数值逼近的理论角度来看，窗函数法设计有限冲激响应数字滤波器属于均方误差最小的逼近，而频率抽样法设计有限冲激响应数字滤波器属于插值法逼近，它保证在取样点ω_k与理想特性H_d（e^jω）完全一致，在其他非取样点上H（e^jω）是插值函数φ（ω，k）的线性组合。这两种逼近方法有一共同的缺点，就是在整个要求逼近的区间（0，π）内误差分布是不均匀的，特别是在幅频特性具有跃变点的过渡区附近误差最大。等波纹逼近是利用切比雪夫逼近理论，使其在要求逼近的范围内，误差分布是均匀的，所以也称为最佳一致意义下的逼近。与窗函数法及频率抽样法相比，当要求滤波特性相同时，阶数就可以比较低。

H_d（e^jω）与H（e^jω）分别是理想与实际设计的滤波器频率特性，H_d（e^jω）的频率特性容差图如图6.5.1所示，在0≤ω≤ω_p范围内最大误差为δ₁；在ω_s≤ω≤π范围内，最大误差为δ₂。H（e^jω）的图形如图6.5.2所示，H_d（e^jω）与H（e^jω）之间的误差如图6.5.3所示，这一误差具有等波纹分布特性。切比雪夫等波纹设计就是要求在0～π区间内使最大误差最小化。为了统一使用最大误差最小化的准则，通带和阻带内的误差统一表示成加权误差函数，定义加权误差为

E（ω）=W（ω）[H_d（e^jω）-H（e^jω）] （6.5.1）

式中，W（ω）为误差加权函数，有

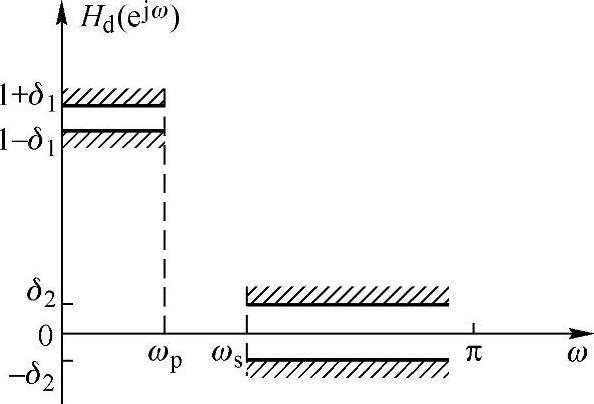
图6.5.1 低通滤波器的误差容限

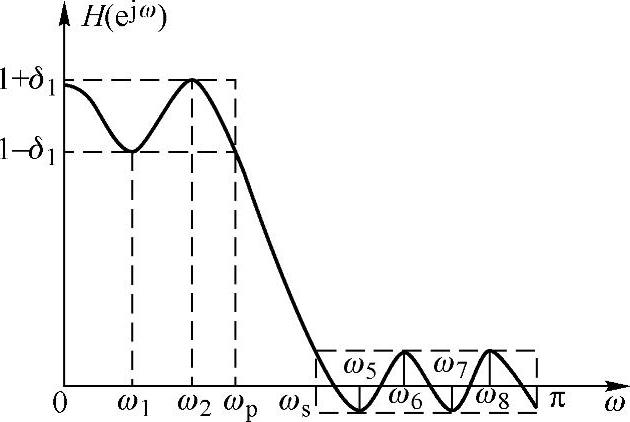
图6.5.2 实际设计低通滤波器的频率特性

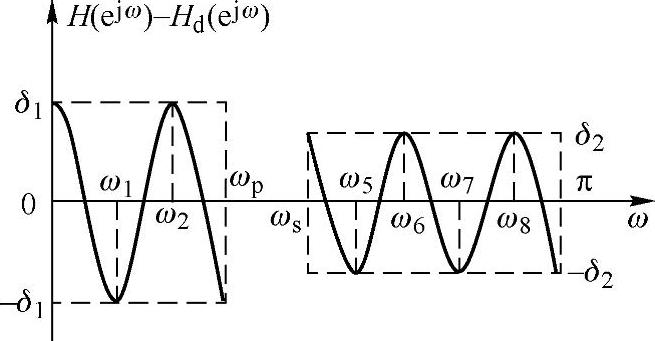
图6.5.3 H（e^jω）与H_d（e^jω）之间的误差

式（6.5.2）表明，在允许误差比较大的地方，例如图6.5.3所示情况，通带误差比较大，此时用较小的权函数；在误差要求小的地方用较大的权函数。这样，切比雪夫等波纹设计问题就是要求出H（e^jω），使其在实现逼近的各个频带上（包括通带和阻带），误差函数E（ω）的最大绝对误差达到最小，如果用‖E（ω）‖来表示这个最小值，则有

式（6.5.3）也意味着使δ₂为最小。

根据线性相位频率特性的一般表示式，为了分析简单而又不失一般性，设滤波器的单位抽样响应为h[n]，其频率特性具有零相位，即

式中，假设N为奇数，并令，则有

由于用等波纹逼近，其误差函数的极值点也就是H（e^jω）的极值点，考虑到cos（nω）是cosω的各次幂之和，即

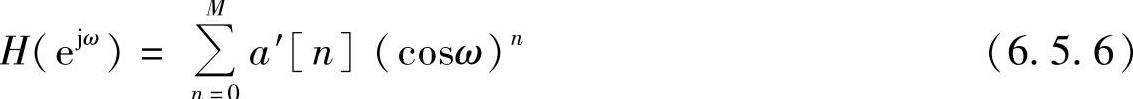
因而给定M、H（e^jω）的极值点数目，可以对H（e^jω）求导得到，即有

式（6.5.7）表示求和对象为M-1次多项式，因而共有M-1个根，再加上sinω中的0和π两个根，H（e^jω）共有M+1个极值，除ω=0和ω=π外，其余M-1个极值可以根据需要安排在通带和阻带内。例如图6.5.2所示为N=15的情况，除去ω=0和ω=π必须为极值外，对其余6个极值点，在通带内安排两个，阻带内安排四个。

根据线性相位频率特性对极值数目的约束，等波纹设计共有M，δ₁，δ₂，ω_s，ω_p五个参数需要确定。根据选择的参数不同可以有不同的逼近方法。

1970年由赫尔曼（Herrman）和舒斯勒（Schuessler）提出固定参数M、δ₁、δ₂，允许ω_s、ω_p改变，从而导出等波纹滤波器设计的非线性方程，即在M-1个极值频率处取H（e^jω）的值为1±δ₁（通带内）或±δ₂（阻带内），各阶导数在这些频率处为零。例如对图6.5.2所示的情况，有

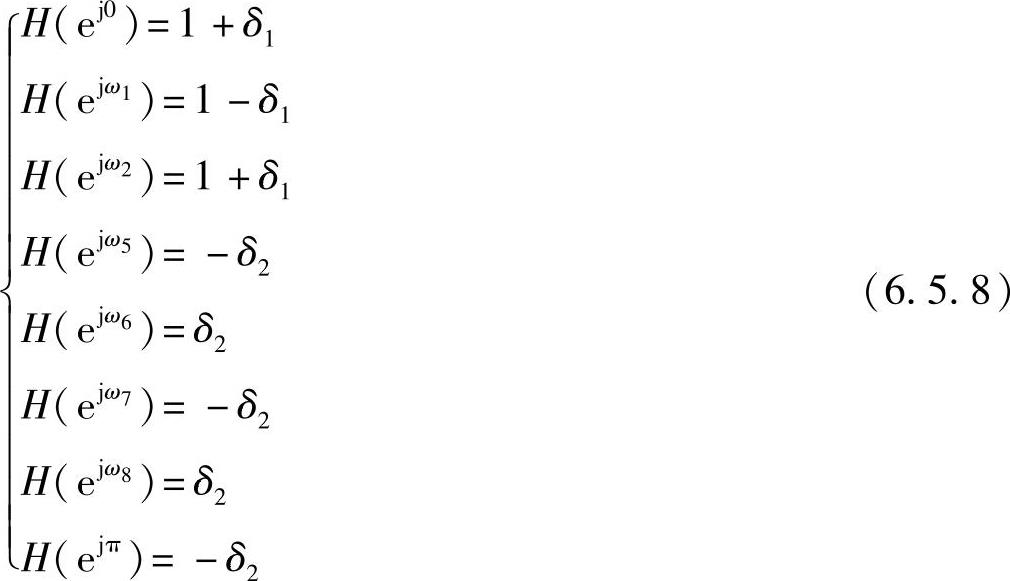
此外，在各极值点的导数应等于零，即有

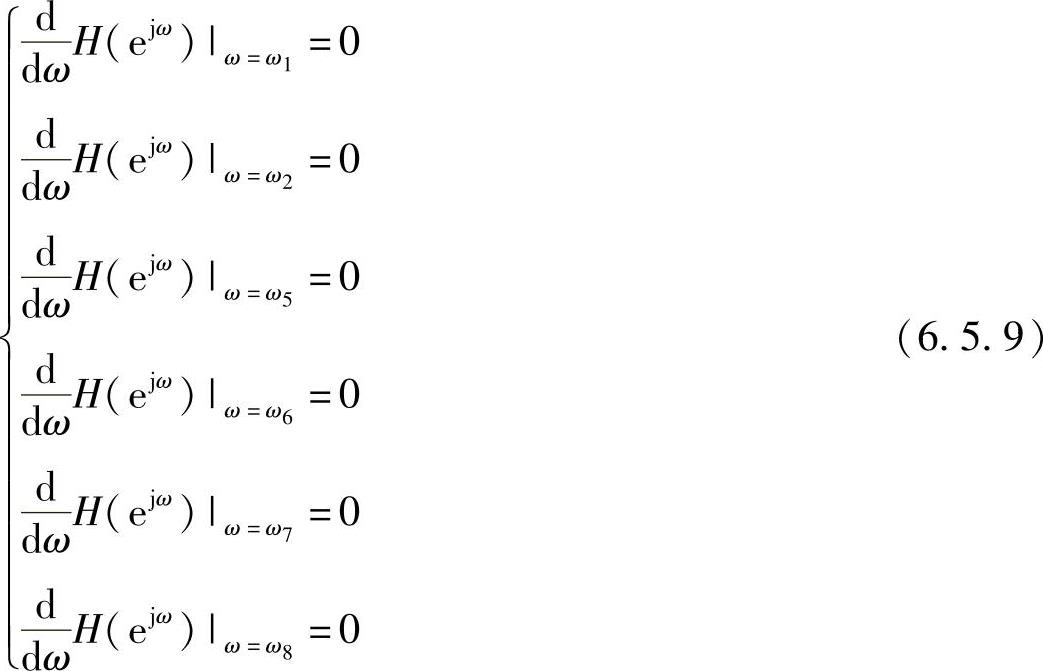
这两组联立方程共有（M+1）+（M-1）=2M个方程，所以可以解出M-1个未知频率和M+1个a[n]系数。这是一组非线性方程，一般用Fletcher-Powell算法迭代求出。

这种等波纹设计方法的主要缺点是要解一组非线性方程，因而适用于M值较低的情况。另外由于只是根据N及δ₁、δ₂来设计，因而过渡带ω_s和ω_p无法控制，所以不够灵活。

为了克服以上设计的缺点，1972年Parks和McClellan将切比雪夫逼近理论中的“交替定理”用于等波纹滤波器的设计中。当“交替定理”用在等波纹有限冲激响应数字滤波器设计中时，定理可以这样表述：设F为闭区间0≤ω≤π的任一闭子集，为使式（6.5.4）的H（e^jω）在F上成为H_d（e^jω）唯一最好的逼近，其充要条件是，函数E（ω）在F上至少有M+2个变号，且E（ω_i）=-E（ω_i-1）=±‖E（ω）‖=maxE（ω），其中ω₀≤ω₁≤ω₂…≤ω_M+1，所有ω_i属于F。这一定理不仅说明H（e^jω）的存在唯一性，而且指出构造H（e^jω）的具体方法。(www.xing528.com)

根据“交替定理”假设已知F上的M+2个交错频率为ω₀，ω₁，…，ω_M+1，则由式（6.5.1）得

式中，a[n]和δ₂都是待求的参数。式（6.5.10）可以表示为矩阵形式，并把a[n]简化写作a_n，有

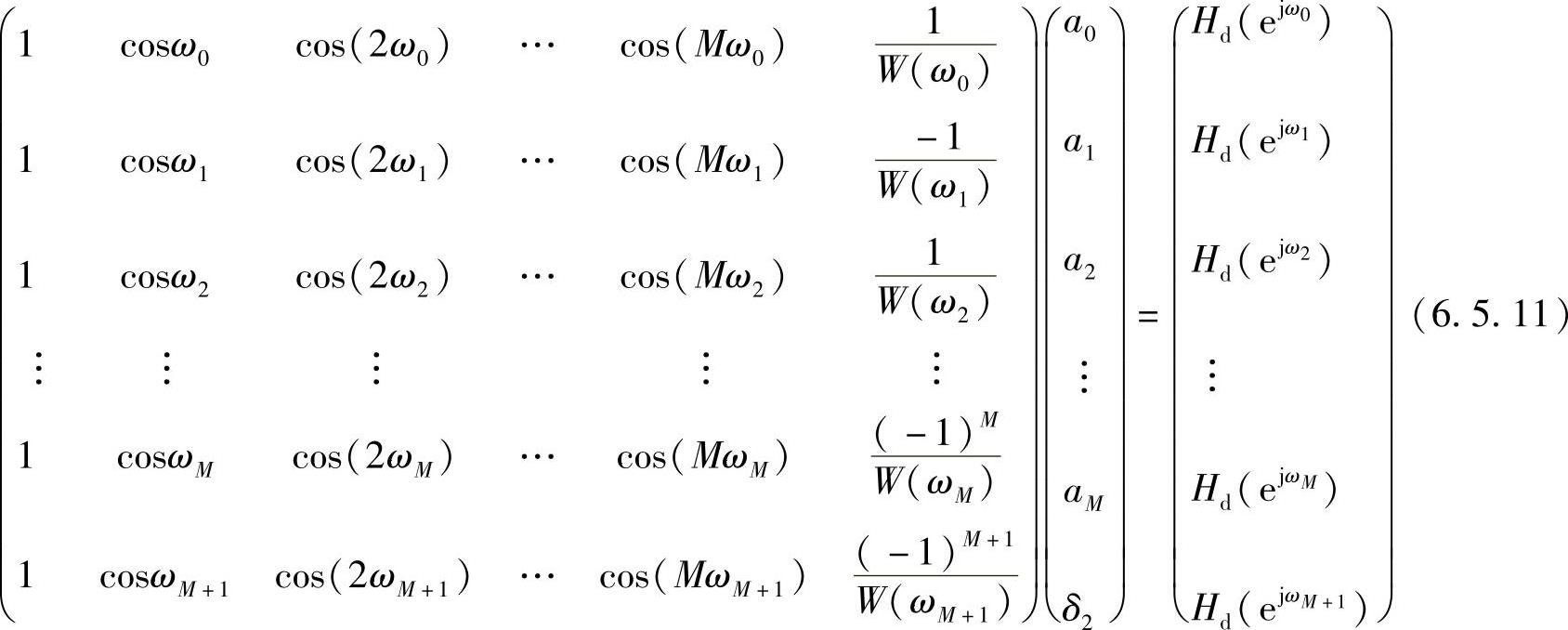
解式（6.5.11）方程组，可以唯一地求出系数a_i[i=0，1，…，（M+1）]及偏差δ₂，这样即可构成最佳逼近滤波器H（e^jω）。

在这里需要说明的是，根据H（e^jω）的极值点约束条件，共有M+1个极值，而式（6.5.11）表示的方程组要求有M+2个交错频率，实际上在过渡带处的两个频率ω_s和ω_p都可以达到极值，即

因此ω_s和ω_p也是属于F集中的两个频率，这样，满足“交替定理”的频率共有M+3个，所以这时设计的滤波器称为“超波纹”滤波器。“超波纹”的含义是指把ω_s和ω_p也包括在极值频率范围内，因此它比原来要求的极值个数M+2多了一个。用这种方法设计的滤波器实际上是指定M、ω_s、ω_p，而使误差δ₁和δ₂达到最小。如果要求的δ₁和δ₂值是已知的，那么为了算出预定的δ₁和δ₂滤波器，可以固定ω_p，改变ω_s，重新进行设计计算，直到满足提出的δ₁和δ₂为止。

解式（6.5.11）表示的方程组是困难的，因为所有极值事先是不知道的。通常用数值分析中的Remez算法，靠逐次迭代来求出要求的极值频率。这种算法有下列几个步骤：

第一步：首先在频率子集F上等间隔取M+2个频率ω_i[i=0，1，…，（M+1）]作极值频率的初始猜测值，然后用下式求出δ₂，即

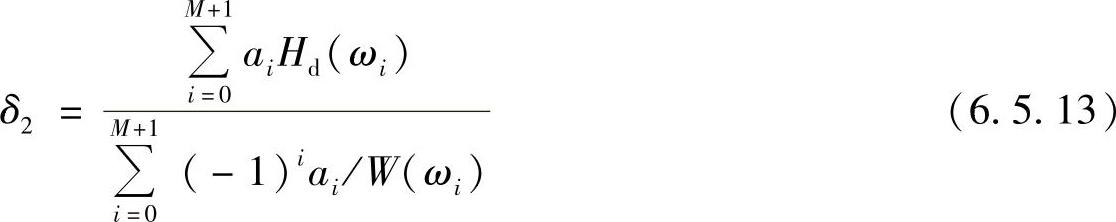
式中

把ω_i[i=0，1，…，（M+1）]代入式（6.5.14），求出δ₂，这就是第一次指定极值频率的偏差值。

再由δ₂并利用重心形式的拉格朗日插值公式得到H（e^jω），即

式中

把求得的H（e^jω）代入式（6.5.1）的误差表示式中，得到误差函数E（ω）。如果这样得到的E（ω）在所有频率上都能满足E（ω）≤δ₂，则说明δ₂是波纹的极值，且ω₀，ω₁，…，ω_M+1的初始猜测值是交错点组频率，计算即可结束。但实际上第一次不会恰好如此，总有某些频率使E（ω）＞δ₂，因而需要进行第二步。

第二步：在第一步找出的使E（ω）＞δ₂的那些频率附近，找出局部极值点，用这一局部极值频率代替原来初始猜测频率，这样又得到一组新的交错点组频率，根据式（6.5.13）重新计算δ₂，且求出H（e^jω）和E（ω），这就是新一轮迭代。

如此重复迭代，由于每次新的交错点频率都是E（ω）的局部极值点，因此按式（6.5.13）计算的δ₂是递增的，但最后收敛到δ₂自身的上限，此时H（e^jω）也就最佳一致地逼近H_d（e^jω）。若再进行一次迭代，E（ω）的峰值将不会大于δ₂。到此迭代即告结束，对H（e^jω）求离散傅里叶逆变换从而得到要求的h[n]。

以上算法的示意图如图6.5.4所示。设图中第一次极值频率估计不合适，计算出来的δ₂太小，因而按上列迭代步骤第二步寻求局部极值频率，这样必须在通带和阻带内取较密的频率分割点，从而收索找出峰值点，以此作为新的一组交错点组频率。图6.5.5画出了Remez交换算法的流程图。这种交换算法的计算机程序可以在有关的参考书中找到，这里不再赘述。

Remez交换算法占用内存较少，运算时间短，效率高。实践表明，如果初始估计极值频率点为均匀分配，那么一般只需五次左右迭代即可找到要求的极值频率。

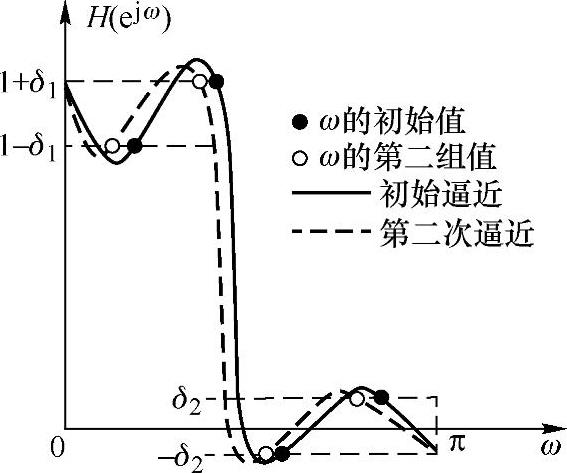
图6.5.4 Remez交换算法示意图

等波纹设计中可控制的参数是δ₁、δ₂、ω_p、ω_s，而滤波器长度N需事先给定，通常用下列近似公式来估计滤波器长度，即

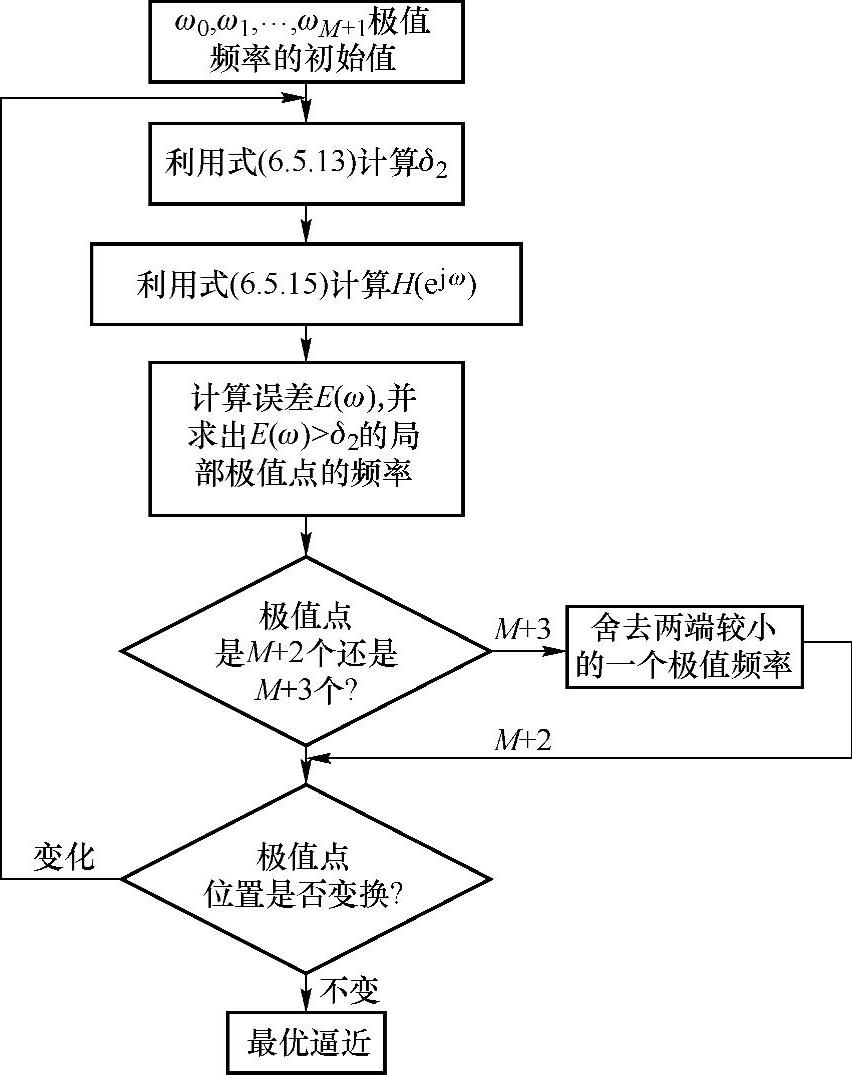
图6.5.5 Remez算法流程图