设计线性相位有限冲激响应数字滤波器

用频率抽样法设计线性相位滤波器时，也应注意频域样本H[k]的幅度和相位，其抽样值H[k]的幅度和相位一定要满足前面所讨论的四类线性相位滤波器的约束条件。

1）第一类线性相位滤波器，即h[n]偶对称，长度N为奇数时，其频率特性为

幅频函数具有偶对称性，即

H（ω）=H（2π-ω） （6.4.7）

如果频域样本H[k]也用其幅值和相角来表示，则有

H[k]=H_ke^jθ[k] （6.4.8）

根据式（6.4.7）和式（6.4.8），则有

H_k=H_N-k （6.4.9）

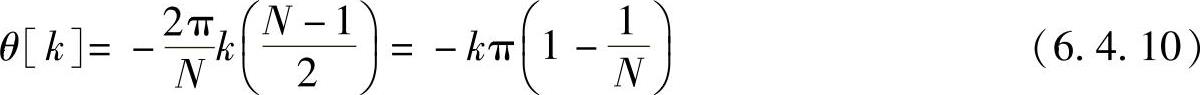
2）对于第二类线性相位有限冲激响应数字滤波器，即h[n]偶对称，N为偶数，其幅频函数H（ω）关于ω=π是奇对称的，关于ω=0、2π为偶对称

H（ω）=-H（2π-ω） （6.4.11）

所以，这时的H_k也应满足奇对称要求

H_k=-H_N-k （6.4.12）

相位仍然满足

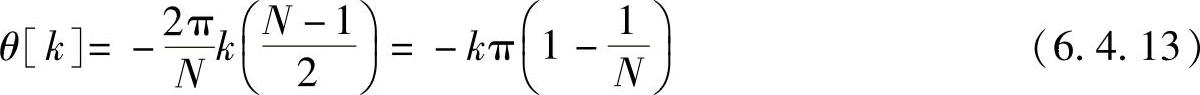
3）对于第三类线性相位有限冲激响应滤波器，即h[n]奇对称，N为奇数，可有

H_k=-H_N-k （6.4.14）

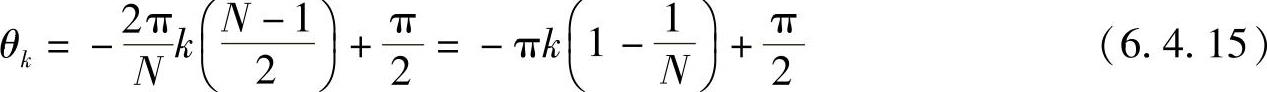
4）对于第四类线性相位有限冲激响应数字滤波器，即h[n]奇对称，N为偶数，可有

H_k=H_N-k （6.4.16）

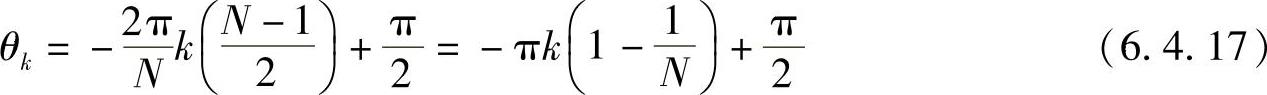
频率抽样法的特点：优点是可以在频域直接设计，并且适合最优化设计；缺点是抽样频率只能等于2π/N的整数倍，或加上π/N，因而不能确保截止频率ω_c的自由取值，要想实现自由地选择截止频率，必须增加抽样点数N，但这又使计算量加大。

频率抽样法设计有限冲激响应滤波器步骤如下：

1）根据阻带衰减指标确定过渡带自由变量个数。

2）根据过渡带宽确定数据长度。

3）对理想滤波器抽样。

4）采用优化方法计算过渡带自由变量的取值。

5）计算h[n]或直接由频域内插公式求H（ω）。

6）验证指标。若达不到要求则重复1）～6）。

值得指出的是：本方法与前面讨论的频率抽样结构并没有因果关系。频率抽样结构适合任何有限冲激响应数字滤波器；而频率抽样法设计的滤波器也可采用前述的任何结构来实现。(www.xing528.com)

【例6.4.1】 用频率抽样法设计一线性相位数字滤波器，N=15，幅度抽样值为

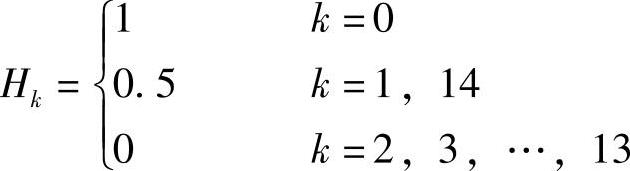
试设计抽样值的相位θ_k，并求h[n]及H（ω）的表达式。本例的单位抽样响应见图6.4.2。

解 因本题所给N=15，且H_k=H_N-k满足偶对称条件，由H₀=1可知，这是第一类线性相位滤波器。相位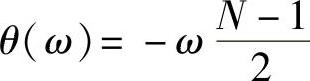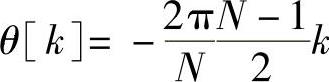，，因此有

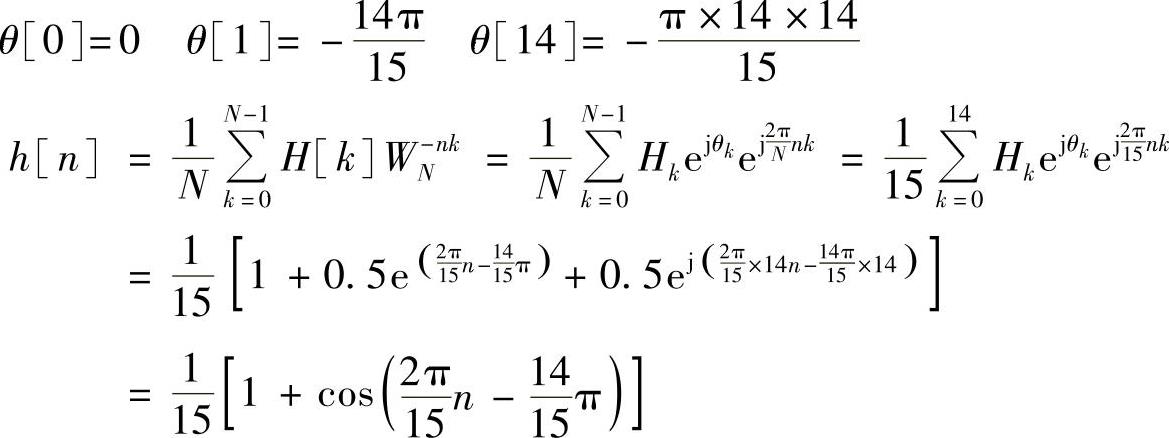
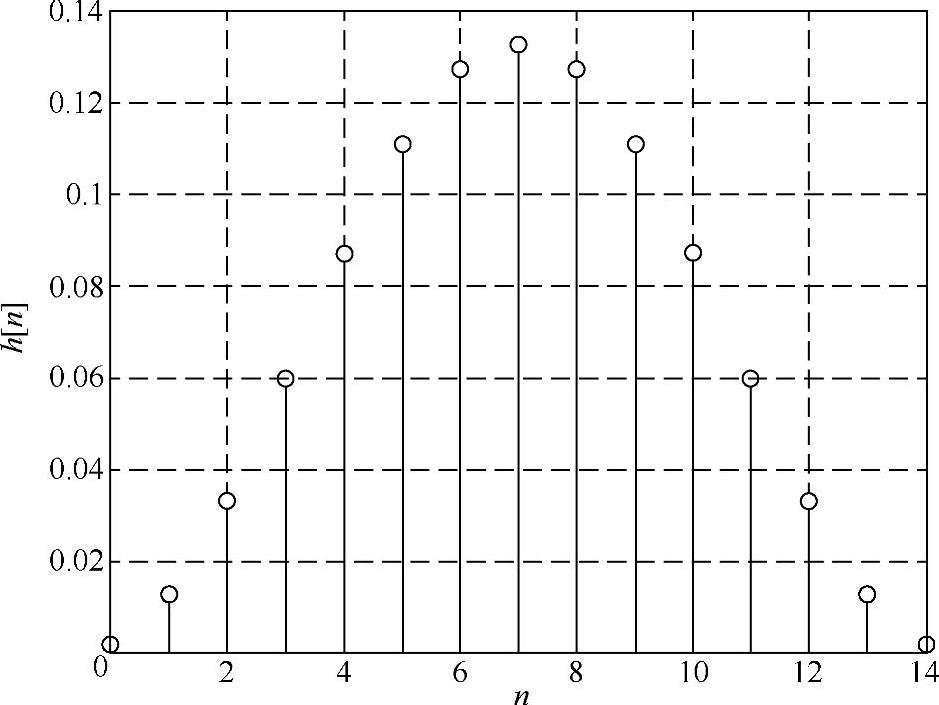
图6.4.2 例6.4.1的单位抽样响应

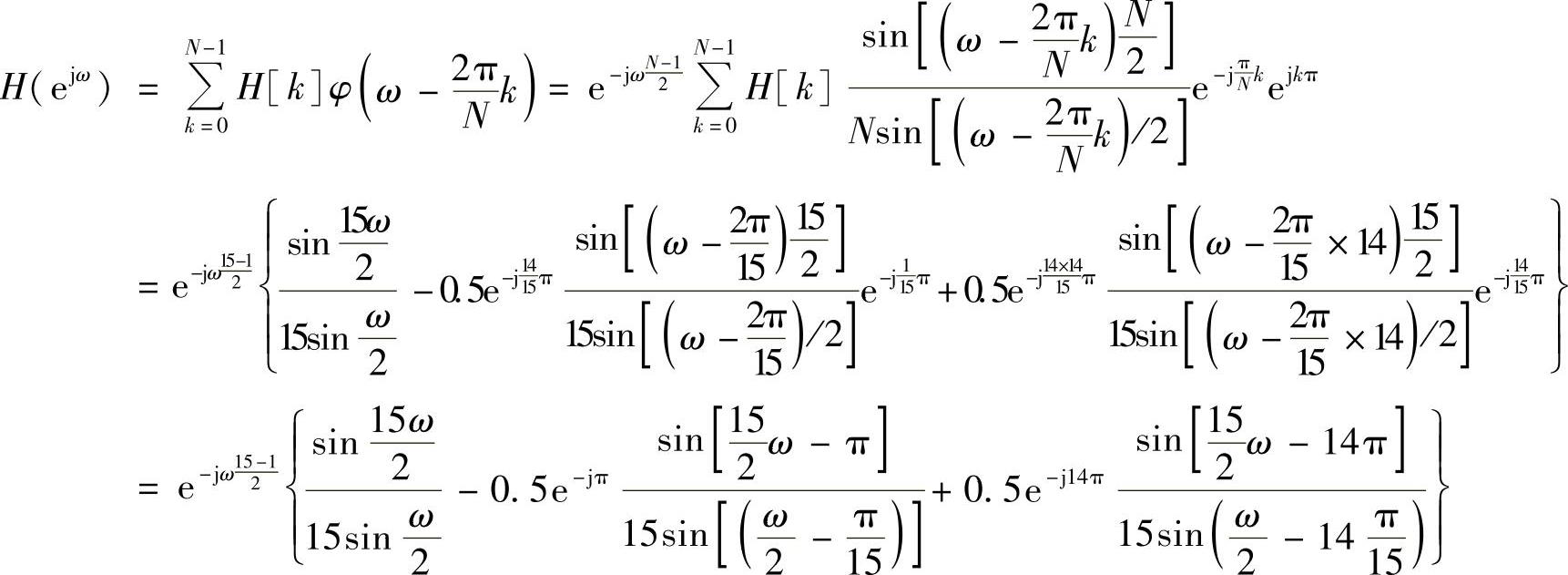
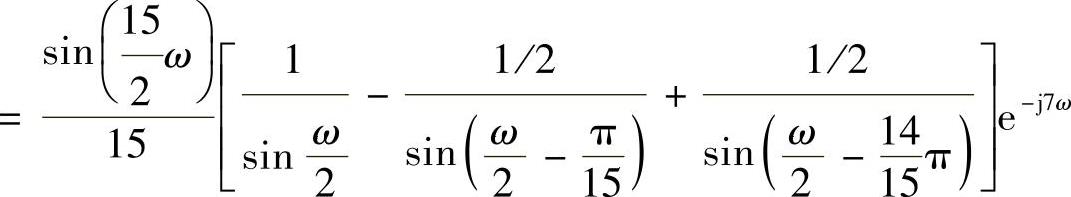
【例6.4.2】 利用频率抽样法，设计一个线性相位低通有限冲激响应数字滤波器，其理想频率特性是矩形的，已知ω_c=0.5π，抽样点数N=33为奇数。试求各抽样点的幅值Hk及相位θ_k，也即求抽样值H[k]。（理想低通滤波器的频率特性）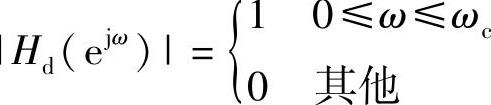

解 由N=33且低通滤波器幅频特性H（0）=1可知，这属于第一类线性相位滤波器。第一类线性相位滤波器的幅频特性H（ω）关于ω=π为偶对称，即

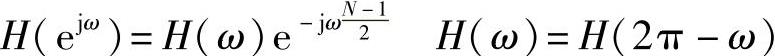
或 H[k]=H_ke^jθkH_k=H_N-k

因而有

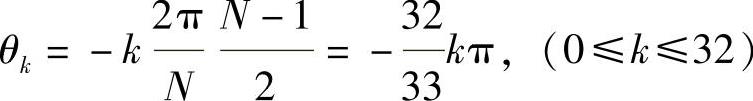
因为ω_c=0.5π，所以有

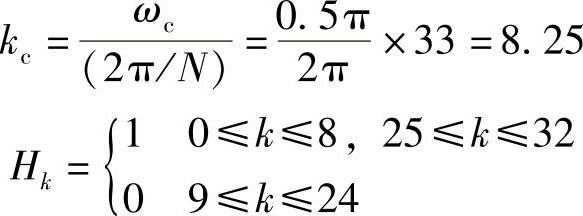
滤波器频率响应为

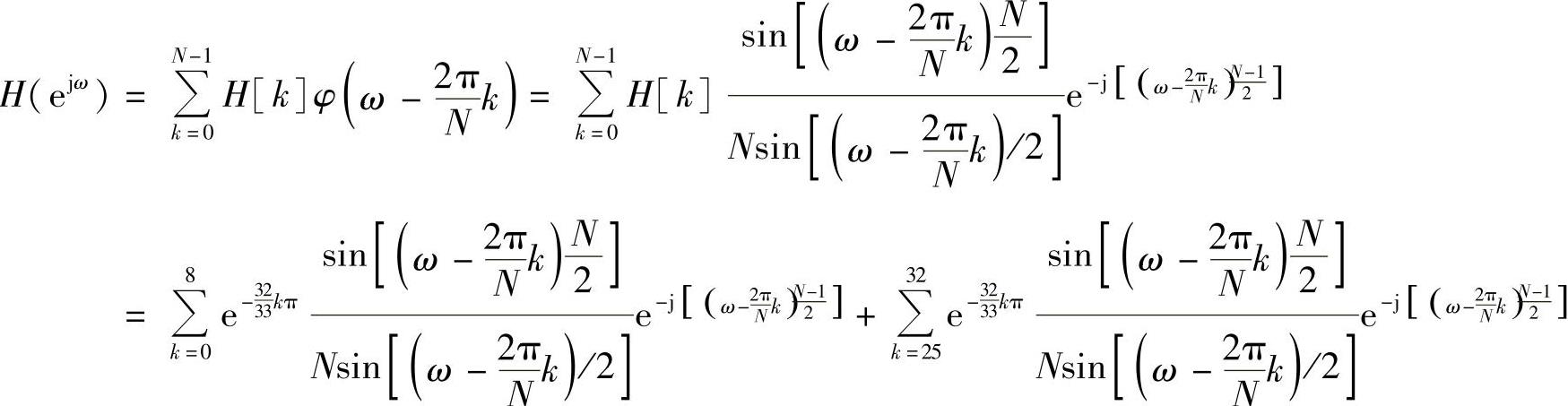
1）低通滤波器设计（ω_c=0.5π），过渡带无样本（N=33），阻带衰减为16.13dB，如图6.4.3a所示。

2）低通滤波器设计（ω_c=0.5π），过渡带1个样本（N=33），H[9]=0.5，阻带衰减为29dB，如图6.4.3b所示。

3）低通滤波器设计（ω_c=0.5π），过渡带1个样本（N=33），H[9]=0.3904（优化），阻带衰减为42.1dB，如图6.4.3c所示。

4）低通滤波器（ω_c=0.5π），过渡带2个样本（N=33），H[9]=0.5886，H[10]=0.1065（优化），阻带衰减为66.1dB，如图6.4.3d所示。

5）低通滤波器（ω_c=0.5π），过渡带2个样本（N=65），H[9]=0.5886，H[10]=0.1065（优化），阻带衰减为66.1dB，与4）相比，过渡带变窄，如图6.4.3e所示。

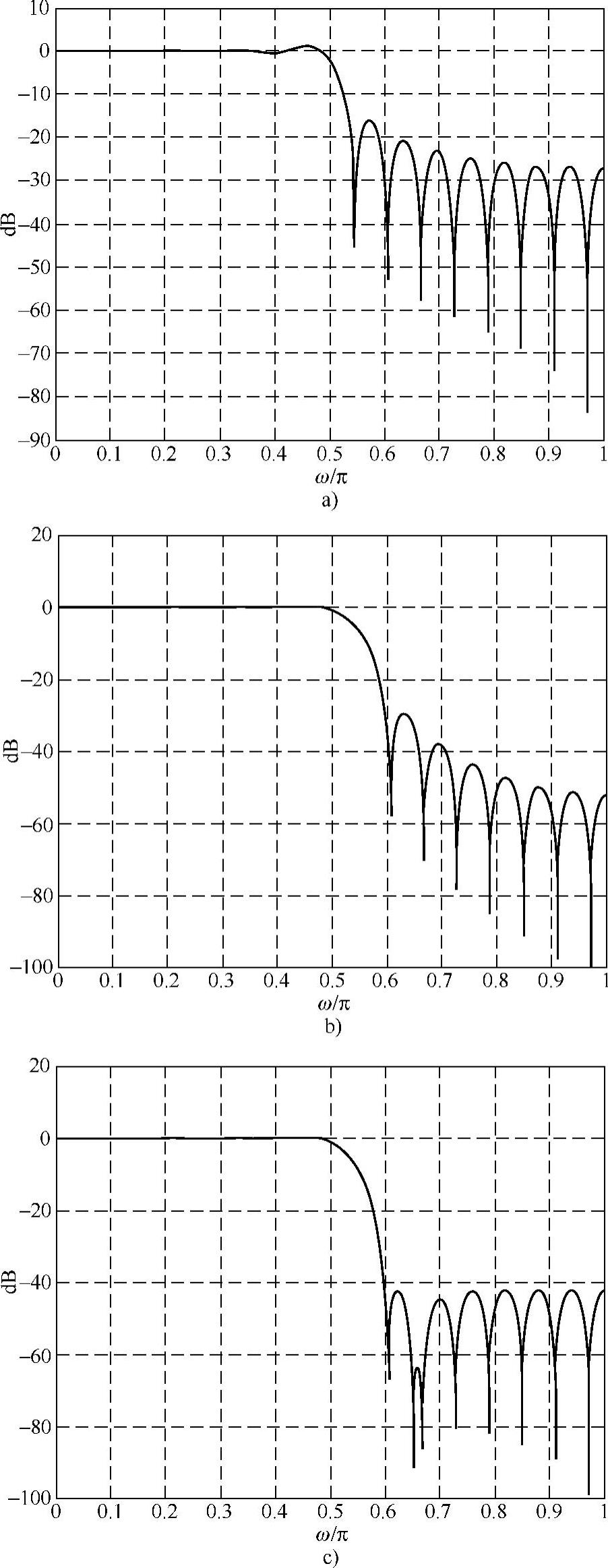
图6.4.3 例6.4.2图

a）例6.4.2中过渡带无样本 b）例6.4.2中过渡带1个样本H[9]=0.9 c）例6.4.2中过渡带1个样本H[9]=0.3904

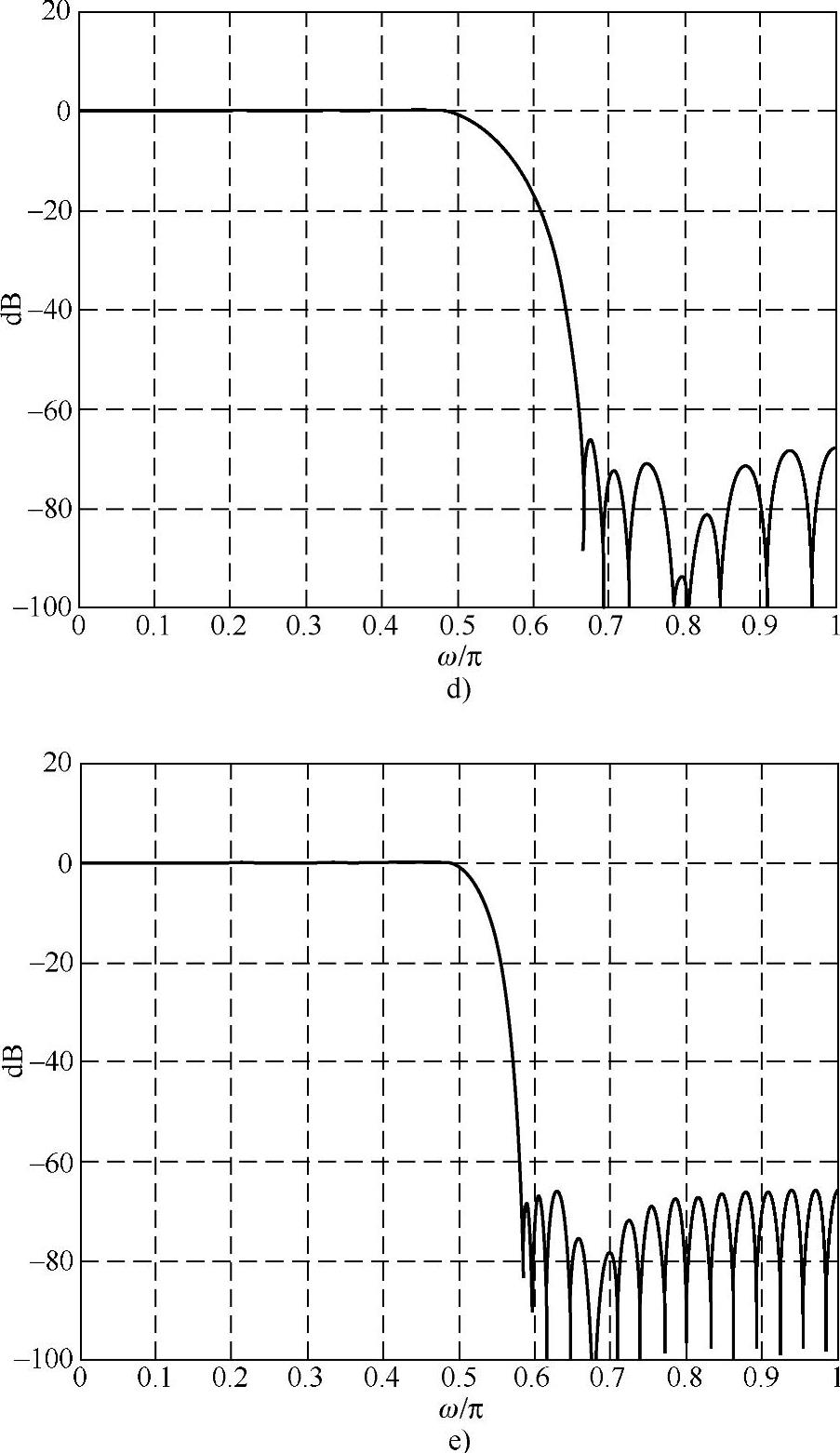
图6.4.3 例6.4.2图（续）

d）例6.4.2中过渡带2个样本N=33，H[9]=0.3904，H[10]=0.1065 e）例6.4.2中过渡带2个样本N=65，H[9]=0.3904，H[10]=0.1065