有效设计原理：梯形 vs 矩形频率响应

窗函数法是从时域出发，把希望的h_d[n]用一定形状的窗函数截取成有限长的h[n]，设计出有限冲激响应数字滤波器，这样得到的频率响应逼近于要求的理想滤波器的频率响应。

而频率抽样法则是从频域出发，由希望的滤波器频率响应H_d（e^jω）的频率抽样值H_d[k]来设计有限冲激响应滤波器，并按此离散傅里叶变换H_d[k]来唯一确定有限长序列h[n]。

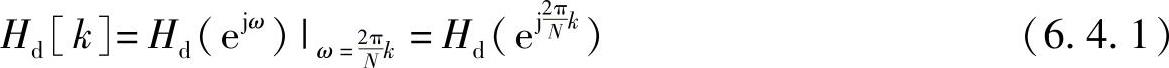
如果已知h[n]或给定的h_d[n]，则需根据z变换公式求出H_d（z）。当由于某种原因直接给出H_d（z）时，可令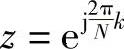求出H[k]，即

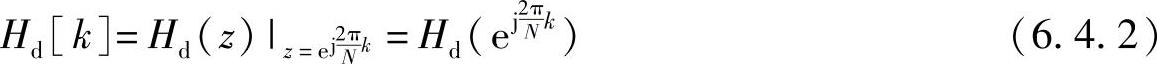
然后，以H_d[k]的N个值作为实际有限冲激响应数字滤波器频率响应H[k]，即令

H[k]=H_d[k] （0≤k≤N-1）

对H[k]作逆离散傅里叶变换可唯一确定有限长序列h[n]，即

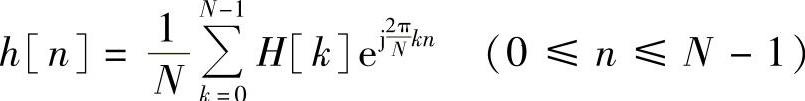
以上就是频率抽样法设计有限冲激响应数字滤波器的基本原理。此外，由频域内插公式知道，利用这N个频域抽样值H[k]同样可求得有限冲激响应数字滤波器的系统函数H（z），即

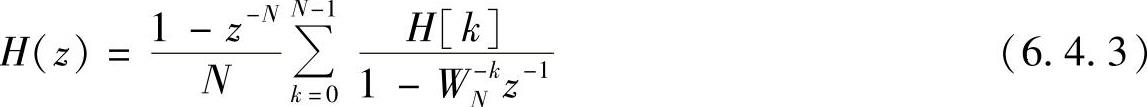(www.xing528.com)

及其频率响应

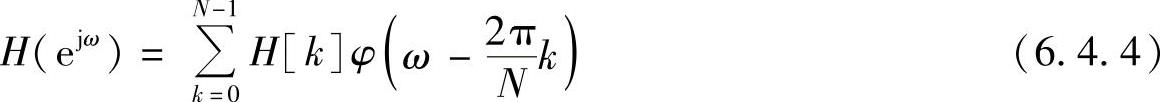
式中，φ（ω）是内插函数

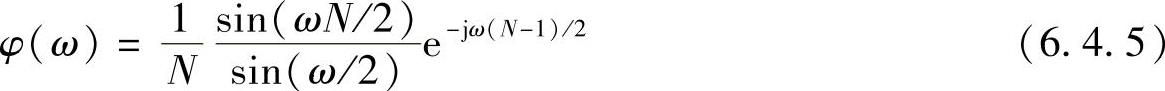
由式（6.4.4）、式（6.4.5）可见，在各个抽样频率点，实际滤波器的频率响应与希望滤波器频率响应的数值严格相等，逼近误差将为零。而在各抽样频率点之间，频率响应则是由各抽样点的加权内插函数的加权叠加形成的，因而存在一定的逼近误差。逼近误差为有限值，误差大小则取决于希望频率响应的曲线形状和抽样点的密度。

希望频率响应变化越平缓，内插值越接近希望值，逼近误差越小。反之，如果抽样点之间的希望频率特性变化越迅速，则内插值与希望值的误差就越大。因此，在希望频率特性的不连续点附近会形成振荡特性。抽样点数越多，即抽样频率越高，误差越小。图6.4.1示出了此结果。图中细线为理想频率响应H_d（e^jω），圆点表示其抽样值H[k]，粗线表示H[k]的连续内插，即H（e^jω）。图6.4.1b为理想的梯形频率响应，变化较缓慢，H（e^jω）对H_d（e^jω）逼近较好。图6.4.1a为一理想矩形频率响应，在通带和阻带之间不连续，变化剧烈，H（e^jω）对H_d（e^jω）逼近得较差，出现的肩峰和起伏比图6.4.1b大。

可见抽样点上滤波器的频率响应严格地和理想频率响应相等，抽样点之间的频率响应则是由各抽样点的加权内插函数的延伸叠加而成的，有逼近误差，误差大小取决于理想频率响应形状。理想频率响应特性变化越平缓，则内插值越接近理想值，逼近误差越小。抽样点之间的理想频率特性变化越陡，则内插值与理想值的误差就越大，在理想频率特性的不连续点附近，就会产生肩峰和起伏。

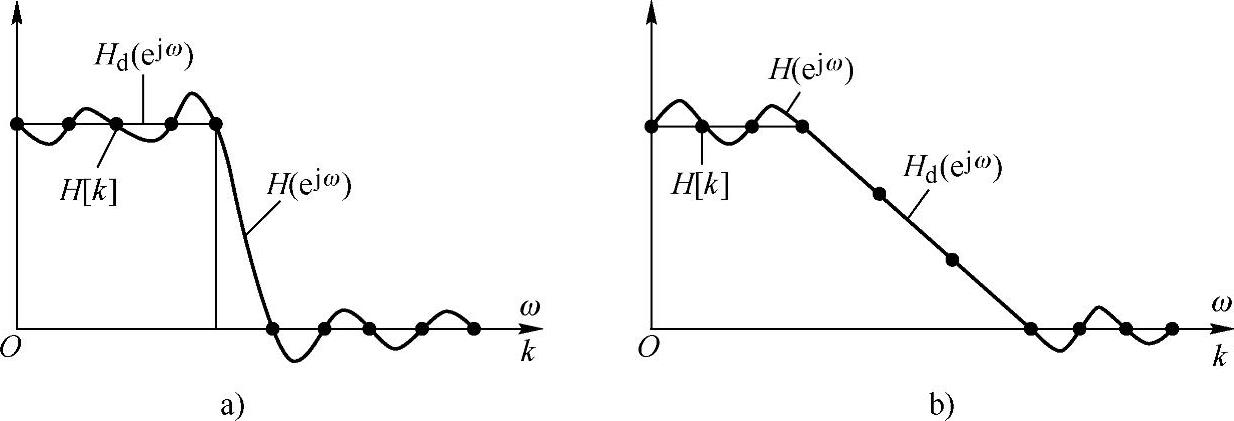
图6.4.1 逼近误差