使用窗函数法设计数字滤波器步骤及验证结果

综上所述，窗函数法设计有限冲激响应数字滤波器的过程如下：

1）根据给定的阻带衰减选定合适的窗函数w[n]类型。原则是在保证阻带衰减满足要求的情况下，尽量选择主瓣窄的窗函数。

2）根据所选窗函数和给定的过渡带宽求出窗函数的长度N值。

设待求滤波器的过渡带用Δω表示，它近似等于窗函数主瓣宽度。由表6.3.1～表6.3.3查表可得各种窗函数下的过渡带Δω计算公式与要求的过渡带宽计算N。

由表可见，过渡带宽近似与窗函数长度成反比，因此，要保证过渡带宽要求的话，所取的N值应大于计算的N值。

此外，N的取值还取决于滤波器的性质，如设计高通滤波器，N不能取偶数等。

3）由给定的指标确定希望逼近的频率响应函数H_d（ω），包括幅频特性和相频特性。如要求滤波器相频特性是线性的，应满足相应的条件。

4）根据给定的H_d（e^jω）求出h_d[n]。

①如果H_d（e^jω）的形式较简单，可以通过解析法计算

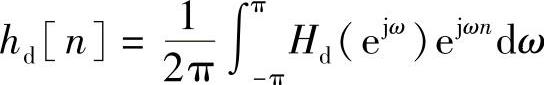
②如果H_d（e^jω）很复杂或不能直接计算积分，则必须用求和代替积分，以便在计算机上计算，也就是要通过计算离散傅里叶变换来计算。

也就是说，首先要将H_d（e^jω）抽样，抽样点数M，得到抽样值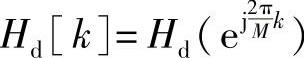，然后计算H_d[k]的M点离散傅里叶逆变换即可。由于H_d（e^jω）通常都是分段常数型（例如低通滤波器）的，那么，h_d[n]一般是无限长的序列。因此，选择有限的M值对H_d（e^jω）抽样是不满足频域抽样定理的，也就是说，由有限点的H_d[k]通过离散傅里叶逆变换得到的h_M[n]是不等于h_d[n]的。必须当M→∞时，h_M[n]才能等于h_d[n]而不产生混叠现象，即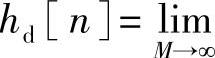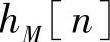。实际上，由于h_d[n]随n的增加衰减很快，一般只要M足够大，即M＞＞N，近似就足够了。

5）计算所设计的有限冲激响应数字滤波器的单位抽样响应h[n]=h_d[n]w[n]。

6）验证设计结果，即计算出H（e^jω）或H（ω），核对是否合乎给定的指标。若不满足设计指标，重复2）～4）步，进行修正设计，直到满足设计指标为止。

7）由h[n]求有限冲激响应数字滤波器的系统函数。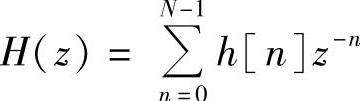

8）根据系统函数实现有限冲激响应滤波器。

【例6.3.1】 用矩形窗、汉宁窗、海明窗、布莱克曼窗设计线性相位有限冲激响应低通数字滤波器，其中，N=21，ω_c=0.2π。

解 1）根据题意，低通滤波器的频率特性为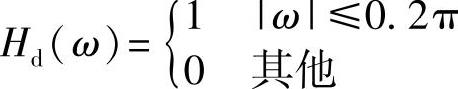；相频特性为θ（ω）=-ω（N-1）/2=-10ω。

2）求出h_d[n]，即

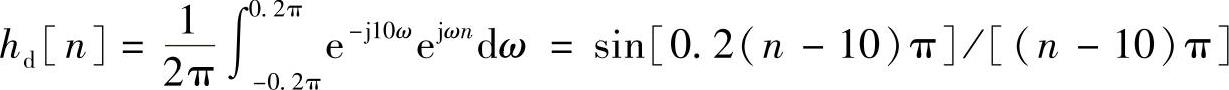
3）加窗，得h[n]=h_d[n]w[n]。

4）加不同窗下的滤波器的频率特性。

①加矩形窗，如图6.3.5所示。

②加汉宁窗，如图6.3.6所示。

③加海明窗，如图6.3.7所示。

④加布莱克曼窗，如图6.3.8所示。

【例6.3.2】 设计一个线性相位有限冲激响应低通数字滤波器，给定抽样频率为f_s=15kHz，通带截止频率为f_p=1.5kHz，阻带截止频率为f_st=3kHz，阻带衰减不小于50dB。(www.xing528.com)

解 1）求数字频率为

ω_p=f_p/f_s×2π=1.5/15×2π=0.2π

ω_st=f_st/f_s×2π=3/15×2π=0.4π

过渡带宽为Δω=ω_st-ω_p=0.2π；

中心频率为ω₀=（ω_st+ω_p）/2=0.3π。

2）由阻带衰减50dB查表，可选海明窗，（衰减53dB）。

3）由过渡带求N为

Δω=8π/N≤0.2π ⇒ N≥40

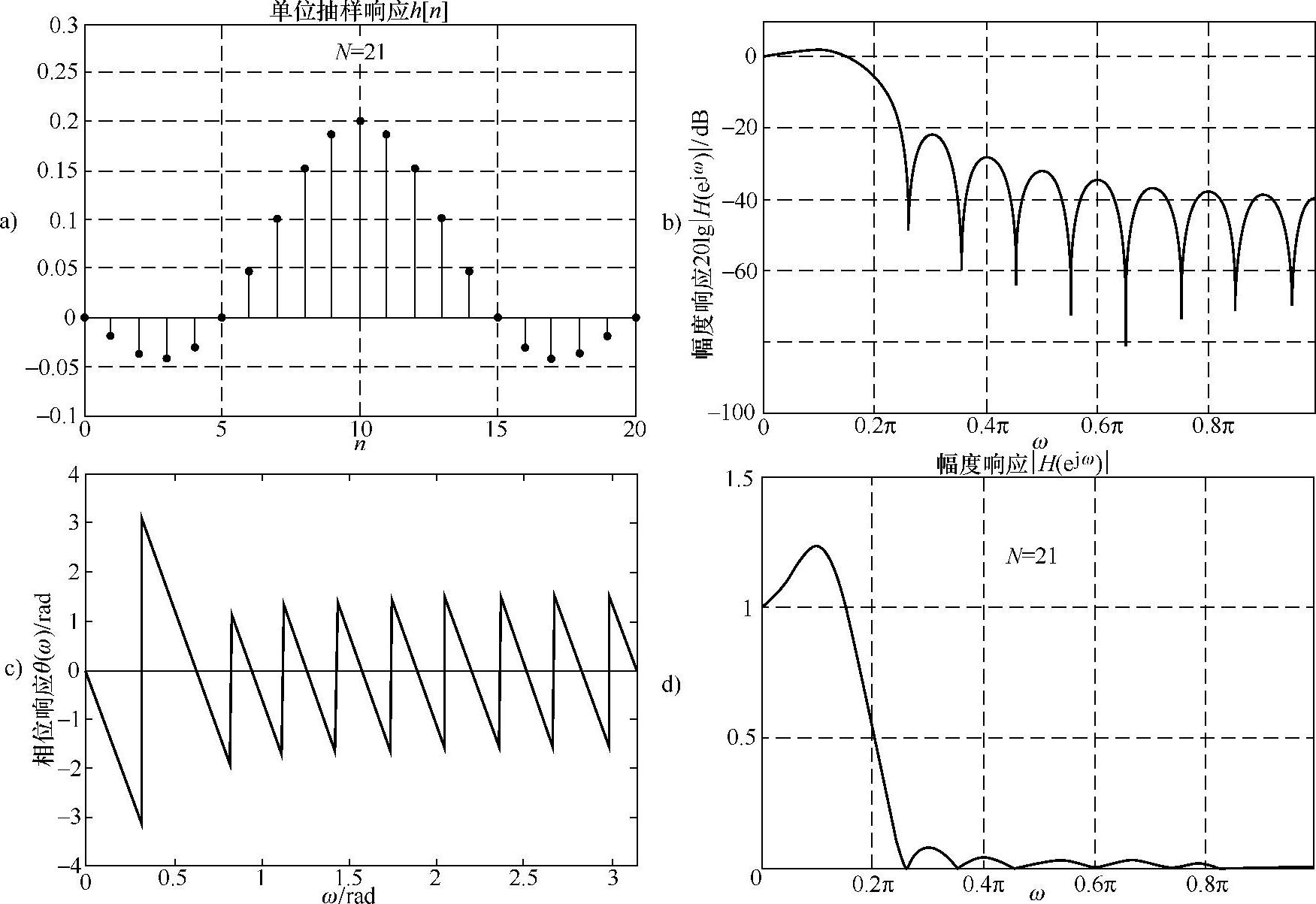
图6.3.5 加矩形窗的频率特性

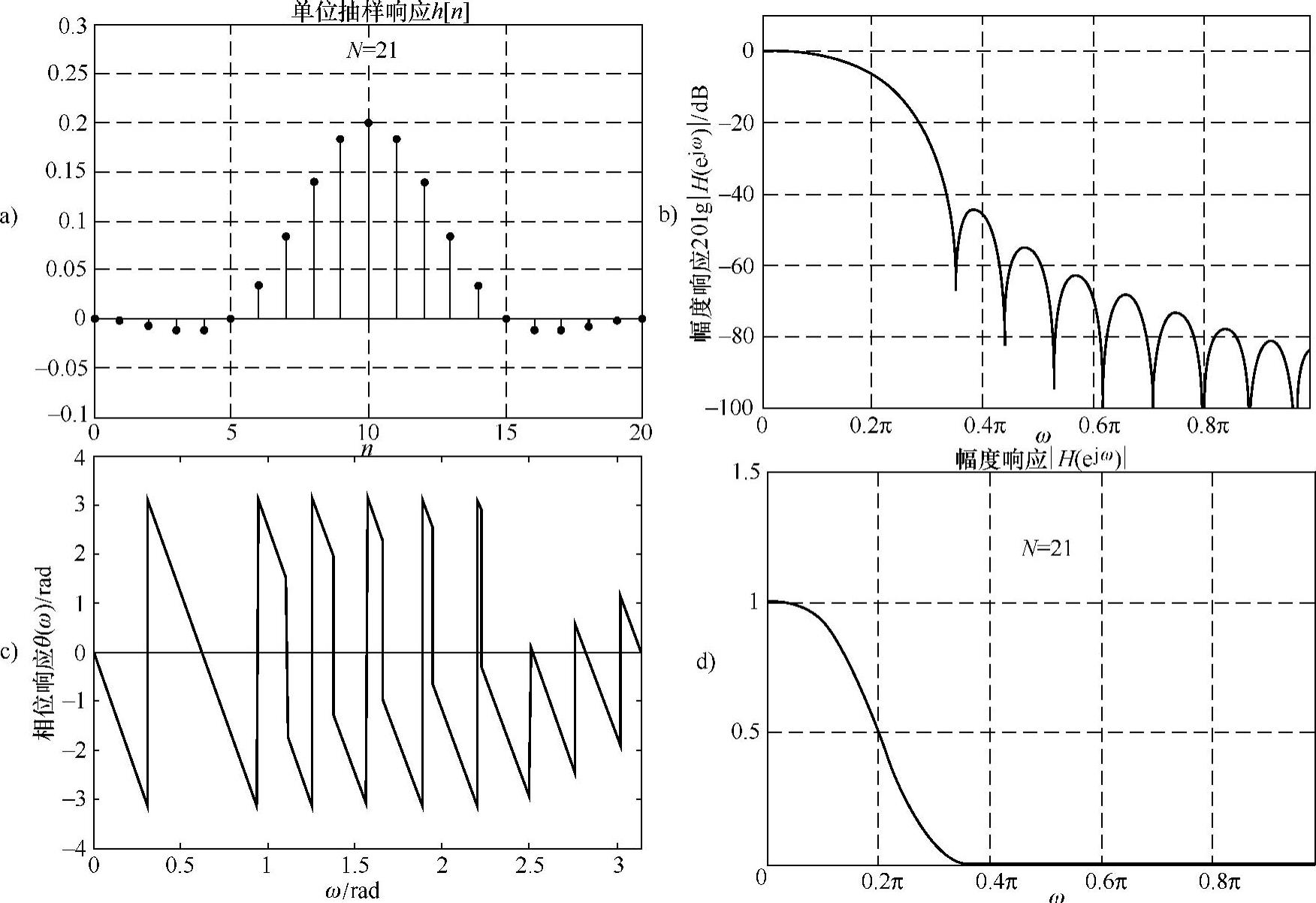
图6.3.6 加汉宁窗的频率特性

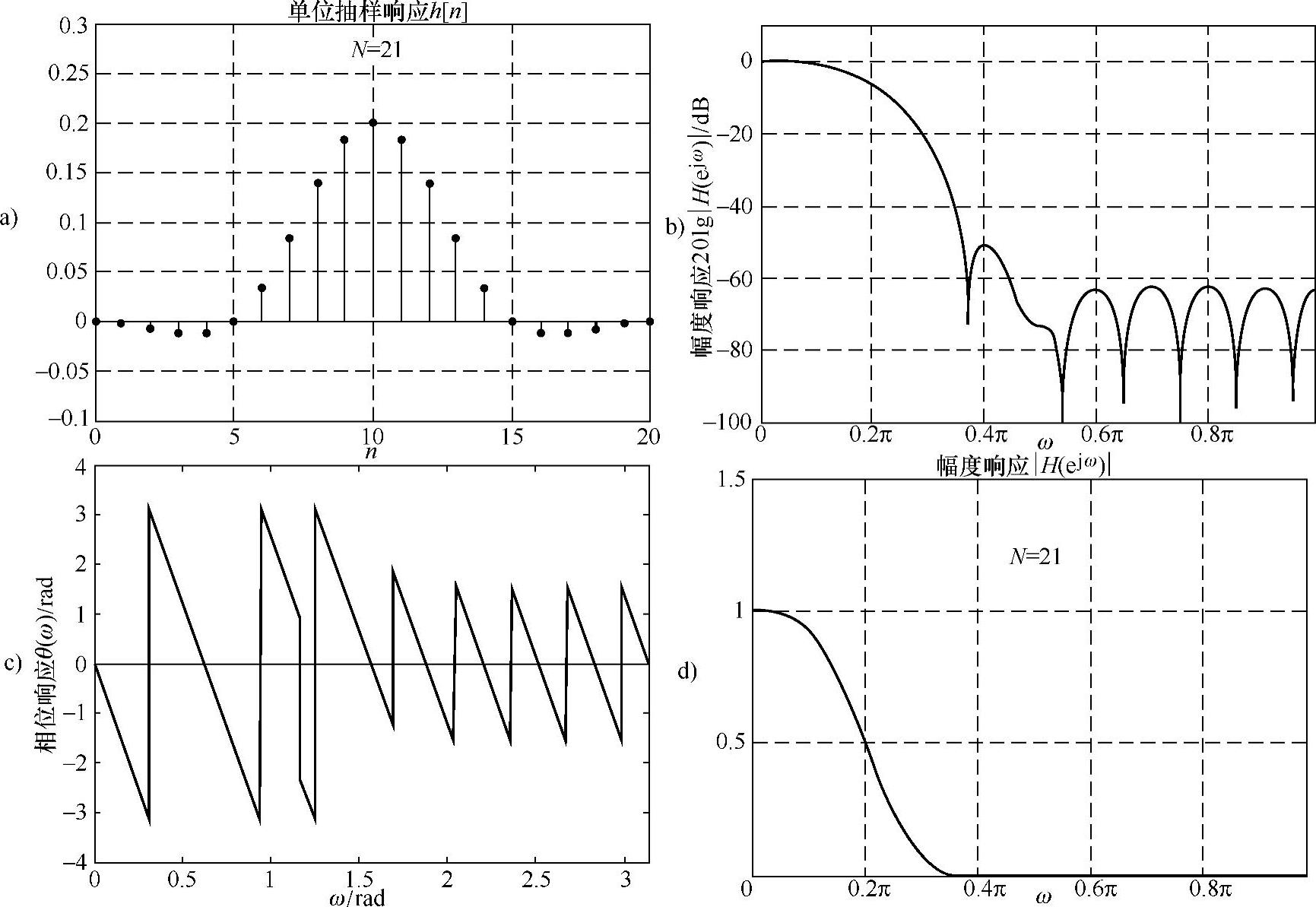
图6.3.7 加海明窗的频率特性

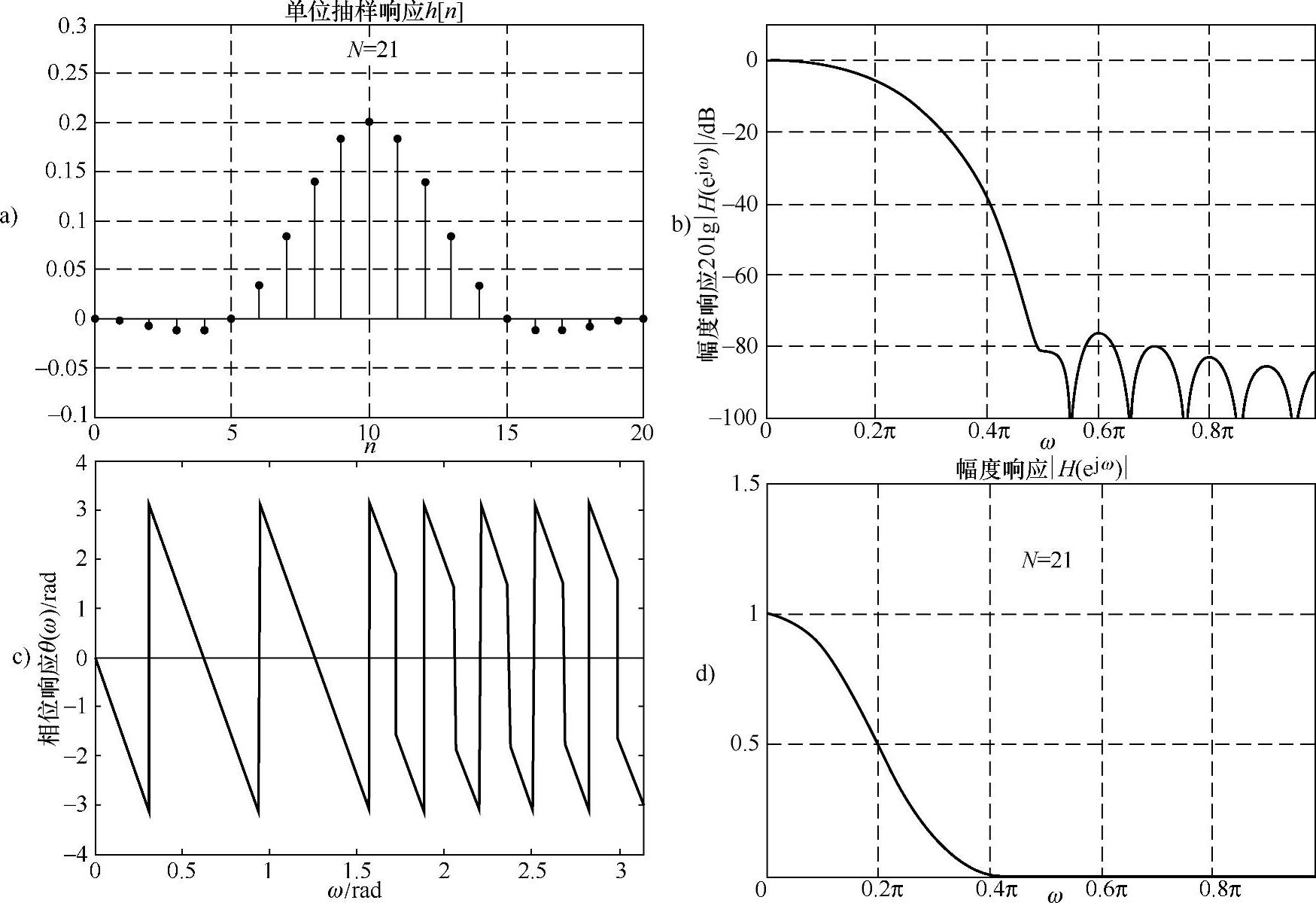
图6.3.8 加布莱克曼窗的频率特性

取N=40。

4）依据题意，得理想低通滤波器

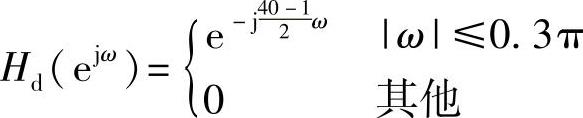
5）计算h_d[n]得

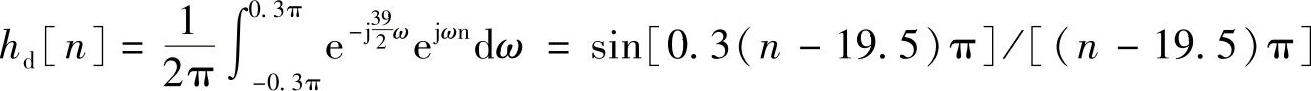
6）加窗，得h[n]=h_d[n]w[n]。

7）求H（e^jω），验证。实际阻带衰减为53dB，均满足设计指标要求。

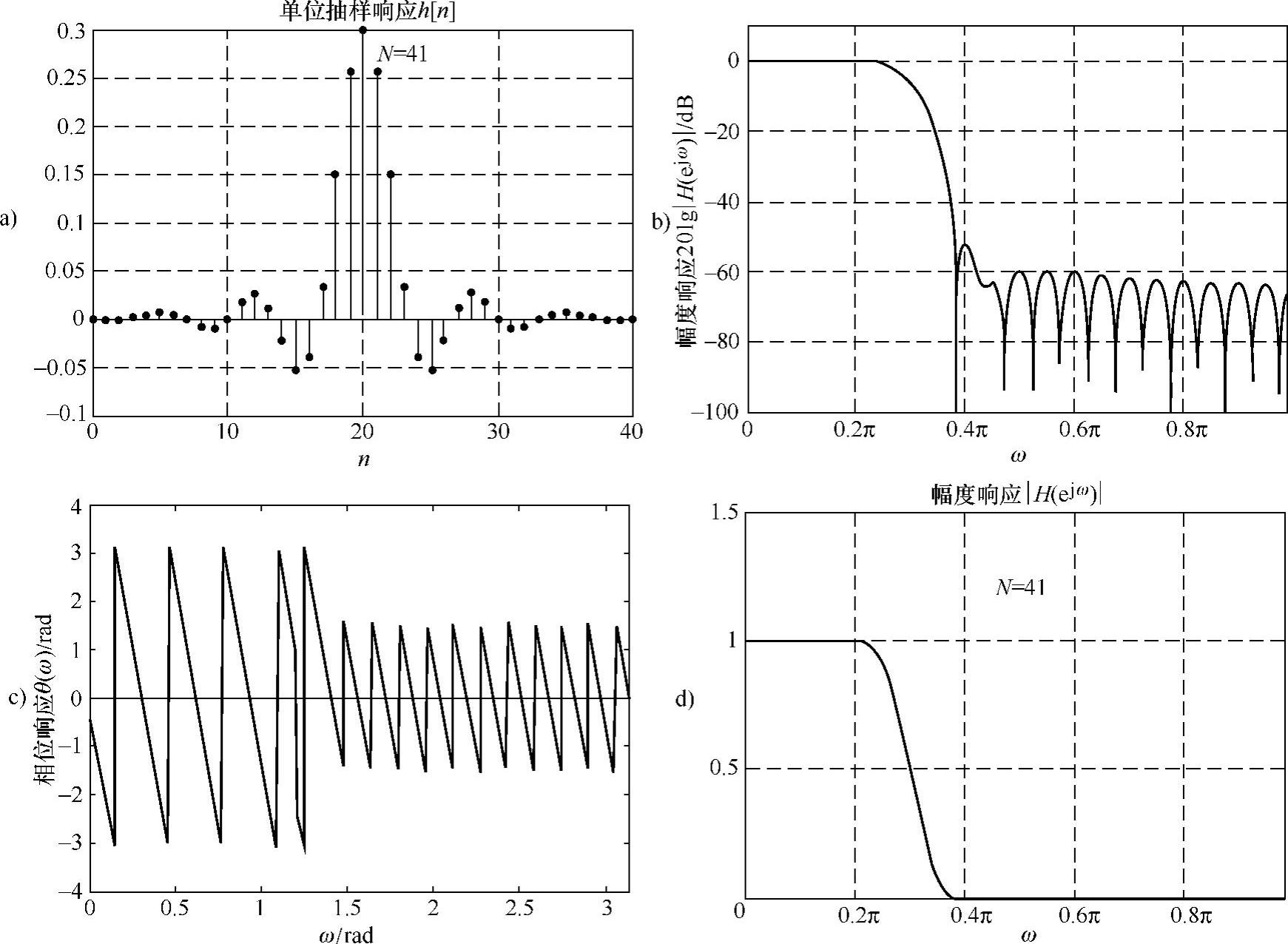
图6.3.9 例6.3.2的频率特性

窗函数法特点：窗函数法设计的主要优点是简单，使用方便。窗函数大多有封闭的公式可循，性能、参数都已有表格、资料可供参考，计算程序简便，所以很实用；缺点是通带和阻带的截止频率不易控制。