常用的六种窗函数及其特点

由上节讨论可见，矩形窗截断造成的肩峰值为8.95%，则阻带最小衰减为20lg（8.95%）=-21dB，这个衰减量在工程上常常是不够大的。

为了加大阻带衰减，只能改变窗函数的形状。只有当窗谱逼近冲激函数时，也就是绝大部分能量集中于频谱中点时，H（ω）才会逼近H_d（ω）。这相当于窗的宽度为无限长，等于不加窗口截断，这没有实际意义。

从以上讨论中看出，窗函数序列的形状及长度的选择很关键，一般希望窗函数满足两项要求：

1）窗谱主瓣尽可能地窄，以获取较陡的过渡带。

2）尽量减少窗谱的最大旁瓣的相对幅度。也就是能量尽量集中于主瓣，这样使肩峰和波纹减小，就可增大阻带的衰减。

但是，在实际设计中，在N一定时，这两项要求是不能同时都满足的：当选用主瓣宽度较窄时，虽然得到较陡的过渡带，但通带和阻带的波动明显增加；当选用小的旁瓣时，会使主瓣宽度增加，虽能得到平坦的幅频特性和较小的阻带波纹，但过渡带加宽。

因此，实际所选用的窗函数往往是它们的折中。常以增加主瓣宽度来换取相对旁瓣的抑制。同时，为不使过渡带边宽，可用增加N的方法使主瓣变窄。

以上是从幅频特性的改善对窗函数提出的要求。实际上设计的有限冲激响应数字滤波器往往要求具有线性相位。

设计有限冲激响应数字滤波器时，首先根据阻带衰减的要求选择合适的窗函数序列（由表6.3.1和6.3.2查得），确定窗函数后，便可知其主瓣宽度，根据给定的过渡带宽，可确定窗函数宽度N。下面介绍常用的三类窗族。

1.布莱克曼（Blackman）窗族

这类窗族的一般表示式为

对应各种窗函数的K值和系数见表6.3.1。

表6.3.1 布莱克曼窗族的各项指标

1）汉宁（Hanning）窗，K=1，a₀=a₁=0.5，又称升余弦窗，其表达式和其幅度谱为

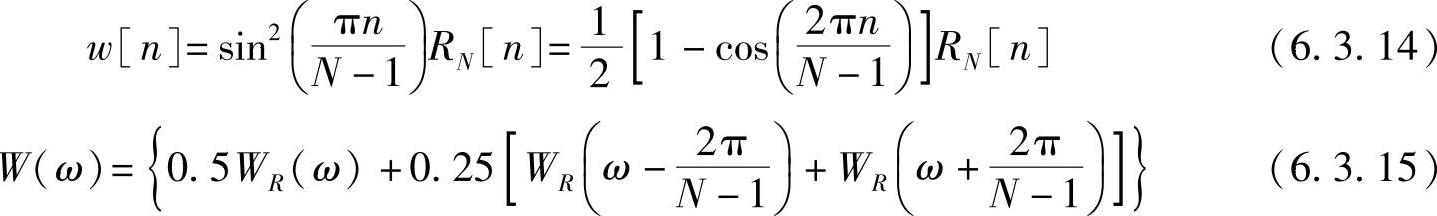
这三部分之和，使旁瓣互相抵消，能量更集中在主瓣，它的最大旁瓣值比主瓣值约低31dB。但是代价是主瓣宽度比矩形窗的主瓣宽度增加一倍，即为8π/N。

2）海明（Hamming）窗，K=1，a₀=0.54，a₁=0.46，又称改进的升余弦窗，其表达式及其幅度谱分别为

与汉宁窗相比，两者主瓣宽度相同，为8π/N，但旁瓣又被进一步压低，结果可将99.963%的能量集中在窗谱的主瓣内，它的最大旁瓣值比主瓣值约低41dB。

3）布莱克曼（Blackman）窗，K=2，a₀=0.42，a₁=0.5，a₂=0.08，又称二阶升余弦窗，其表达式及其幅度谱分别为

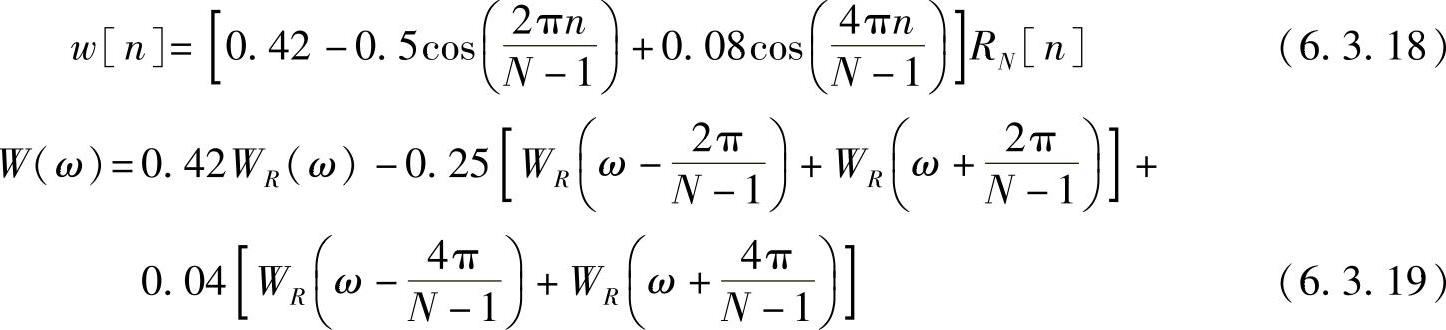
最大旁瓣值比主瓣值约低57dB，但是主瓣宽度是矩形窗的主瓣宽度的3倍，即为12π/N。

2.三角（Bartlett）窗

此种窗的数学表达式及其幅度谱分别为(www.xing528.com)

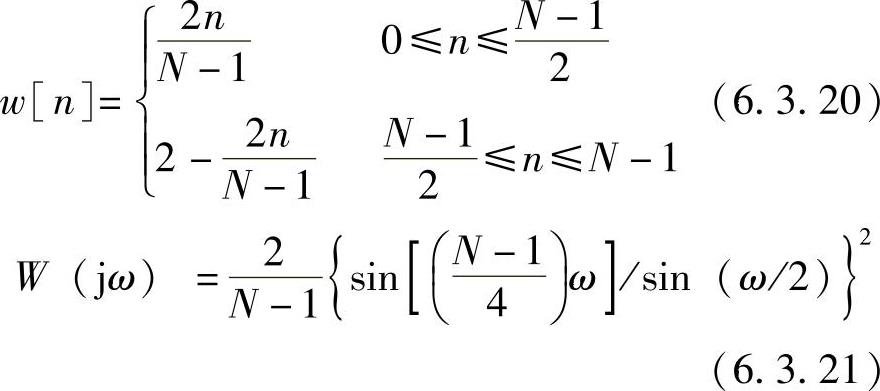
此时，主瓣宽度为8π/N，比矩形窗主瓣宽度增加一倍，但旁瓣却小很多，最大旁瓣电平为-25dB。

图6.3.3绘出了上述窗函数的图形（包络），图6.3.4绘出了各窗函数的频谱幅度。

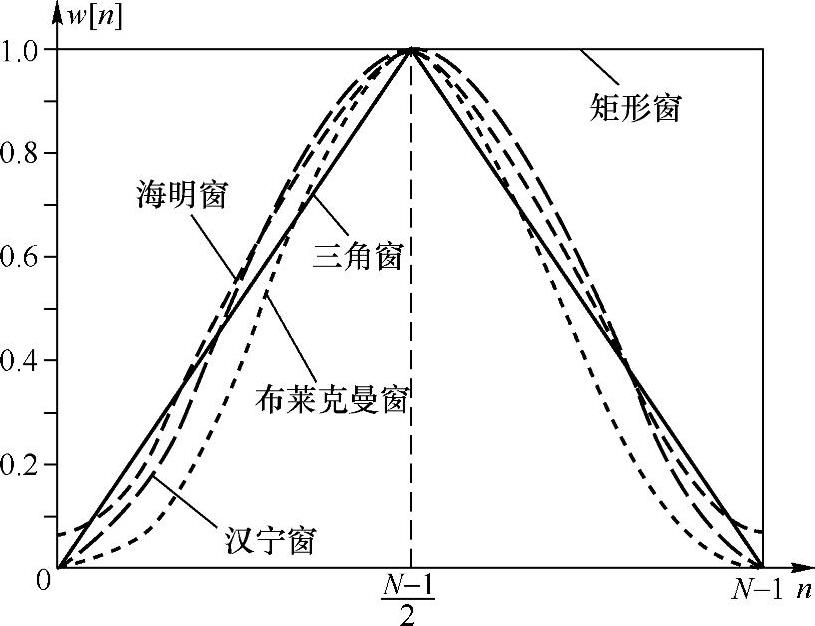
图6.3.3 五种常用的窗函数的图形

3.凯塞（Kaiser）窗族

此类窗族的特点是适应性强，其表达式为

式中，β是一个可自由选择的参数。通常情况下，β=4～9，β值增大，则其频谱旁瓣降低，主瓣增宽。I₀（x）是第一类修正零阶贝塞尔函数，可用下面级数表示，即

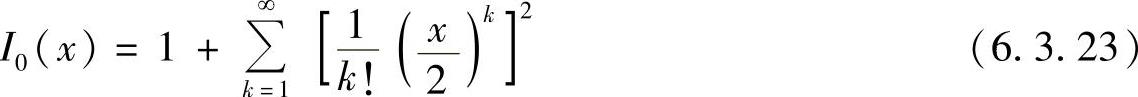
这个无穷级数，可用有限项级数去近似，项数多少由要求的精度来确定。因而采用计算机是很容易求解的。

凯塞窗族频谱的幅频函数为

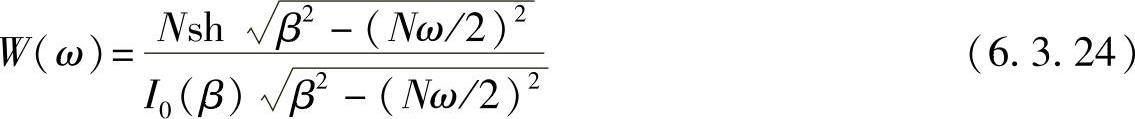
表6.3.2列出了不同β值凯塞窗族W（ω）的旁瓣电平（以dB表示）、阻带衰减和过渡带宽Δω。

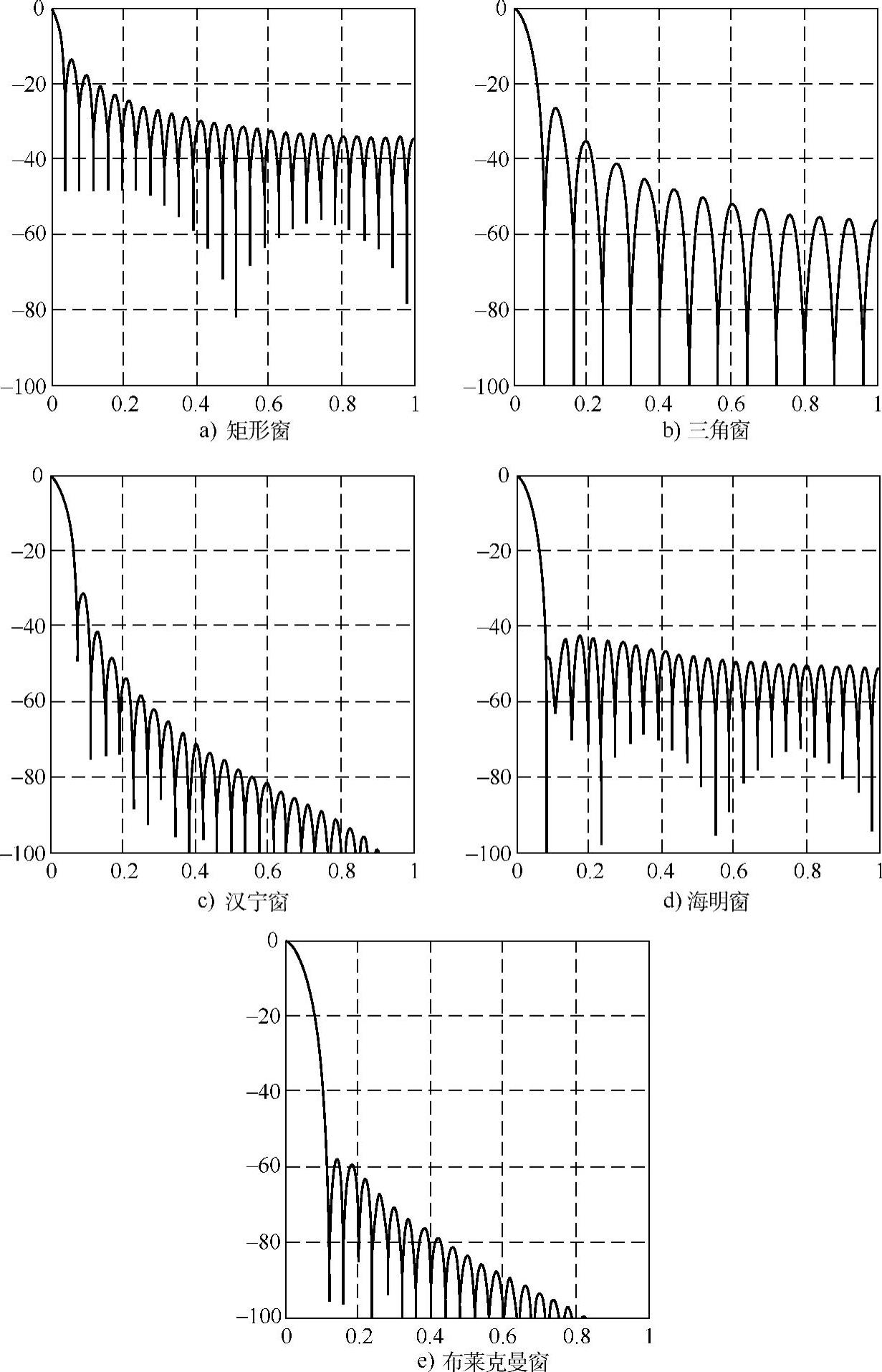
图6.3.4 各种窗函数的傅里叶变换（N=51）

注：图中横坐标是数字角频率（ω），纵坐标是幅度（A=20lgW（ω）/W（0））。

表6.3.2 凯塞窗族的性能

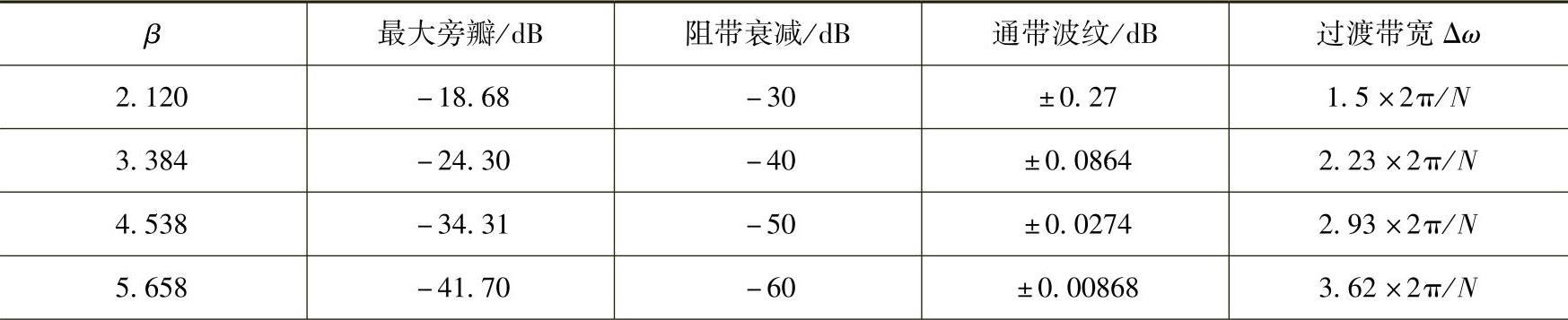
（续）

由表6.3.1和表6.3.2可见，利用窗函数法设计有限冲激响应数字滤波器，所得滤波器的阻带衰减通常比窗函数频谱的最大旁瓣衰减要大，这是由于H_d（ω）与W（ω）的卷积过程对窗函数的旁瓣起了平滑作用。一般滤波器的阻带衰减与窗函数频谱的最大旁瓣衰减相差约7～8dB以上，选用窗函数时应注意这一点。

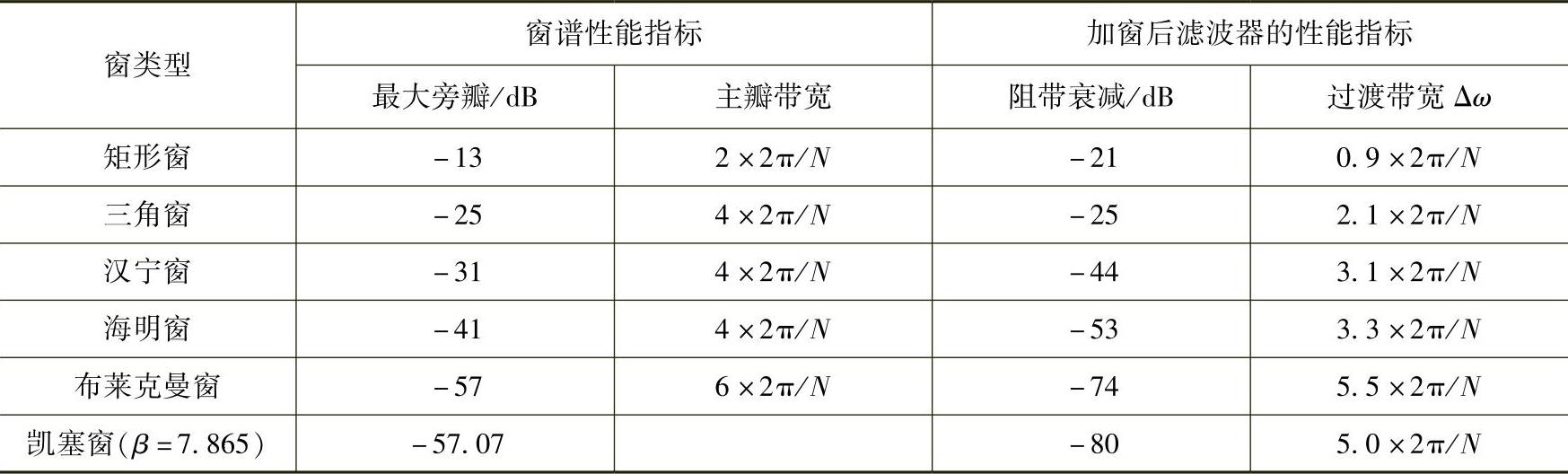
为了应用方便，表6.3.3给出了常用的六种窗函数的基本参数及性能

表6.3.3 常用的六种窗函数的基本参数及性能