如何解决Gibbs现象？

为了说明所选用的窗函数w[n]对H（e^jω）逼近H_d（e^jω）程度的影响，需要分析H（e^jω）与窗函数w[n]、H_d（e^jω）的关系，以便明确如何正确的选择窗函数序列w[n]。

现以一矩形窗函数来截取h_d[n]，为保证截取的h[n]偶对称，需保证其位移α满足α=（N-1）/2条件，位移并不影响H_d（e^jω）的幅频函数H_d（ω），只影响其相频函数。根据卷积定理，时域乘积相当于频域卷积，即h[n]=h_d[n]w[n]的傅里叶变换为

式中

式中，α=（N-1）/2，则

W_R（ω）=sin（Nω/2）/sin（ω/2）（6.3.7）幅频函数W_R（ω）是周期的偶对称函数，在-2π/N≤ω≤2π/N范围内形成主瓣，主瓣宽度为4π/N，两侧形成许多衰减振荡的旁瓣，如图6.3.1所示。通常主瓣定义为原点两边第一个过零点之间的区域。

图6.3.1 矩形窗的频谱

若将理想滤波器的频率响应也写成

H_d（e^jω）=H_d（ω）e^jωα （6.3.8）

式中，H_d（ω）为滤波器的幅频特性。

将W_R（e^jω）和H_d（e^jω）代入式（6.3.5）得

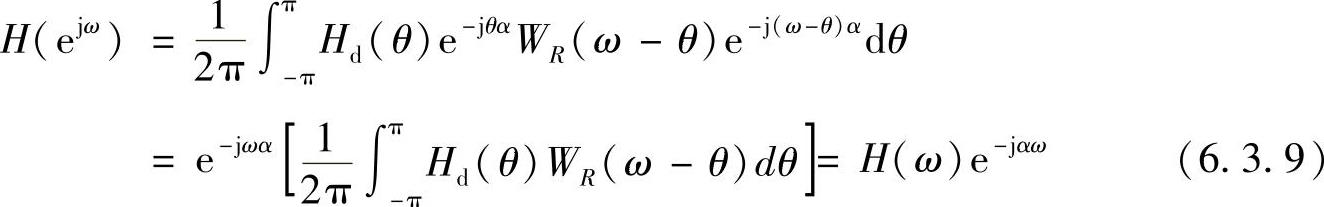
可见相频函数θ（ω）=-αω是线性的，幅频函数H（ω）为H_d（ω）与W_R（ω）的卷积。

当H_d（ω）为

(www.xing528.com)

时，对实际有限冲激响应数字滤波器的幅频特性H（ω）有影响的只是窗函数的幅频特性W_R（ω）。实际有限冲激响应数字滤波器的幅频特性是理想低通滤波器的幅频特性与窗函数的幅频特性的卷积。

H_d（ω）和W_R（ω）的卷积过程如图6.3.2所示。由图6.3.2可以看出，卷积所得的H（ω）有起伏波纹。

图6.3.2 矩形窗对理想低通幅频特性的影响

1）ω=0时，，为图6.3.2a、c两函数乘积的积分，即等于W_R（-θ）在-ω_c≤ω≤ω_c区间的积分，通常ω_c＞＞2π/N，H（0）实际上近似等于W_R（θ）在全部积分区域内的积分（θ=-π到θ=π）。

2）当ω=ω_c时，。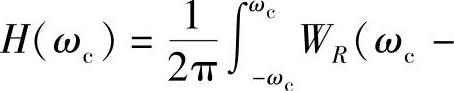

3）当ω=ω_c-2π/N时，W_R（ω-θ）的全部主瓣都在H_d（θ）的通带（|ω|≤ω_c）之内，如图6.3.2d所示。因此卷积结果有最大值，即H（ω_c-2π/N）为最大值，频率响应H（ω）=H（ω_c-2π/N）达到最大正肩峰值。

4）当ω=ω_c+2π/N时，W_R（ω-θ）的全部主瓣都在H_d（θ）的通带（|ω|≤ω_c）之外，如图6.3.2e所示。而通带内的旁瓣负的面积大于正的面积，因而卷积结果达到最负值，频率响应H（ω）=H（ω_c+2π/N）达到最大负肩峰值。

5）当ω＞ω_c+2π/N时，随着ω的继续增大，卷积值将随着W_R（ω-θ）的旁瓣在H_d（θ）的通带内面积的变化而变化，H（ω）将围绕着零值波动。

6）当ω＜ω_c+2π/N时，随着ω的减小，W_R（ω-θ）的右旁瓣进入H_d（θ）的通带，使得H（ω）值围绕H（0）值而波动。

7）而在正负两肩峰之间，ω_c-2π/N＜ω＜ω_c+2π/N，H（ω）则形成一过渡带，其宽度为Δω=4π/N，即等于W_R（ω）的主瓣宽度。

综上所述，加窗处理对理想频率响应产生以下几点影响（见图6.3.2f）：

1）H（ω）将H_d（ω）在截止频率处的间断点变成了连续曲线，使理想频率特性不连续点处边沿加宽，形成一个过渡带，过渡带的宽度等于窗函数的频率响应W_R（ω）的主瓣宽度Δω=4π/N，即正肩峰与负肩峰的间隔为4π/N。窗函数的主瓣越宽，过渡带也越宽。

2）在截止频率ω_c的两边即ω=ω_c±2π/N的地方，H（ω）出现最大的肩峰值，肩峰的两侧（过渡带两侧的通带和阻带内）形成起伏振荡，其振荡幅度取决于旁瓣的相对幅度，而振荡的形状和大小，则取决于窗函数序列频谱的主瓣和旁瓣的多少。

肩峰值的大小直接影响通带特性和阻带衰减，对滤波器的性能影响较大。在矩形窗情况下，最大相对肩峰值为8.95%，N增加时，2π/N减小，起伏振荡变密，最大相对肩峰值则总是8.95%，这种现象称为Gibbs效应。