线性相位条件的证明和特点

根据N的奇偶性及h[n]的对称性，分四种情况讨论。

第一种情况：当其单位抽样响应h[n]为偶对称，即h[n]=h[N-1-n]，且N为奇数时，此时其频率响应为

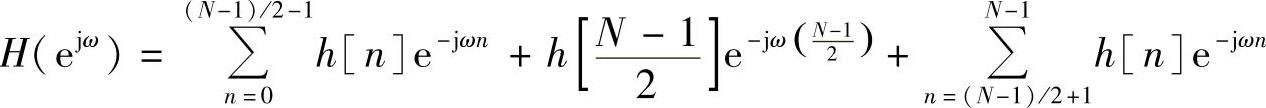
上式等号后面第三项用n=N-1-m作变量代换，得

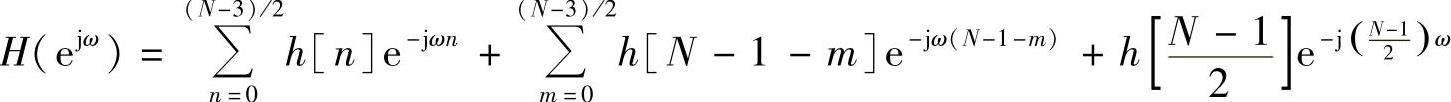
根据对称条件h[n]=h[N-1-n]，得

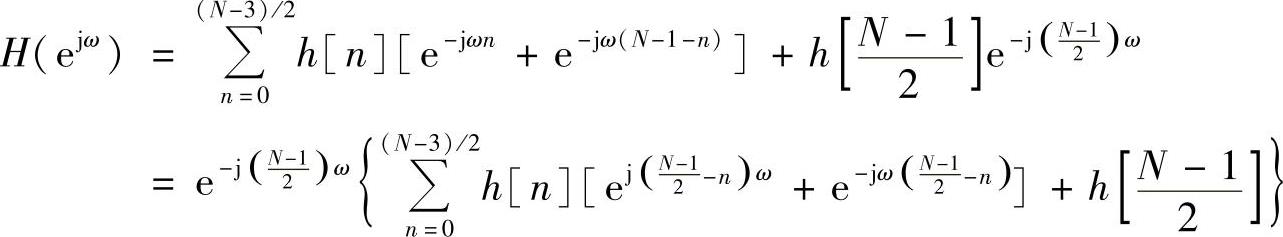
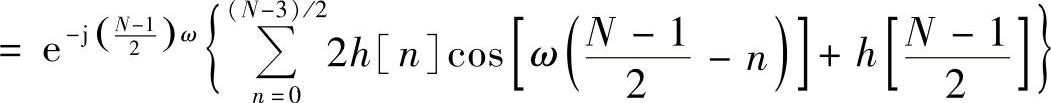
令n′=[（N-1）/2]-n代入上式，得

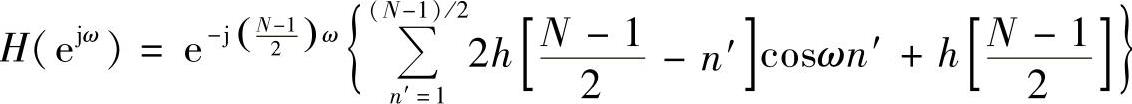
令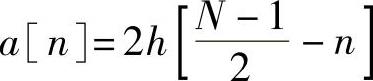，，其中n=1，2，…（N-1）/2，代入上式得

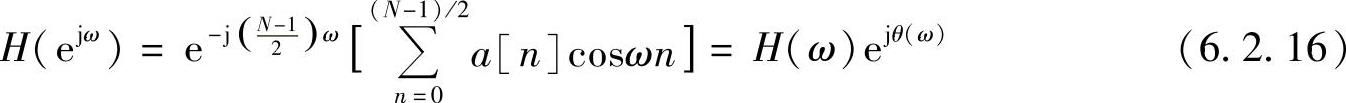
式中

称为幅频标量函数。

θ（ω）=-（N-1）ω/2 （6.2.18）

称为相频函数，显然，它是频率的线性函数。

由于式中cos（ωn）项对ω=0、π、2π皆为偶对称，因此幅频函数H（ω）对于ω=0、π、2π也呈偶对称。

第二种情况：h[n]偶对称，h[n]=h[N-1-n]，且长度N为偶数时，其频率响应为

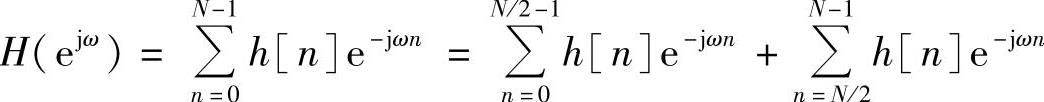
令n=N-1-m，代入上式右侧第二项，得

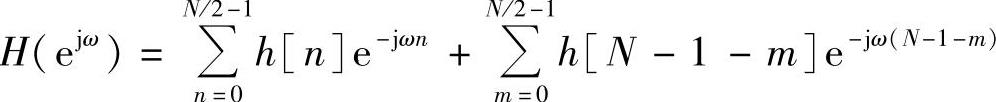
根据偶对称条件h[n]=h[N-1-n]，得

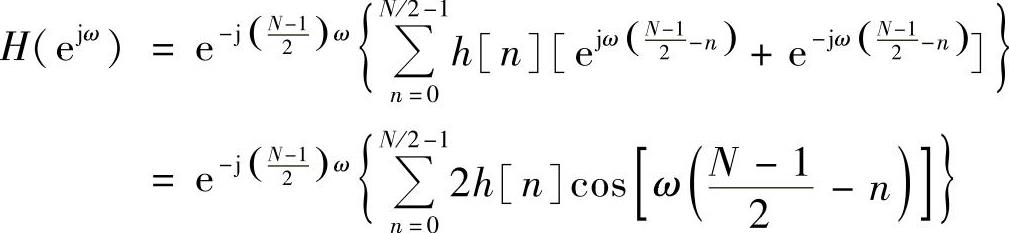
令n′=（N/2）-n，代入上式，得

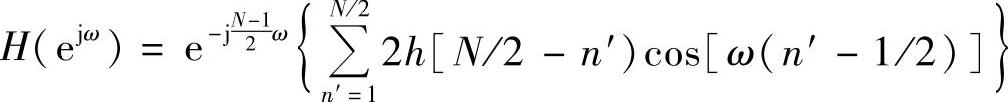
再令b[n]=2h[N/2-n]，其中n=1，2，…，N/2，则

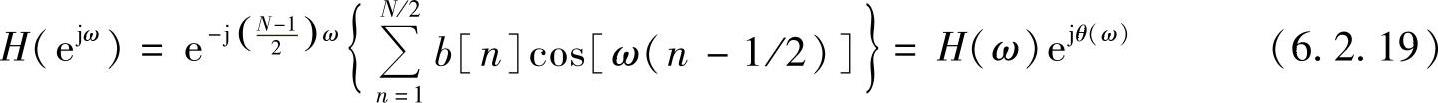
其中幅频标量函数为

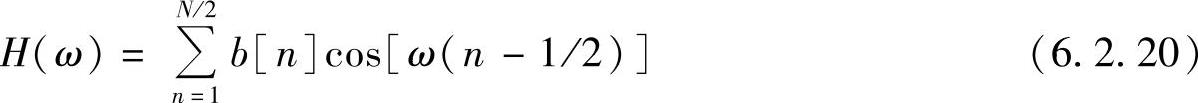
相频函数为

θ（ω）=-（N-1）ω/2 （6.2.21）

由式（6.2.21）可见，第二种情况下，滤波器也具有线性相频特性。

由式（6.2.20）可知，当ω=π时，cos[ω（n-1/2）]=0，因此H（π）=0，即H（z）在z=-1处必然有一个零点。如果数字滤波器在ω=π处不为零，例如高通滤波器、带阻滤波器，则不能用这类数字滤波器来设计。所以设计高通滤波器时，N不能取偶数。

由于余弦项cos[ω（n-1/2）]对ω=π呈奇对称，因此H（ω）关于ω=π呈奇对称。(www.xing528.com)

由于cos[ω（n-1/2）]对ω=0、2π为偶对称，故H（ω）对于ω=0、2π也呈偶对称。

第三种情况：h[n]为奇对称，h[n]=-h[N-1-n]，且N为奇数时，其频率响应为

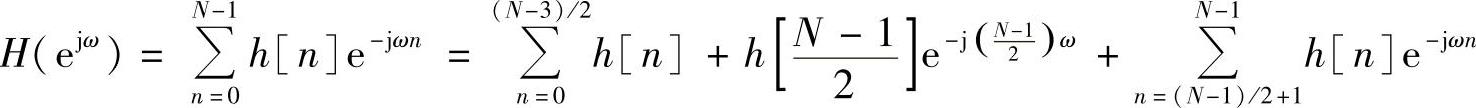
根据奇对称条件h[n]=-h[N-1-n]，得

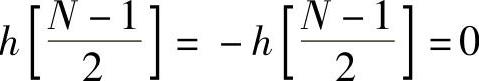
仿照第一种情况的推导过程，可得

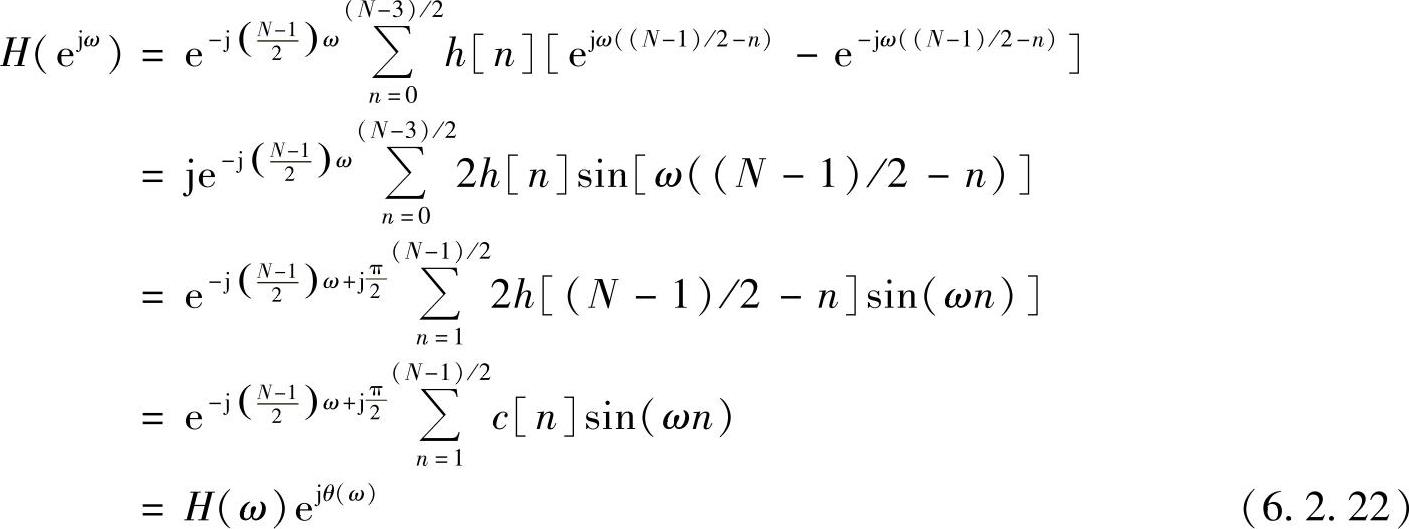
其幅度标量函数为

式中

c[n]=2h[（N-1）/2-n] （n=1，2，…，（N-1）/2） （6.2.24）

其相频函数为

θ（ω）=π/2-（N-1）ω/2 （6.2.25）

由于sin（ωn）在ω=0、π、2π处都为零，并对这些点呈奇对称，因此幅频函数H（ω）在ω=0、π、2π处为零，即H（z）在z=±1上都有零点，且H（ω）对于ω=0、π、2π也呈奇对称。因此，如果数字滤波器在ω=0、π、2π处不为零，例如低通滤波器、高通滤波器、带阻滤波器，则不能用这类数字滤波器来设计，除非不考虑这些频率点上的值。

其相频函数是ω的“准线性”函数，因它包含了相位的固定值π/2，这种情况适于做希尔伯特变换器和微分器。

第四种情况：h[n]奇对称，h[n]=-h[N-1-n]，N为偶数。仿照第二种情况的推导，得其频率响应为

H（e^jω）=H（ω）e^jθ（ω） （6.2.26）幅度标量函数为

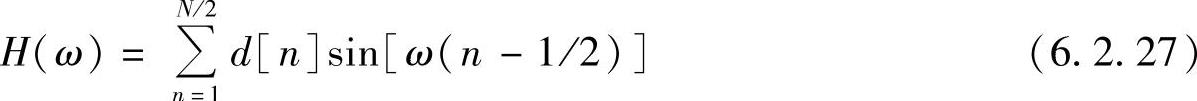
式中

d[n]=2h[N/2-n] （n=1，2，…，N/2） （6.2.28）

相频函数

θ（ω）=π/2-（N-1）ω/2 （6.2.29）

与第三种情况相同，可以看出相频函数也包含有常数项π/2。这种情况最适于设计微分器和希尔伯特变换器。

H（ω）在ω=0、2π处为零，即H（z）在z=1处有一个零点，因此，如果数字滤波器在ω=0、2π处不为零，例如低通滤波器、带阻滤波器，则不能用这类数字滤波器来设计。

由于sin[ω（n-1/2）]对ω=0、2π呈奇对称，对于ω=π呈偶对称，因此，H（ω）对ω=0、2π呈奇对称，H（ω）对于ω=π也呈偶对称。

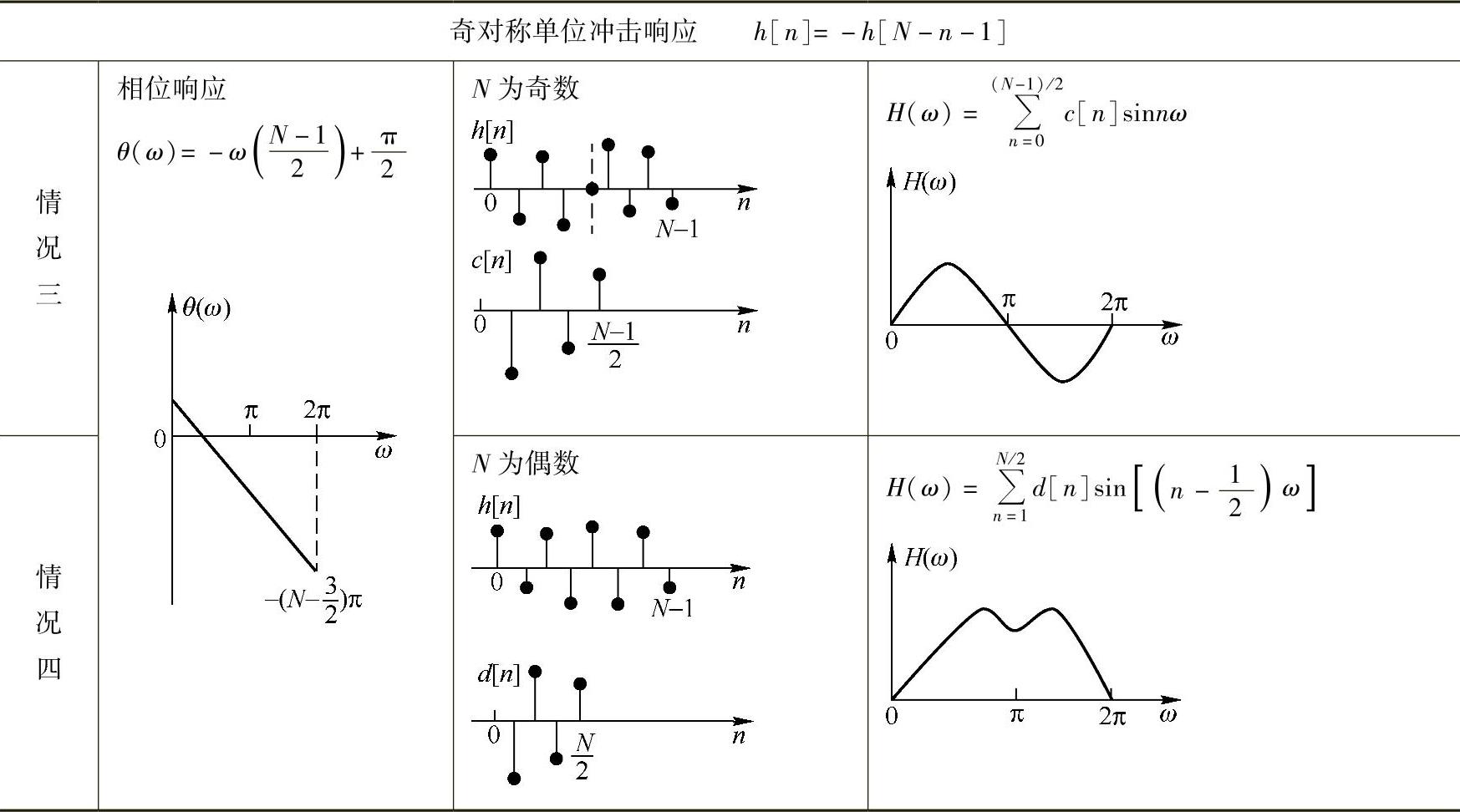
以上四种情况的h[n]、H（ω）、a[n]、b[n]、c[n]、d[n]、θ（ω）示于表6.2.1中。

由上述讨论可知，上述四种有限冲激响应滤波器的相频特性只取决于h[n]的对称性，而与h[n]的值无关。它们的幅度标量特性取决于h[n]，故在设计这类滤波器时，在保证h[n]对称的条件下，只考虑幅度的逼近即可。第一、二种情况的滤波器可以做一般意义下的有限冲激响应滤波器，而第三、四种情况的滤波器不适于做一般的滤波器，适于做希尔伯特变换器、微分器和正交网络。

从式（6.2.8）和（6.2.13）可以看出，h[n]不但均为奇对称（对于α=（N-1）/2点），而且在n＜α的主瓣区内（时域）的h[n]为负值，其对应的c[n]，d[n]也为负值。如果对H（ω）取绝对值，便得幅频特性，即|H（ω）|=|H（jω）|，与H（ω）相比，至少在ω＜π的范围内差一负号，致使相频特性θ（ω）变为

θ（ω）=θ（ω）-π=-π/2-（N-1）ω/2

表6.2.1 四种线性相位有限冲激响应滤波器的幅频特性和相频特性

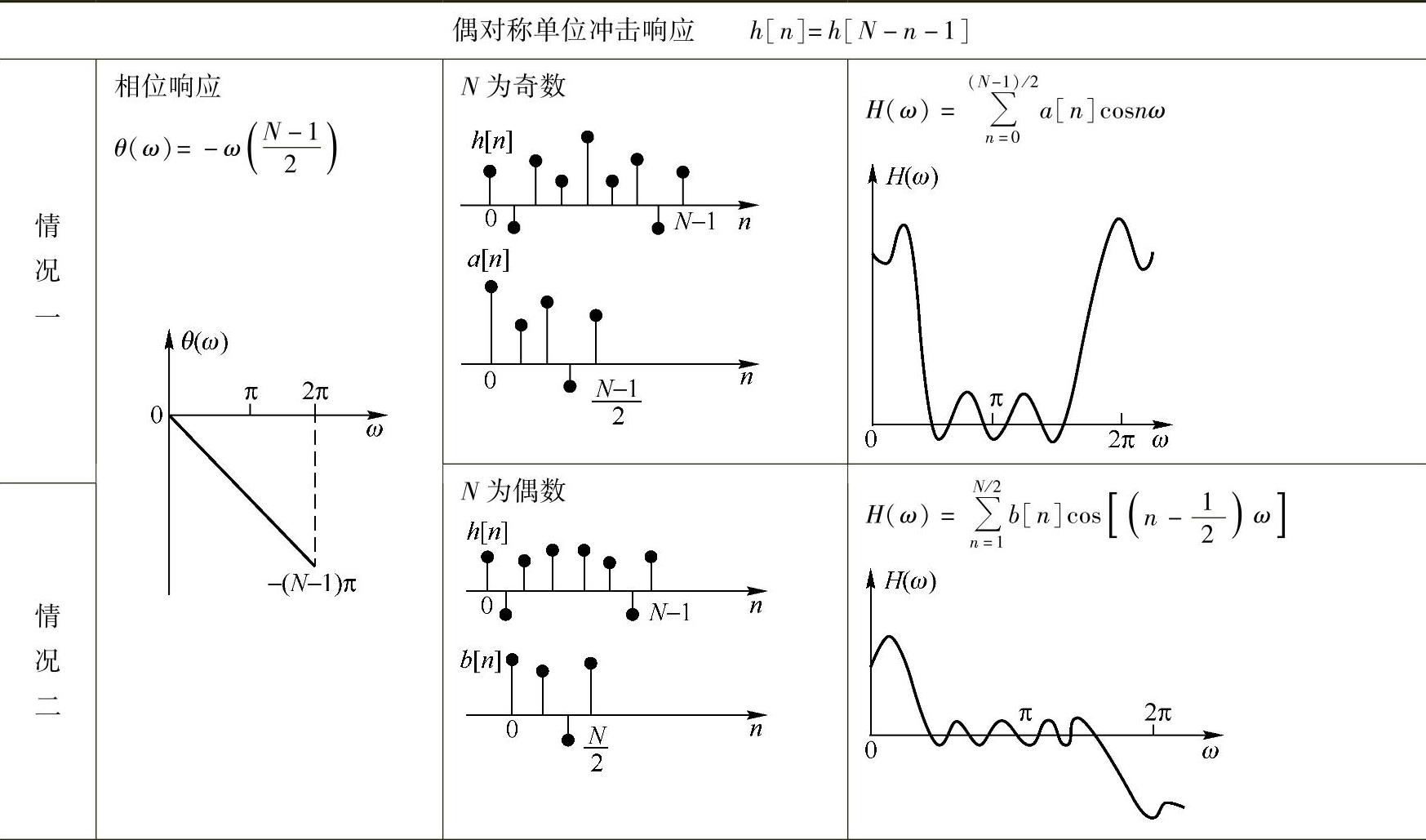
（续）