常用有限冲激响应滤波器特点与线性相位条件

在讨论线性相位有限冲激响应数字滤波器的条件之前，先讨论几种常用有限冲激响应滤波器的特点。这些滤波器既包括了一般意义下的高通、低通、带通等数字滤波器，也包括希尔伯特（Hilbert）变换器和微分器。

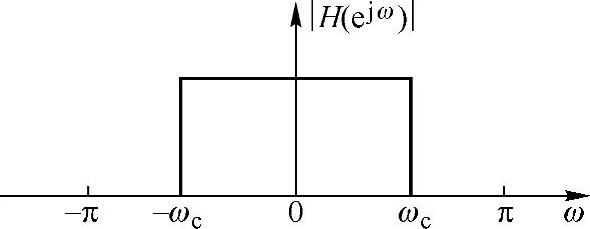
图6.2.1 理想低通滤波器的幅频特性

1.低通滤波器的时域特性

理想低通滤波器的幅频特性如图6.2.1所示。

不妨假设相频特性是φ（jω）=0，则理想滤波器的频率特性是

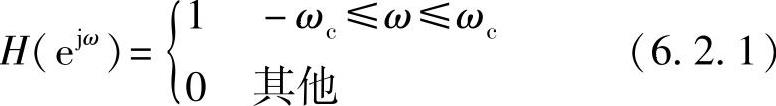
可求得其单位抽样响应为

如图6.2.2所示。

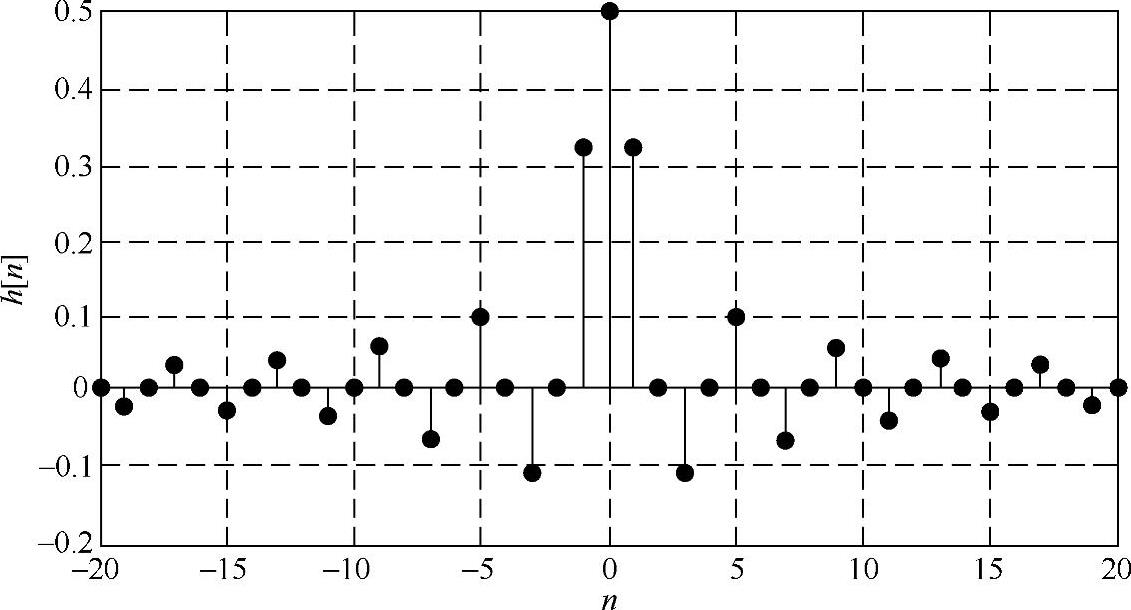
图6.2.2 理想低通滤波器的单位抽样响应（ω_c=π/2）

显然，理想低通滤波器的单位抽样响应h_d[n]=sin（ω_cn）/（nπ）是偶对称、无限长的。

同样，理想高通、带通等一般滤波器的单位冲激响应h_d[n]也是偶对称的。将h_d[n]延迟α=（N-1）/2后，以α为中心对称截取N点而得h[n]。则满足关系式h[n]=h[N-1-n]，即h[n]关于对称中心α=（N-1）/2是偶对称的。

位移后，滤波器的频率响应近似为

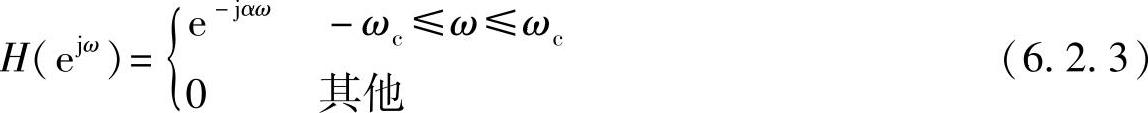
可见，其相频特性是线性的。

同理，可以证明具有线性相频特性θ（ω）=-ωα的理想高通、理想带通滤波器的时域响应也满足h[n]=h[N-1-n]。

2.希尔伯特滤波器的时域特性

理想希尔伯特滤波器的频率特性为

其幅频特性及相频特性如图6.2.3所示。

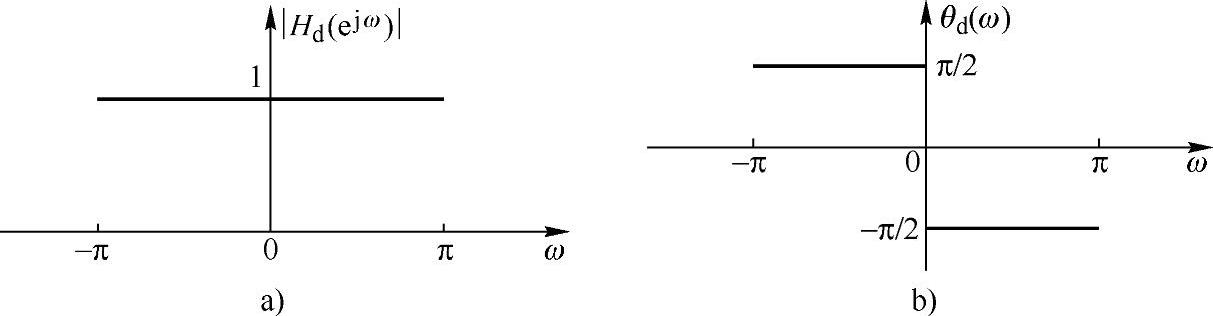
图6.2.3 希尔伯特滤波器的频率特性

a）幅频特性 b）相频特性

其单位抽样响应为

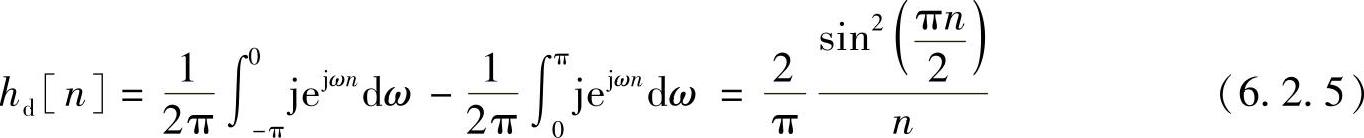(www.xing528.com)

显然，它是奇对称的。将其右移α=（N-1）/2后，频率特性为

相应的单位抽样响应为

以α=（N-1）/2为中心，对称截取N点得

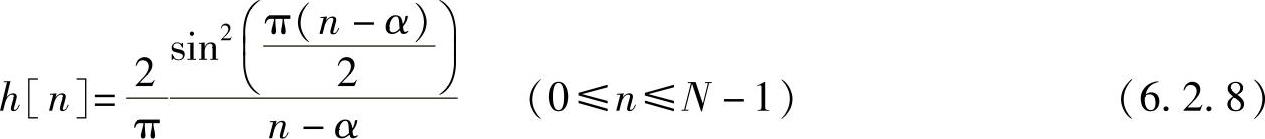
满足关系式h[n]=-h[N-1-n]，即是奇对称的。相应的频率特性如式（6.2.6）所示。可见，其相频特性为

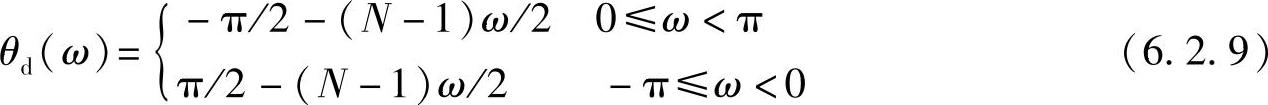
显然是线性的。

3.理想微分器

理想微分器的频率特性如图6.2.4所示。

将理想微分器的单位抽样响应位移α=（N-1）/2后的频率特性为

H_d（e^jω）=jωe^{-j（N-1）ω/2} （-π≤ω＜π） （6.2.10）

其相频特性是线性的，即

θ_d（ω）=π/2-（N-1）ω/2 （-π≤ω＜π） （6.2.11）

单位抽样响应为

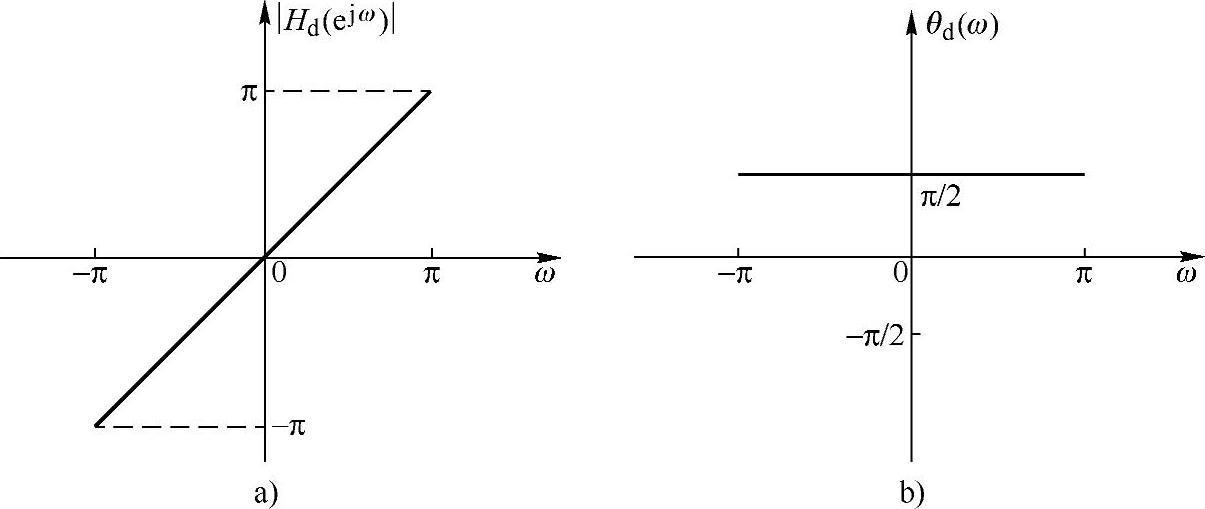
图6.2.4 理想微分器的频率特性

a）幅频特性 b）相频特性

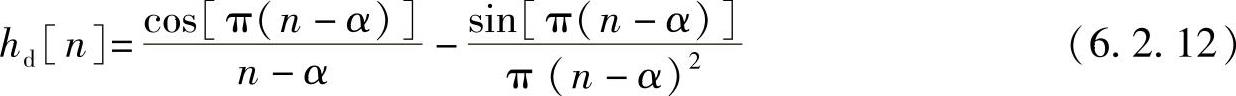
显然，它是奇对称序列。以α=（N-1）/2为中心，将其对称截取N点得

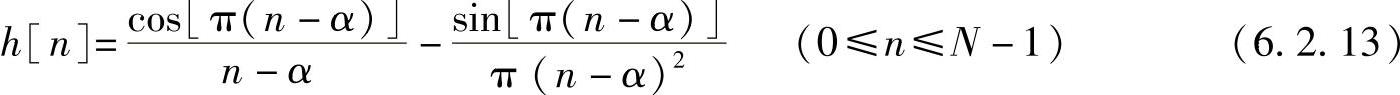
满足关系式h[n]=-h[N-1-n]，即是奇对称。

由以上分析可见，对一般意义下的具有线性相位的滤波器，它们的单位抽样响应满足

h[n]=h[N-1-n] （6.2.14）

或 h[n]=-h[N-1-n] （6.2.15）但是这是在几种特殊情况下导出的结论。下面，证明这个结论对于任何线性相位有限冲激响应滤波器都是成立的，或者说，若有限冲激响应滤波器满足式（6.2.14）或式（6.2.15），则有限冲激响应滤波器的相频特性一定是线性的。即式（6.2.14）或式（6.2.15）称为有限冲激响应滤波器的线性相位条件。