频域直接设计法实现无限冲激响应滤波器

前面介绍的无限冲激响应滤波器的设计方法是借助于经典的模拟滤波器的现有成果，然后用不同的变换方法，把s域特性映射为z域特性，从而得到所设计的数字滤波器。这种设计方法得到的滤波器频率特性形状是固有的几种，而且都只适用于频率特性具有选择性的场合。在某些应用情况下，当要设计的滤波器频率特性不是很规则时则用直接设计法，它是在某种最小化误差准则下，用计算机求解线性或非线性方程组，来确定滤波器各参数。所以也叫做计算机辅助设计或最优化设计。

对无限冲激响应滤波器，在频域直接逼近比较好的误差准则是最小均方误差准则（除此之外还有r误差准则法、线性规化法等）。施泰格利茨（Steiglitz）在20世纪70年代利用这一准则提出了一种无限冲激响应滤波器的设计方法。该方法是采用二阶节级联形式的数字网络去逼近给定的滤波器幅频特性，选用二阶节级联形式的原因主要是频率特性对系数的变化（即系数的量化误差）影响不大，也就是网络特性对系数变化的敏感度低；另外，在优化过程中比较容易计算幅频特性对各参数的导数。

设要求的滤波器幅频特性为H_d（e^jω），待设计滤波器的幅频特性由下面的数字网络决定，即

设计指标要求是在指定一组离散频率{ω_i}（i=1，2，…，M）上，使幅频响应误差的二次方和最小，即

把式（5.6.1）表示的H（z）代入式（5.6.2）中，得

令误差的二次方和E对A的偏导数等于零，得

求得A的最佳值为

当A=A_opt时，E对参数A取得最小值。

二阶节的分子、分母各系数可以组成一个矢量，令φ_k=[a_k，b_k，c_k，d_k]^T，则E对φ_k中各元素的偏导数统一记为(www.xing528.com)

式中，

根据式（5.6.3）可具体求出E对a_k，b_k，c_k，d_k的偏导数，即有

把式（5.6.7）表示的4K个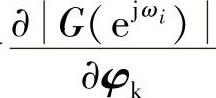代入式（5.6.5），就得到4K个关于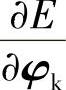的非线性方程，即

k=1，2，…，K，如果表示成矢量形式，则有

解式（5.6.9）的非线性方程组通常用递归迭代的方法，可以利用弗莱彻-鲍威尔（Fletcher-powell）的优化算法求解。计算误差函数的梯度，由此搜索误差函数的最小值。一般由给定的初始值开始寻求它的最小值，当两个相邻的E（φ，A）值的差值在10^-4～10^-5以内时停止迭代，此组（φ，A）即为要求的解。

这个过程中对零、极点无任何限制，有可能使零、极点落在单位圆外。假定极点z=z_i，z_i为实数，z_i＞1，则可以利用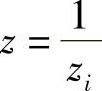极点来替代。原函数乘以（z-z_i）/（z-1/z_i）分式，该分式是一个全通函数使得单位圆外的零极点相互抵消，而把单位圆外的极点变成单位圆内的极点。这样可以保证滤波器是稳定的，而幅频特性与给定的设计要求相差一个比例常数。

这种频域均方误差最小的逼近方法的优点是可以以给定的误差要求逼近任意形状的幅频特性，灵活性强。缺点是需要解一组非线性方程，因而计算比较繁杂。