数字频率域的频率变换原理及应用

第二种方法比第一种方法灵活，因为模拟低通滤波器原型变换成数字低通滤波器原型时，不受变换方法的限制。下面讨论第二种方法。

设数字低通滤波器原型的系统函数为H_l（z），通过数字频率变换

z=G（Z） （5.5.13）

得到另一个数字滤波器系统函数H_l[G（Z）]，此系统函数即为所希望的系统函数H（Z），即

H_d（Z）=H_l[G（Z）] （5.5.14）

从式（5.5.13）可以看出，数字频率变换实际上就是从z平面到Z平面的映射，这一映射必须满足下列条件。

1）单位圆变换到单位圆，即

e^jθ=G（e^jω）=e^{jarg[G（ejω）]} （5.5.15）

式（5.5.15）表明，z平面与Z平面角频率间存在一定的关系，同时可知G（e^jω）=1，说明G（Z）是全通函数。

2）如果H_l（z）是稳定的并且具有最小相位，那么要求H（Z）也是稳定的，并且具有最小相位。因此若Z=Z_p是H（Z）的极点（或零点），则G（Z_p）必定是H_l[G（Z）]的极点（或零点）。由稳定性Z_p＜1，要求G（Z_p）＜1，因此作为变换函数有下列关系，即

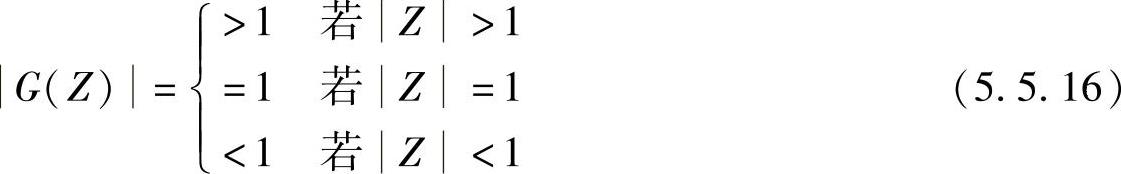
式（5.5.16）说明，频率变换函数的自乘G₁（Z）G₂（Z）仍是变换函数，其复合函数G₁[G₂（Z）]也是变换函数。

3）由于IIR滤波器的系统函数是有理函数，因而经过变换后的H（Z）也必然是有理函数，即G（Z）应是有理函数。

能够满足上述三个条件而作为数字频率变换函数的有理函数是

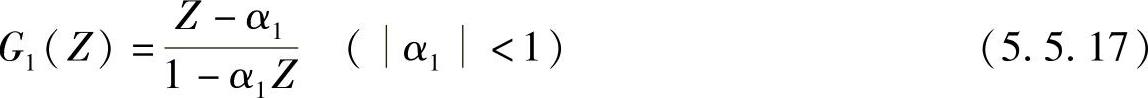
由式（5.5.17）可得

这是稳定的全通函数，而且用它来替代低通滤波器原型结构的延时环节z^-1，就可以得到要求的数字滤波器低通到低通的变换。

由于任意一个频率变换函数的自乘仍是频率变换函数，所以一般形式可以表示为

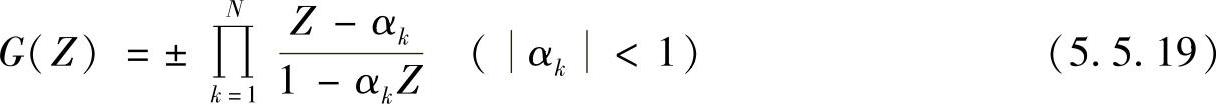
对式（5.5.19）展开得

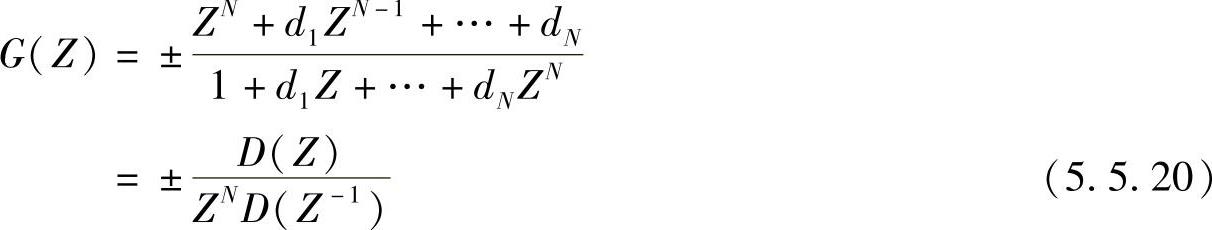
这就是各种数字滤波器所需的频率变换函数。根据辐角原理，z平面中的单位圆按反时针方向绕单位圆一周，相当于在z平面上绕了N周，这样才能映射出N个带通的滤波器。所以根据要求变换的滤波器的通带个数可以确定G（Z）的阶次N。例如要使原型数字滤波器映射成带通或带阻滤波器，也就是在单位圆上（0～2π之间）要具有两个通带，那么单位圆必须映射其自身两次，即N=2。下面就低通、高通、带通、带阻四种情况具体计算G（Z）有理式中的多项式系数d_i。

1.低通到低通的变换

这种情况下映射其自身单位圆只一次，因此N=1，且

变换条件为

式中，θ_p和ω_p分别为低通原型和要求的低通数字滤波器的截止频率。将式（5.5.22）代入式（5.5.21）有

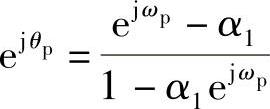
则

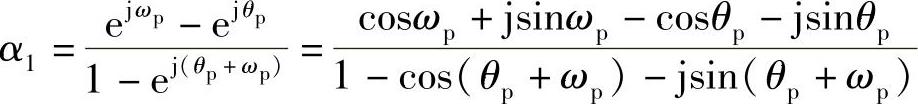
实部、虚部对应相等，有α₁[1-cos（θ_p+ω_p）]=cosω_p-cosθ_p，求得

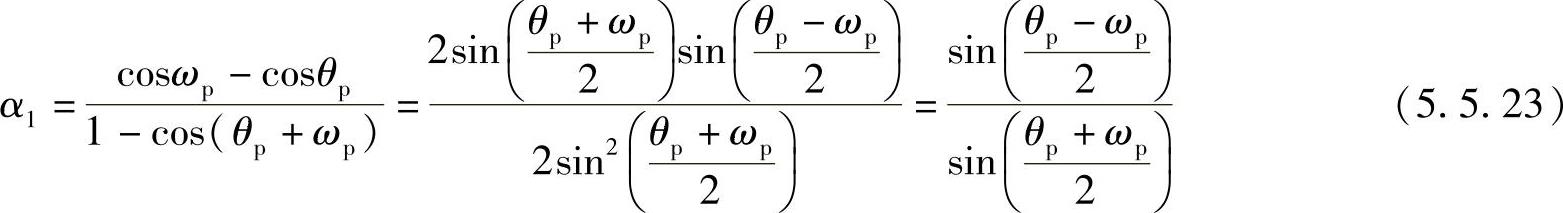
对应变换关系如图5.5.5所示。

2.低通到高通的变换

和低通一样，单位圆映射其自身只有一次，因而取N=1，对应的变换关系如图5.5.6所示。

变换条件为

由式（5.5.24）的第一个变换条件可知，应取变换函数的形式为

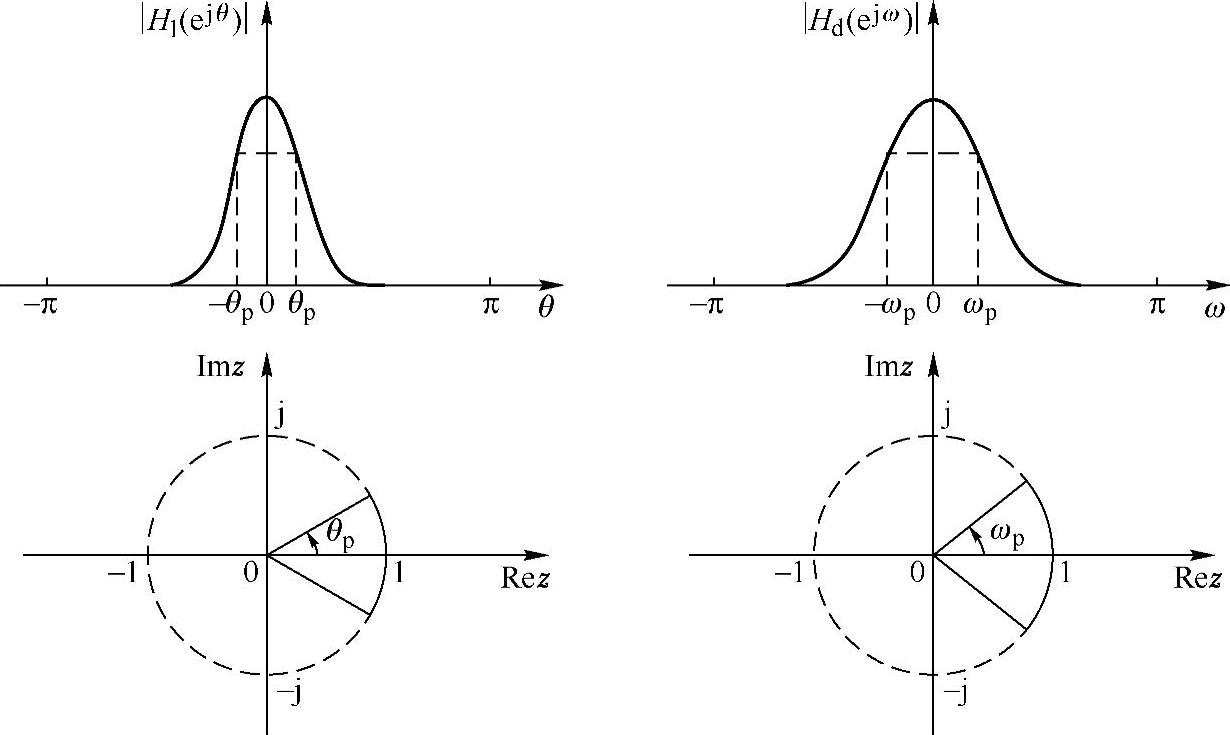
图5.5.5 低通到低通的变换

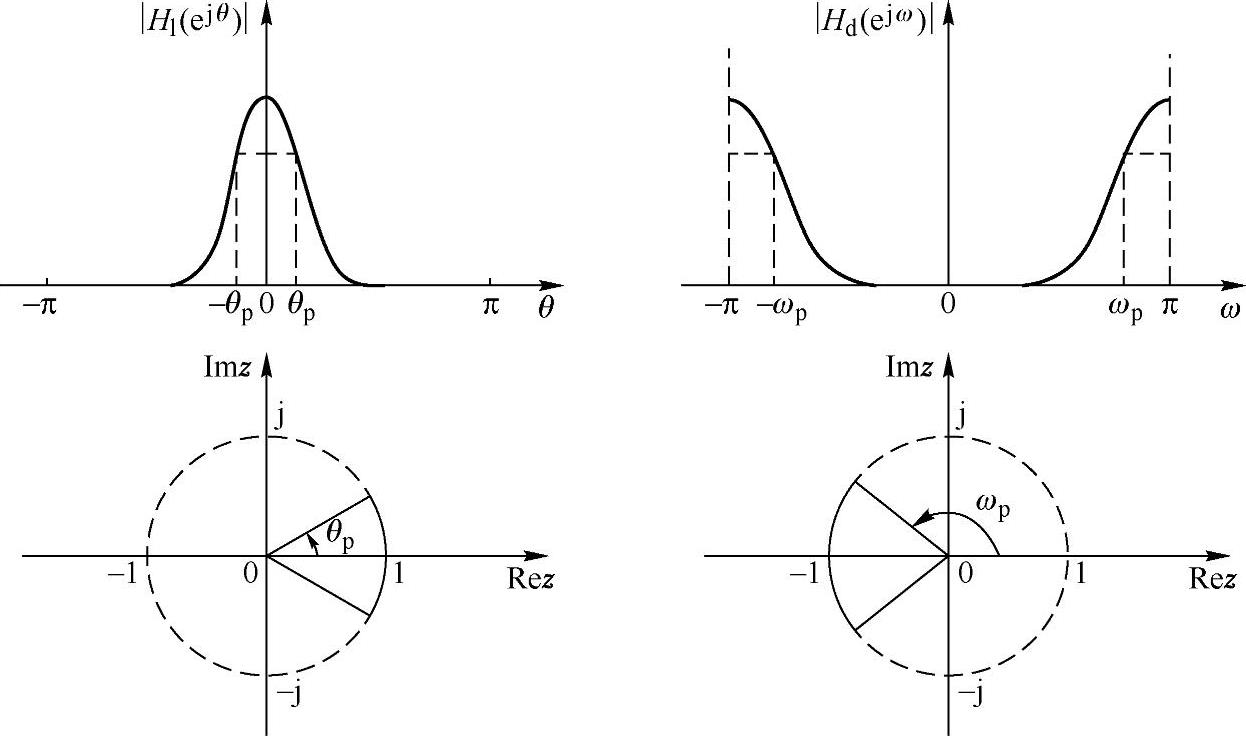
图5.5.6 低通到高通的变换

又由式（5.5.24）的第二个变换条件可得

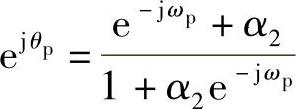
实部、虚部对应相等，求得

3.低通到带通的变换

低通到带通的变换关系，如图5.5.7所示。由于在0～2π范围内形成两个通带，也就是变换函数需要映射其单位圆本身两次，因而对式（5.5.20）表示的变换函数取N=2。同时带通变换可以看成低通变换和高通变换的组合，所以取

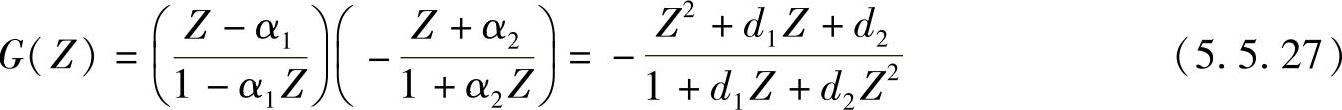
变换条件为

式中，ω₀为带通滤波器中心频率，ω₂，ω₁分别为带通滤波器上、下截止频率。

将式（5.5.28）代入式（5.5.27），得

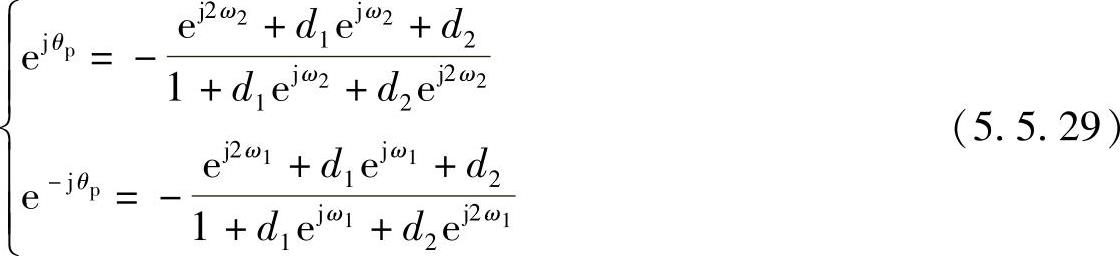
整理得

解此联立方程得

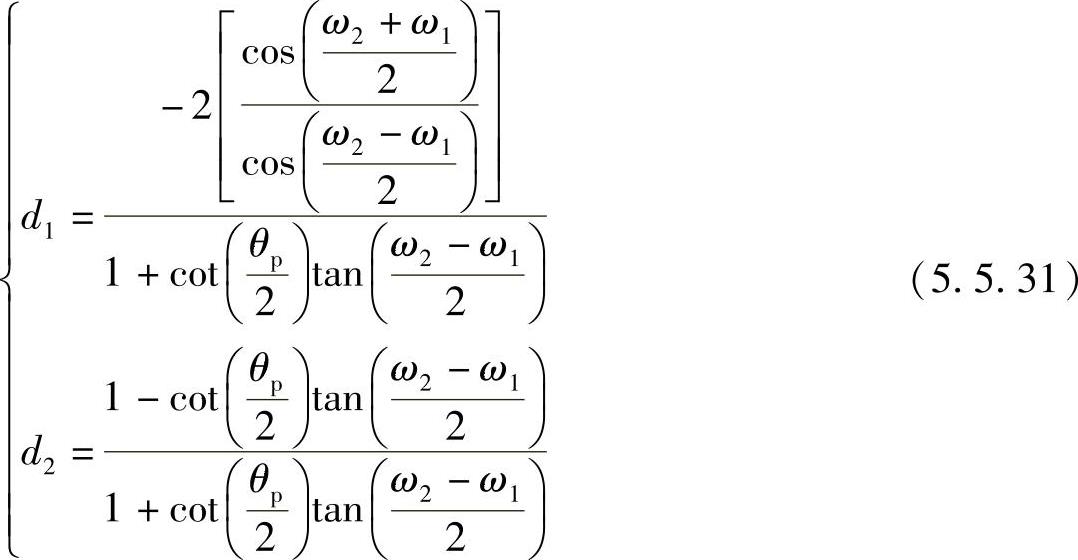
如果式（5.5.31）中令

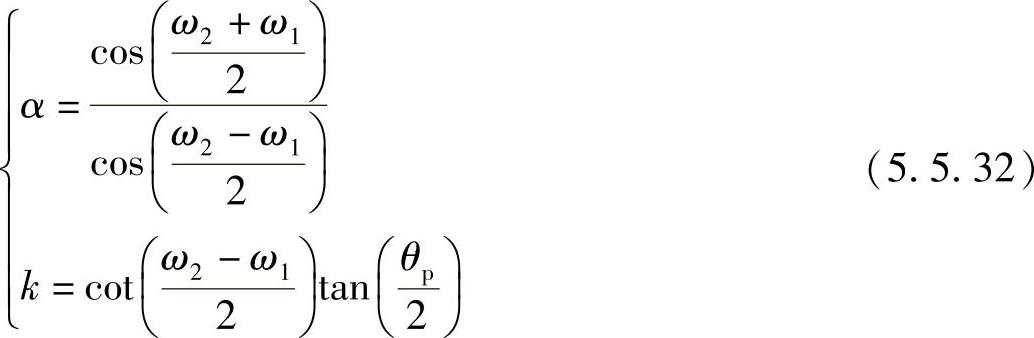
则变换式（5.3.31）中的d₁及d₂可以表示成

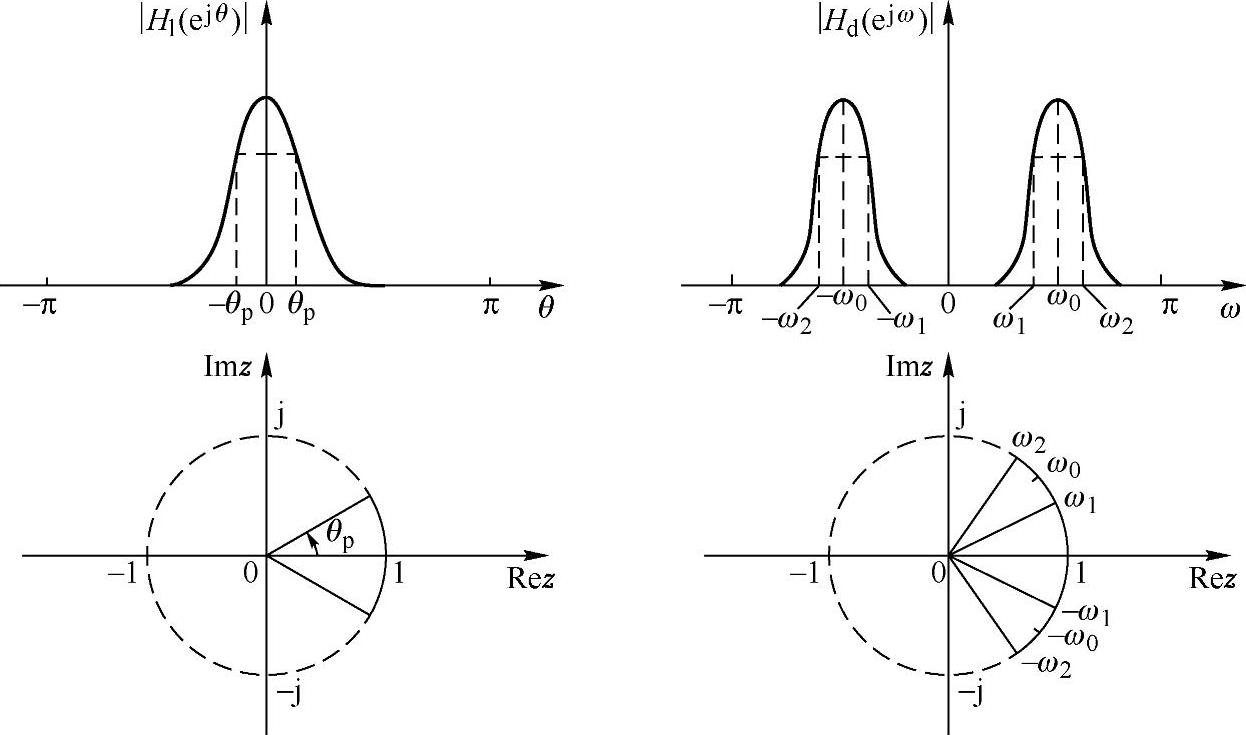
图5.5.7 低通到带通的变换

4.低通到带阻的变换

低通到带阻的变换关系，如图5.5.8所示。由于带阻的中心频率在ω₀，在高端和低端各形成通带范围，据此变换函数需要映射其单位圆本身两次，因而取N=2。又由于在ω=0处形成通带，因而取变换函数形式为

变换条件为

式中，ω₁，ω₂分别为带阻滤波器上、下截止频率。由第一个变换条件决定了G（Z）取“+”号的形式，由第二、第三个变换条件可以得到

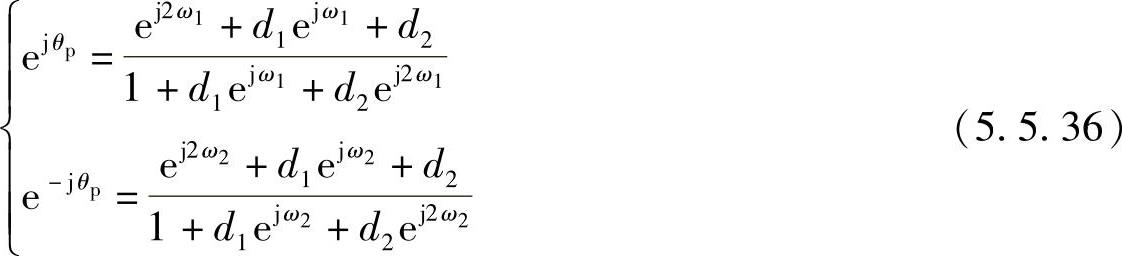
整理得

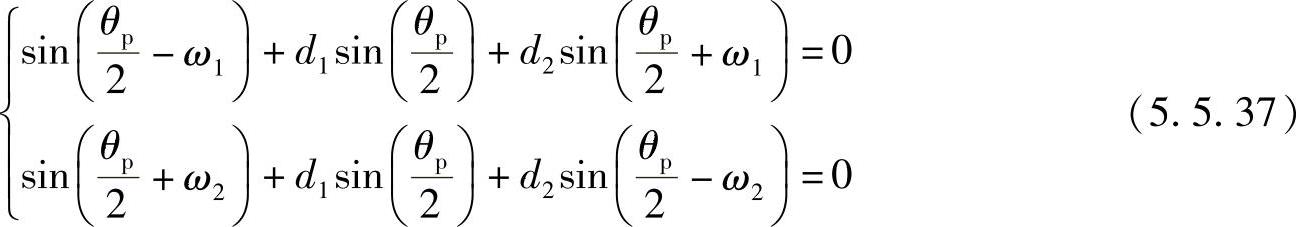
解此联立方程得

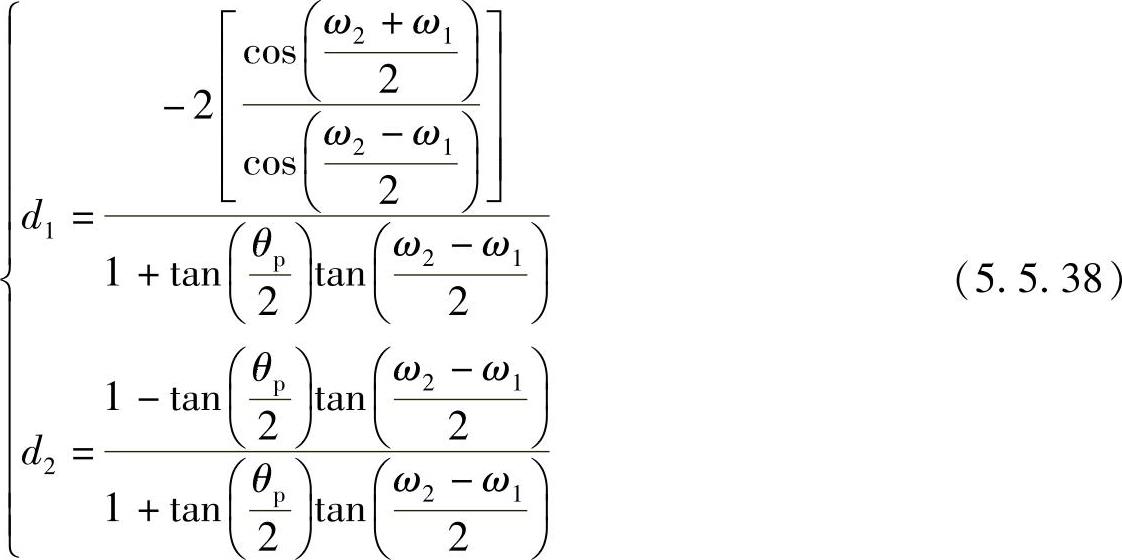
如果式（5.5.38）中令

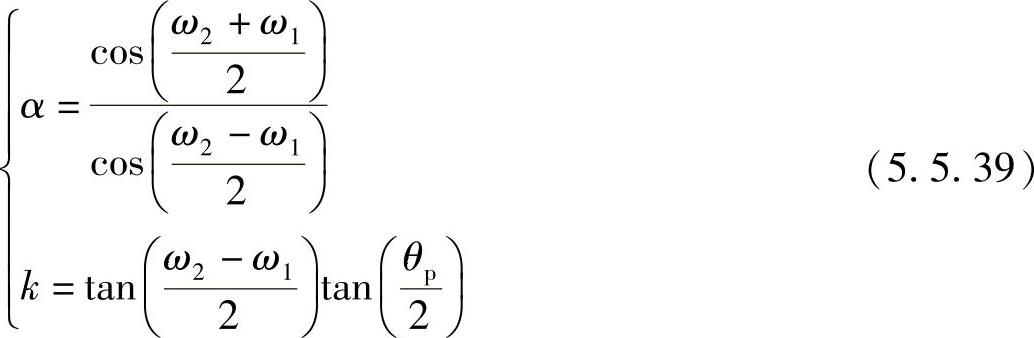
则式（5.5.38）变换式中的d₁及d₂可以表示成

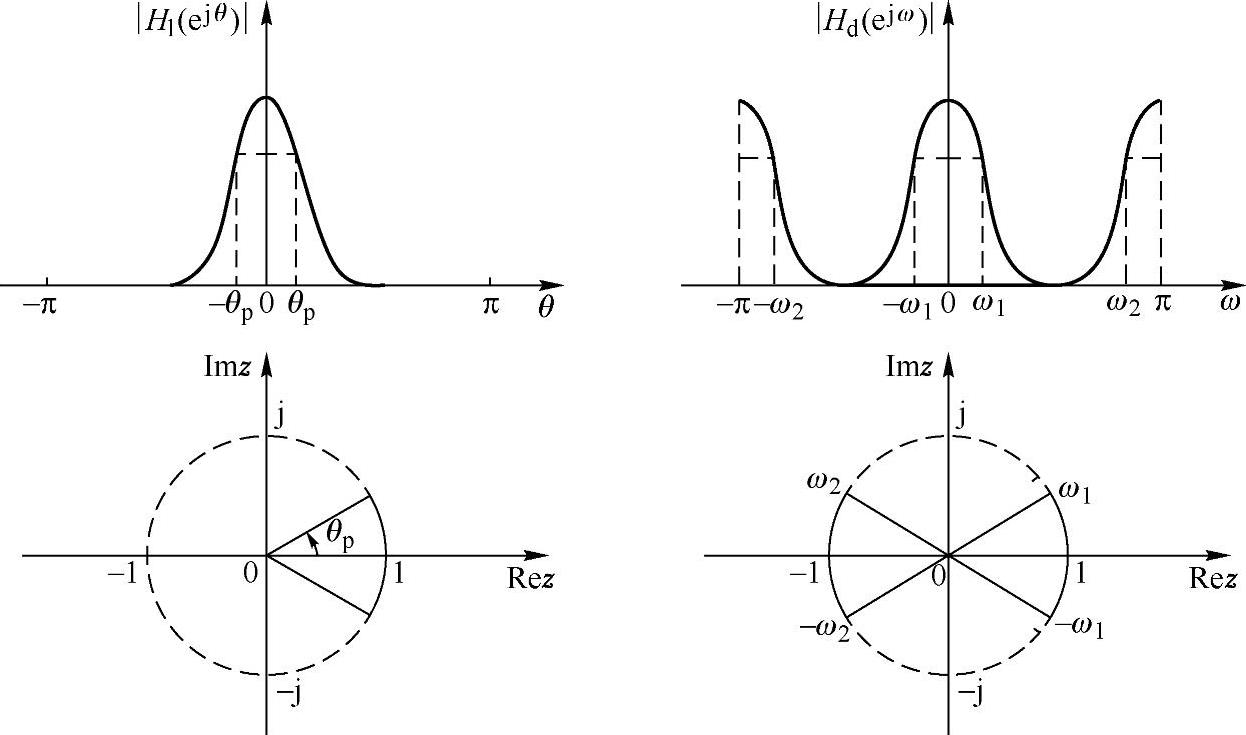
图5.5.8 低通到带阻的变换

以上对低通原型到低通、高通、带通及带阻情况的讨论可以推广到多通带的情况。变换函数阶数N的选取决定于0～2π范围内通带的数目，而变换函数G（Z）符号的选择取决于ω=0是通带情况还是阻带情况。

当ω=0是阻带情况（例如高通、带通），此时变换函数选择成

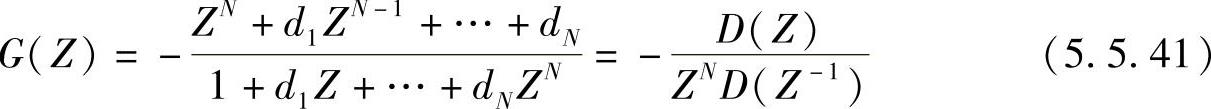
0～2π范围内共有N个通带，所有通带两两对ω=0纵轴成镜像对称关系。每一通带可以找出对应于低通原型上下截止频率±θ_p的对应点。由此关系即可求出G（Z）中的N个系数d_k（k=1，2，…，N）。设第i个通带的上边带ω_i2对应原型上边带θ_p，则有(www.xing528.com)

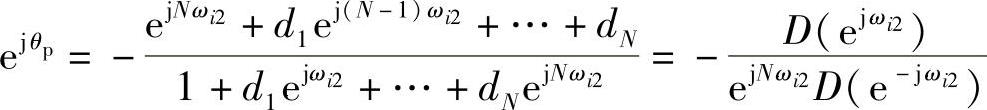
或

e^jθpe^jNωi2D（e^-jωi2）+D（e^jωi2）=0

对应的d_k项合并，有

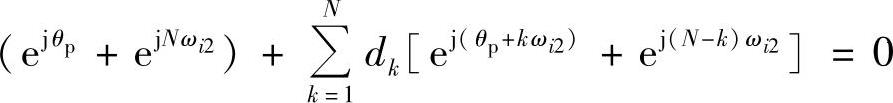
整理化简得

同理，第i个通带的下边带ω_i1对应原型下边带-θ_p，从而得出如下的方程

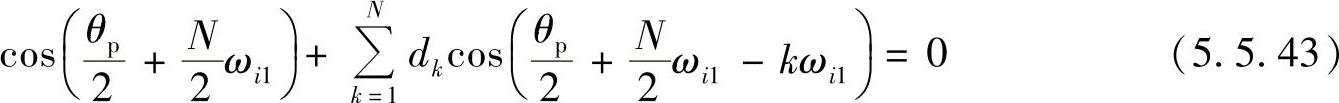
对0～π间的通带可以得出N个方程（此时1≤i≤N/2），联立求解N个方程即可解出d₁，d₂，…，d_N的N个系数，由此可以求出要求的变换函数。

对于ω=0是通带的情况（例如低通、带阻），变换函数选择成

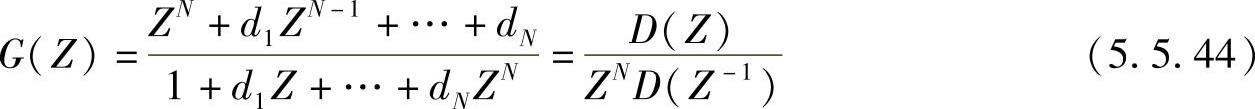
同理可以推导出方程组

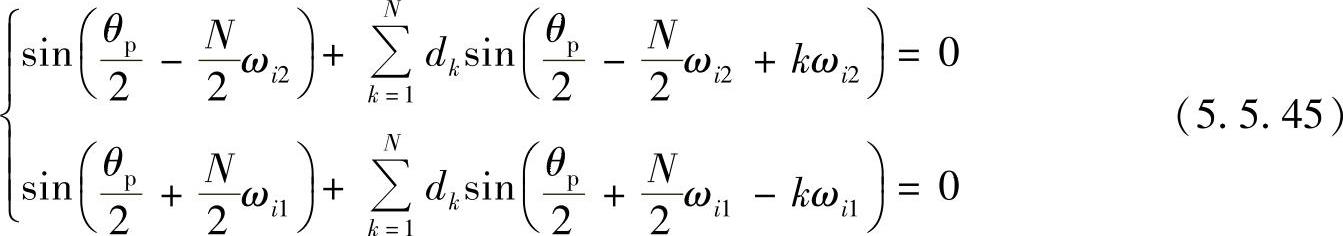
式中，1≤i≤N/2，解此方程即可求出要求的N个系数d_k（k=1，2，…，N）。

表5.5.1列出了各种情况的数字频率变换关系式，供设计参考。

表5.5.1 数字频率变换关系式

（续）

以上讨论的数字频率变换与双线性变换非常相似，都是一种频率间的非线性变换。例如对于式（5.5.21）所表示的低通到低通的变换函数，求θ与ω间的关系，则有

解式（5.5.46）得ω与θ的关系为

图5.5.9画出了这一表示式的相应图形。当θ_p≠ω_p（θ_p=ω_p即为原型自身）时，ω_p与θ_p间呈现非线性关系，它将导致变换后频率特性形状的失真。

【例5.5.4】 要求设计一带通数字滤波器，给定指标如下：通带内允许起伏1dB，0.45π≤ω≤0.55π；阻带衰减≤-15dB，0≤ω≤0.3π，0.7π≤ω≤π。用通带等波纹滤波器逼近，求该滤波器的系统函数H_d（Z）。

解 1）求对应的模拟带通滤波器指标，其特性如图5.5.10所示。为避免混叠，采用双线性变换，按双线性变换频率预畸变要求，得

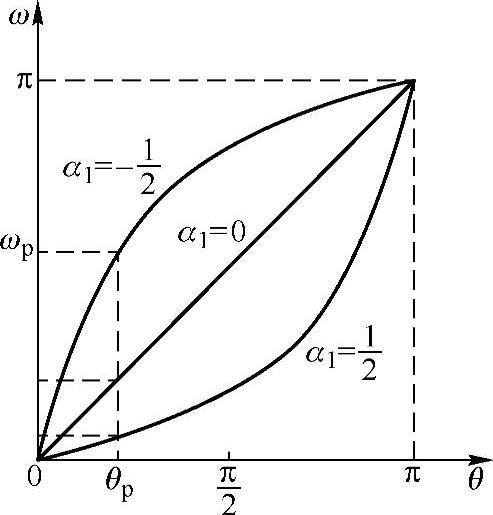
图5.5.9 低通到低通变换的频率刻度畸变

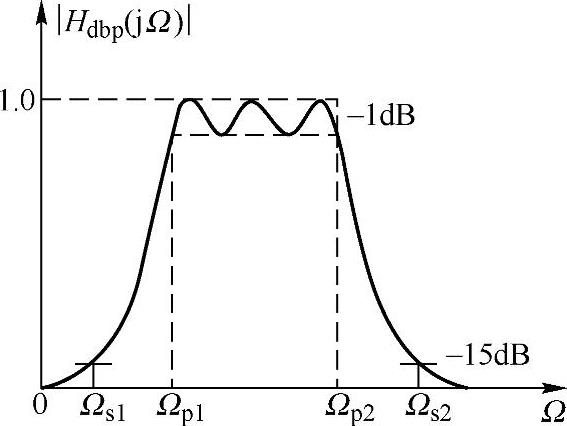
图5.5.10 模拟带通滤波器的设计要求

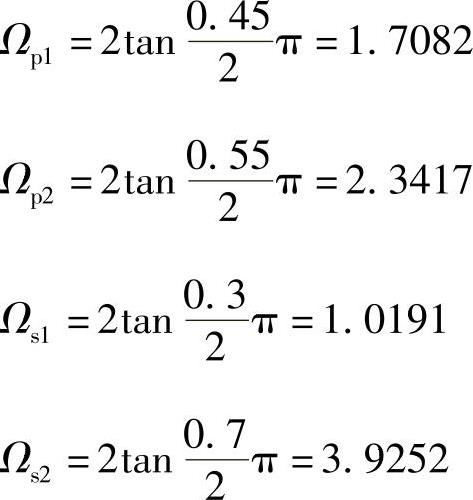
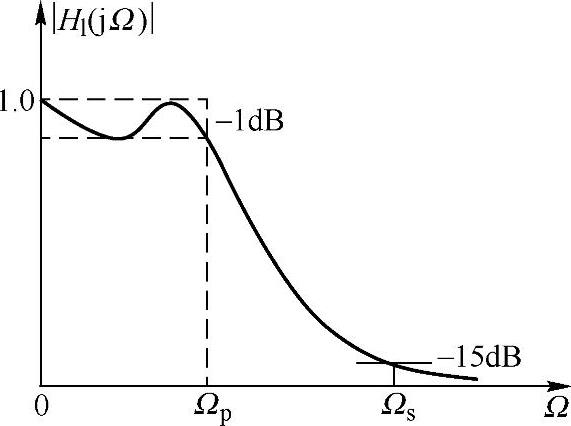
图5.5.11 模拟低通原型特性

2）求归一化模拟低通原型滤波器，其特性如图5.5.11所示。首先按模拟带通滤波器频率变换关系，求归一化模拟带通滤波器各边界频率β_p1，β_p2，β_s1，β_s2。

B=Ω_p2-Ω_p1=2.3417-1.7082=0.6335于是归一化模拟带通滤波器各边界频率为

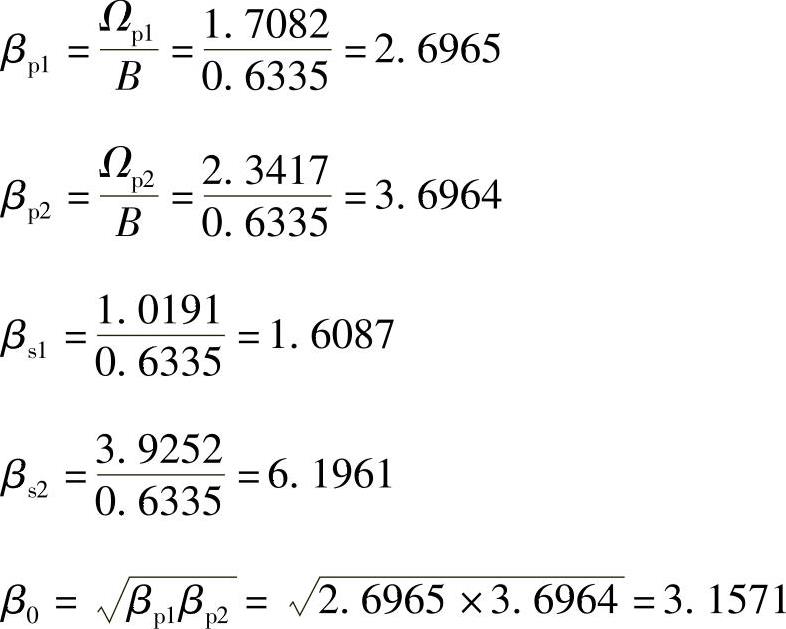
则低通原型的通带边界频率为

λ_p1和λ_p2是归一化低通原型的通带边界频率，因而其值取1。

低通原型的阻带边界频率为

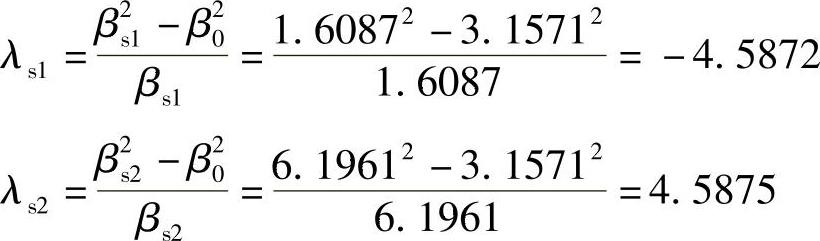
取频率稍低的λ_s1=4.5872，以保证满足阻带衰减。

由此可以求出通带等波纹低通原型的各参数如下：

滤波器阶数，取N=2，则滤波器极点分布

短轴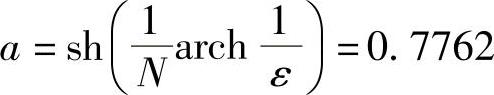

长轴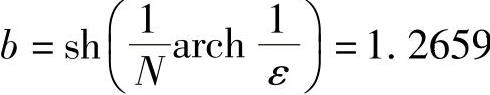

极点为

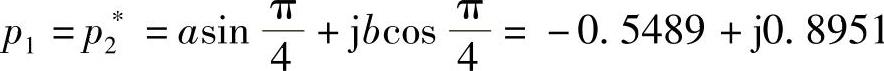
则低通原型模拟滤波器的系统函数为

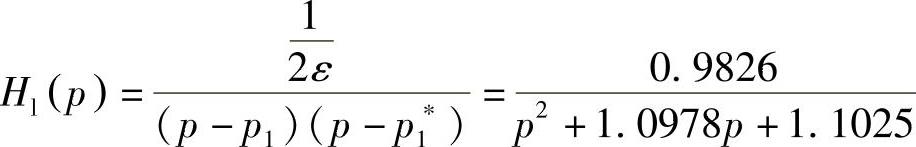
3）求数字低通原型滤波器的转移函数H_l（z）。

利用双线性变换把模拟低通原型滤波器转换成数字低通原型滤波器，取T=1，用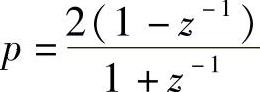代入H_l（p）得

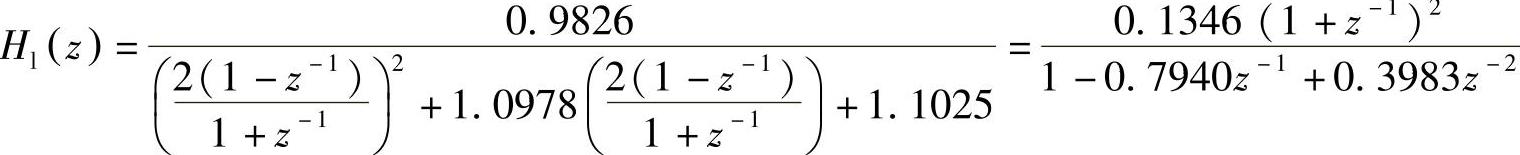
其频率特性如图5.5.12所示。

4）利用带通频率变换求H_d（Z）。

数字低通原型滤波器截止角（频率）为

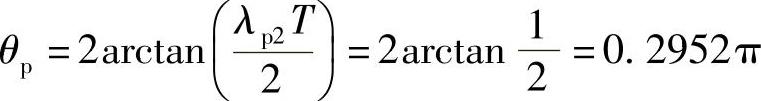
根据式（5.5.32）求出

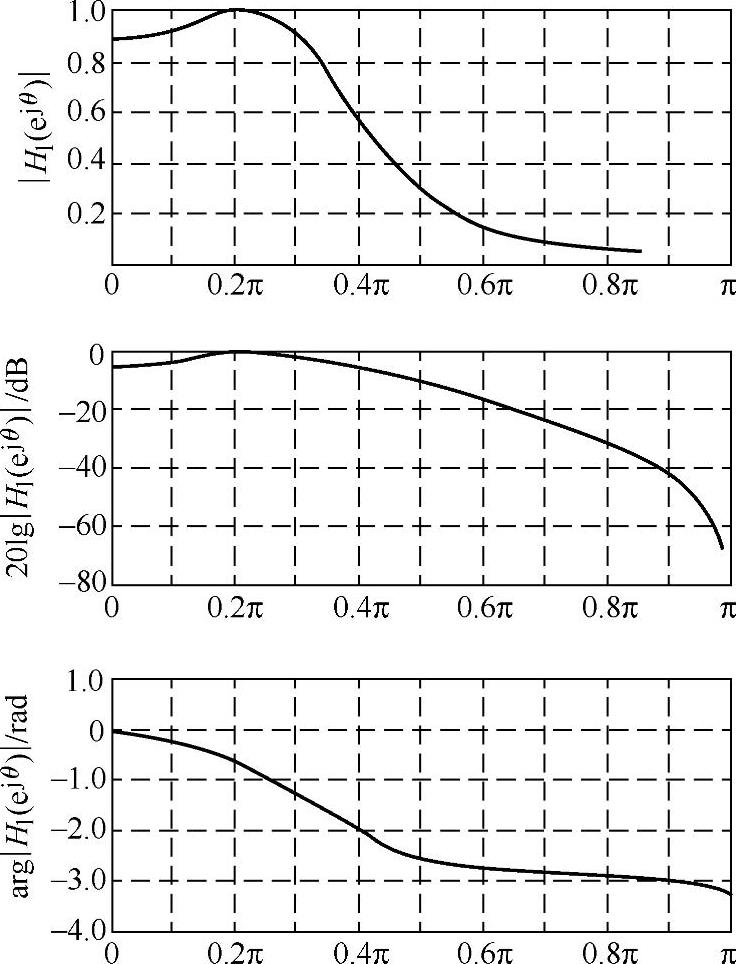
图5.5.12 数字低通原型滤波器的频率特性

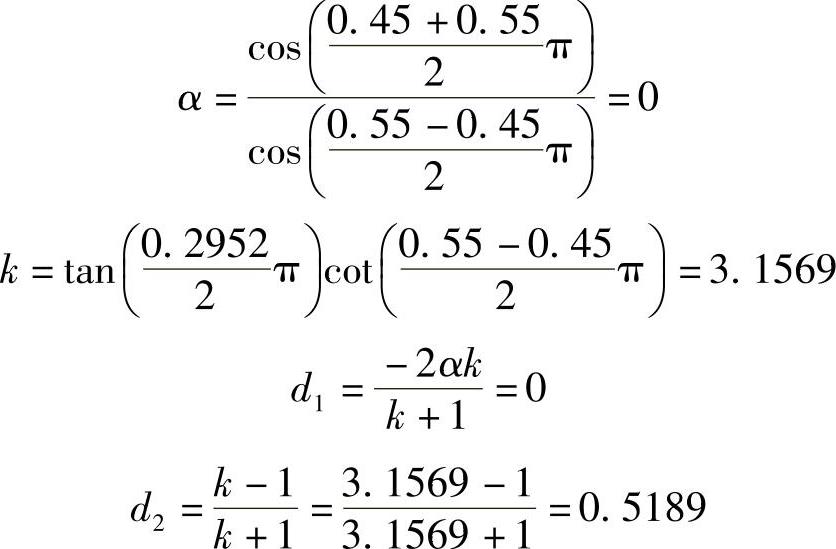
由表5.5.1变换公式求出

或

把上式代入H_l（z）的表达式中，即得要求的H_d（Z）为

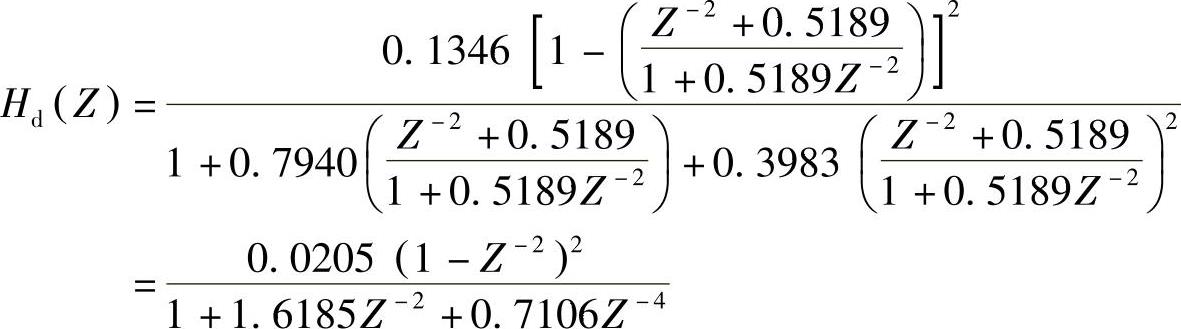
图5.5.13是对应的数字带通滤波器的频率特性。

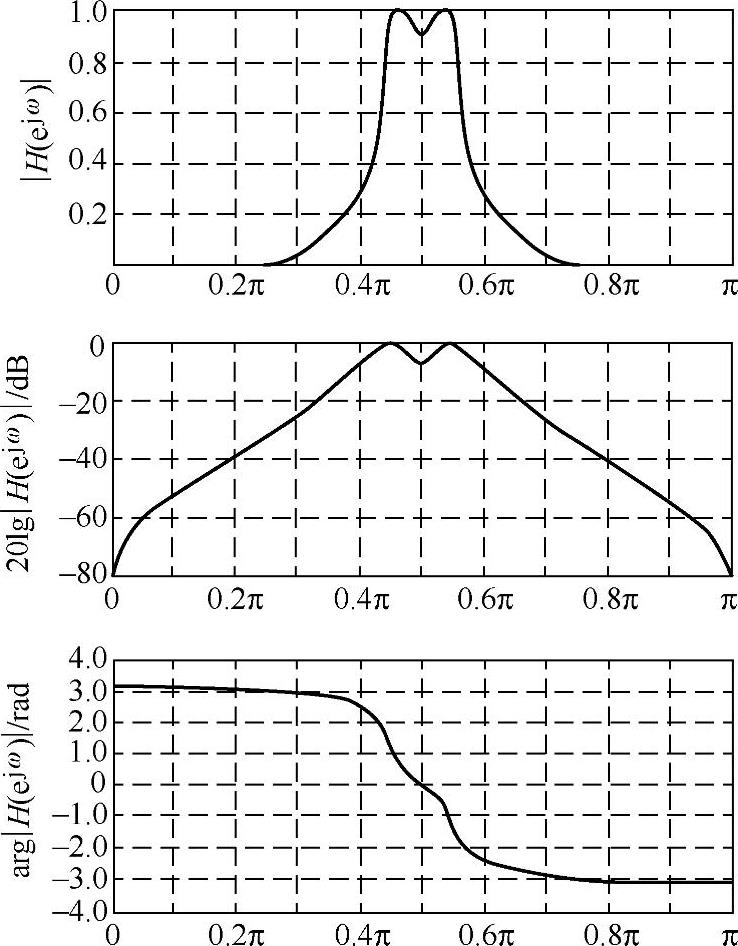
图5.5.13 数字带通滤波器的频率特性

【例5.5.5】 要求设计一数字滤波器，给定0～π间的两个通带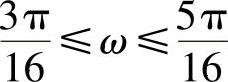：和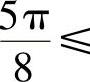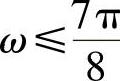。用图5.5.12所示滤波器作为数字低通原型滤波器，求该双通带滤波器的系统函数H_d（Z）。

解 这是一个多通带频率变换，由于要求的是双通带，因而取频率变换式为

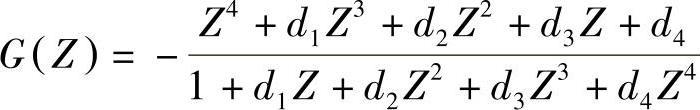
且由例5.5.1知θ_p=0.2952π。另有，，，。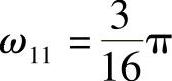

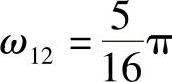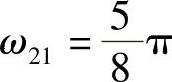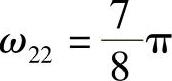把θ_p和ω_i1，ω_i2（i=1，2）分别代入式（5.5.42）和式（5.5.43），得到一组关于d_k（k=1，2，3，4）的联立方程

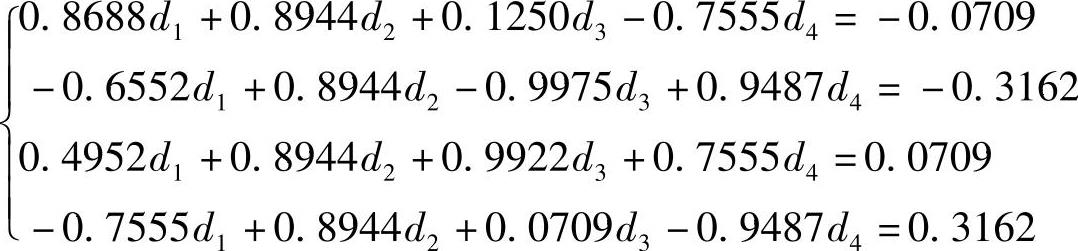
解此联立方程得

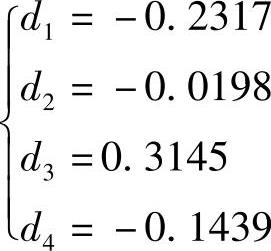
因而要求的数字频率变换为

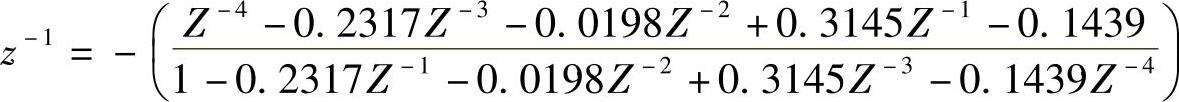
把上式代入例5.5.1中3）的低通原型表示式H_l（z），并整理得出本例要求的双通带数字滤波器系统函数为

其对应的频率特性如图5.5.14所示。从图中可以看出，由于数字频率变换是一非线性变换，即θ与ω之间是非线性关系，因而当要求变换的频率范围比较宽时，变换后的频率特性与原型低通的频率特性相比较，存在明显的频率特性形状失真。

图5.5.14 双通带数字滤波器的频率特性