借助低通滤波器的系统函数,经合适的频率变换,可以得到高通、带通、带阻滤波器的系统函数,因此不论哪一种滤波器的设计,都可以先将该滤波器的技术指标转化为频率归一化的低通滤波器的技术指标,按照该指标先设计低通滤波器的系统函数,再通过频率变换,得到所需类型的系统函数,对所得系统函数数字化即得到所需类型的数字滤波器。
频率变换也可直接用于无源滤波电路,把低通滤波电路通过适当的元器件变换转化为其他类型的滤波电路。
为了叙述方便,定义p=η+jλ为低通原型滤波器Hl(p)的归一化复变量,其通带边界频率记为λp,λ称为归一化频率。用Hd(s)表示希望设计的模拟滤波器的系统函数,s=σ+jΩ表示Hd(s)的复变量,其归一化复变量q=α+jβ。下面介绍各种频率变换公式。从p域到s域映射的可逆变换记为p=F(s)。低通系统函数Hl(p)与Hd(s)之间的转换关系为

1.低通到高通的变换
低通到高通的变换关系为

Ωc是高通滤波器的3dB截止频率,在虚轴(频率轴)上该变换关系简化为如下的频率变换
公式

令归一化频率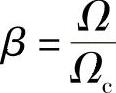 ,代入上式得
,代入上式得
λβ=-1 (5.5.4)
由于物理可实现滤波器的幅频特性具有偶对称特性,故低通到高通的频率对应关系可表示为
λβ=1 (5.5.5)
这样,由要求的高通滤波器技术指标即可求出对应的低通原型滤波器的指标要求,从而得出Hl(p)。把p=jλ代入Hl(p),即可得到低通原型频率特性Hl(jλ)。由低通原型的系统函数Hl(p)通过式(5.5.3)的复频率变换就可以得到要求设计的高通滤波器的系统函数Hdhp(s)。图5.5.2描绘了低通到高通的频率变换关系。

图5.5.2 低通原型到高通的边界频率和幅频响应特性的变换关系
图中,βp为希望设计的高通滤波器Hdhp(s)的归一化通带边界频率,βs为归一化阻带边界频率。
以二阶巴特沃斯低通滤波器的变换为例,其归一化系统函数为
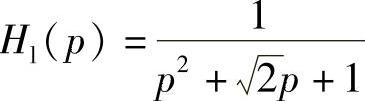
利用式(5.5.3),为简便计算取Ωc=1rad/s,则变换后的系统函数为

【例5.5.1】 设计巴特沃斯模拟高通滤波器,其技术指标:通带内起伏1dB,通带边界频率Ωp=2π×1.5×104rad/s,阻带衰减≤15dB,阻带边界频率Ωs=2π×104rad/s。
解 1)求高通滤波器的归一化各频率。

2)求低通原型滤波器的归一化各频率,应用式(5.5.4),有
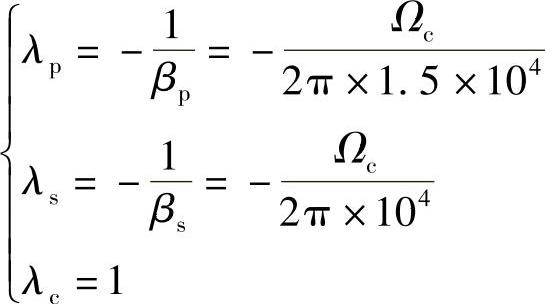
因而低通原型滤波器的技术指标为
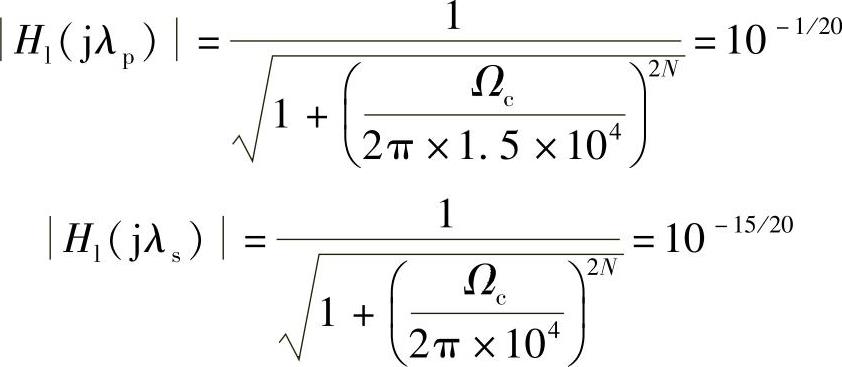
3)确定N,求低通原型滤波器的Hl(p)。

取N=6,λc=1,则左边平面的6个极点为
p1=p∗6=ej105°
p2=p∗5=ej135°
p3=p∗4=ej165°
求得

4)求高通滤波器的Hdhp(s)。根据低通原型特性,先确定3dB截止频率,利用阻带频率λs有
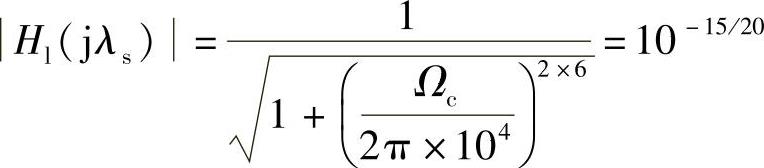
解得
Ωc=2π×1.33×104
用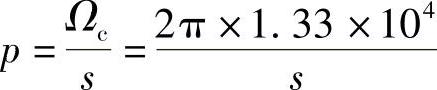 代入Hal(p)的表达式,得
代入Hal(p)的表达式,得
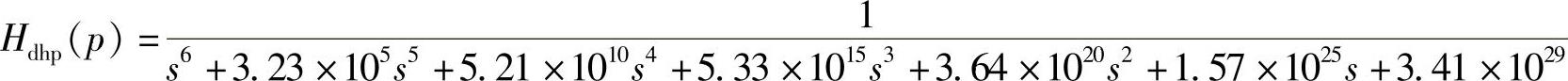
2.低通到带通的变换
低通到带通的变换关系为

式中,B=Ωp2-Ωp1,Ω02=Ωp1Ωp2。将式(5.5.7)代入低通原型滤波器的系统函数Hl(p),就可以得到要求设计的带通滤波器的系统函数Hdbp(s),即

将p=jλ、s=jΩ代入式(5.5.7),并将所有频率对带宽B进行归一化,得

式(5.5.9)即为低通原型滤波器和希望设计的带通滤波器两者归一化频率间应满足的关系。式中, ,
, 。图5.5.3是归一化低通原型与归一化带通频率的对应关系。
。图5.5.3是归一化低通原型与归一化带通频率的对应关系。

图5.5.3 低通原型到带通的边界频率和幅频响应特性的变换关系
【例5.5.2】 给定带通滤波器的技术指标是:通带内(Ωp1≤Ω≤Ωp2)允许起伏3dB,Ωp1=2π×1.5×104rad/s,Ωp2=2π×2.5×104rad/s;阻带内(Ωs2≤Ω≤Ωs1)衰减≤15dB,Ωs2=2π×3×104rad/s,Ωs1=2π×104rad/s。用巴特沃斯滤波器实现,求该滤波器的系统函数Hdbp(s)。
解 1)求归一化带通滤波器频率。
B=Ωp2-Ωp1=2π×104rad/s
 (https://www.xing528.com)
(https://www.xing528.com)
则各归一化频率为
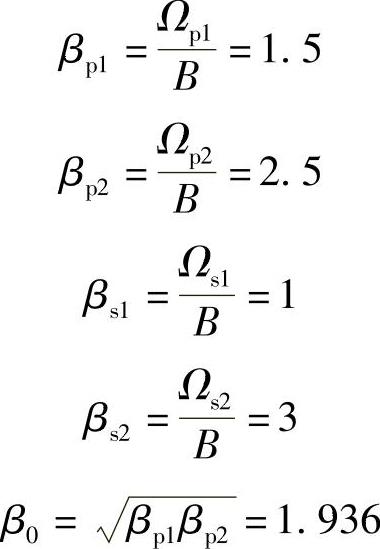
2)求低通原型各归一化频率。
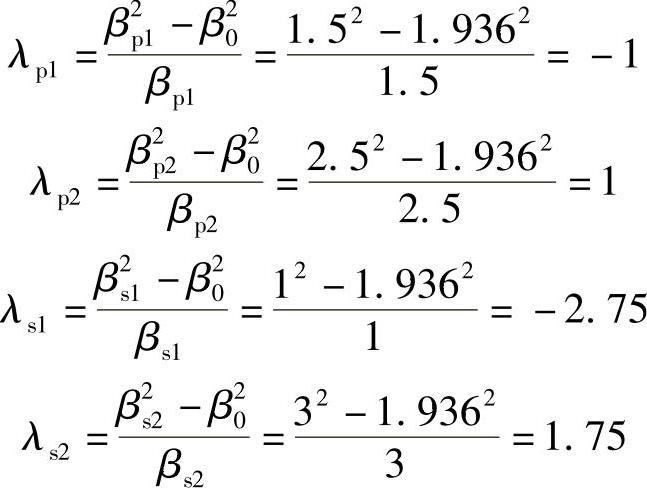
这里两边阻带频率不等,是由于低通到带通是非线性变换。
3)求低通原型滤波器的系统函数Hl(p)。由于λs1≠λs2,为保证指标取λs2=1.75,则有
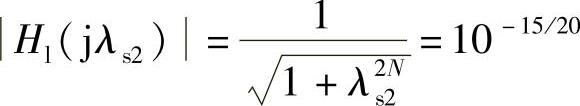
解得滤波器的阶数为
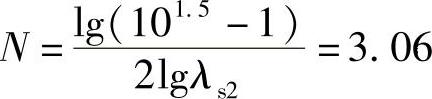
取N=4。各极点分别为
p1=p∗4=ej112.5°
p2=p∗3=ej157.5°
要求的低通原型滤波器的系统函数为
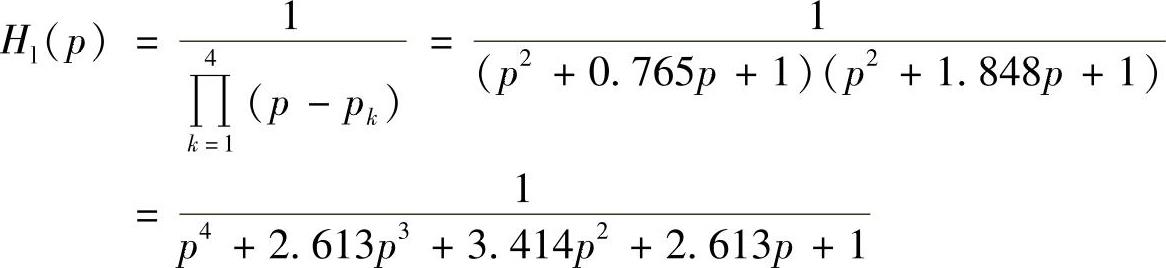
4)求带通滤波器的系统函数Hdbp(s)。
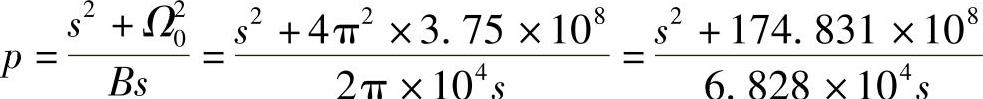
则

7.943×1015s5+1.731×1021s4+1.176×1026s3+1.595×1031s2+5.334×1035s+4.812×1040)
3.低通到带阻的变换
低通到带阻的变换关系为

式中,B=Ωp2-Ωp1,Ω20=Ωp1Ωp2。将式(5.5.10)代入低通原型滤波器的系统函数Hl(p),就可以得到要求设计的带阻滤波器的系统函数Hdbs(s),即
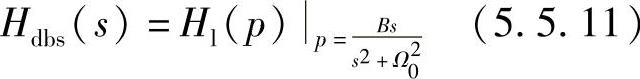
将p=jλ、s=jΩ代入式(5.5.10),并将所有频率对带宽B进行归一化,得

式(5.5.12)即为低通原型滤波器和希望设计的带阻滤波器两者归一化频率间应满足的关系。式中,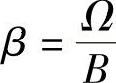 ,
,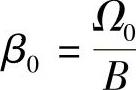 。图5.5.4是归一化低通原型与归一化带阻频率的对应关系。
。图5.5.4是归一化低通原型与归一化带阻频率的对应关系。
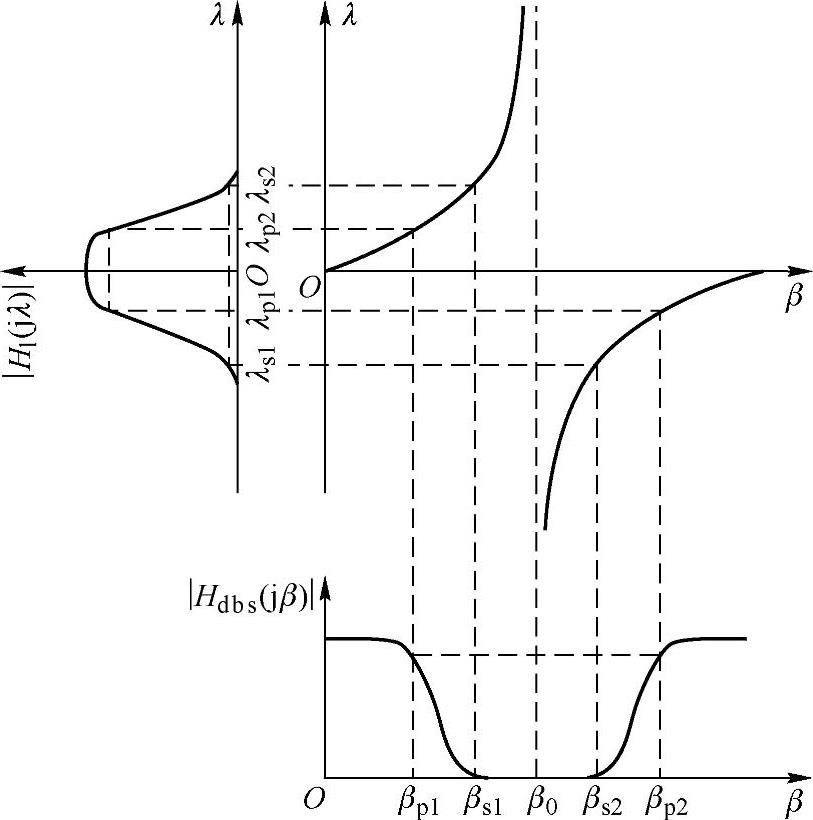
图5.5.4 低通原型到带阻的边界频率 和幅频响应特性的变换关系
【例5.5.3】 已知带阻滤波器的技术指标为:通带内(Ωp2<Ω<Ωp1)允许起伏1dB,Ωp2=2π×6×104rad/s,Ωp1=2π×4×104rad/s;阻带内(Ωs1<Ω<Ωs2)衰减≤15dB,Ωs1=2π×4.5×104rad/s,Ωs2=2π×5.5×104rad/s。用切比雪夫滤波器实现,求该带阻滤波器的系统函数Hdbs(s)。
解 1)求带阻滤波器的各归一化频率。
B=Ωp2-Ωp1=2π×2×104rad/s
则各归一化频率为
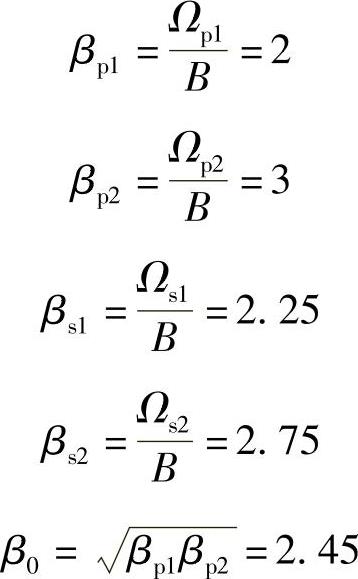
2)求低通原型滤波器的各归一化频率。
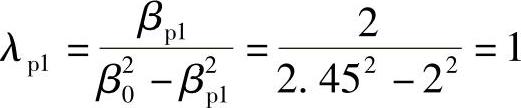

由于频率变换的非线性及相对带宽比较宽,因而低通原型滤波器正负频率两边特性不对称,在设计时为保证指标要求采用min[λs1,λs2],因而取λs=1.76,λp=λp1=1。
3)求低通原型滤波器的系统函数。依题意有
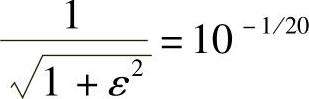
解得
ε=0.50885
于是
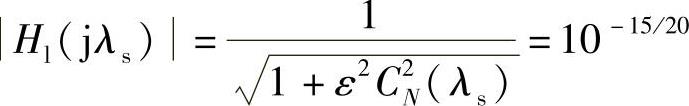
从而求得阶数
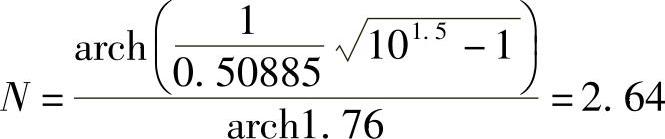
取N=3。椭圆参数的短轴a和长轴b分别为
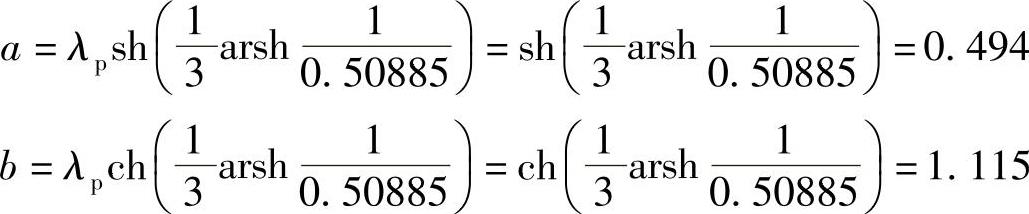
各极点为

那么低通原型滤波器的系统函数为

4)求带阻滤波器的系统函数Hdbs(s)。
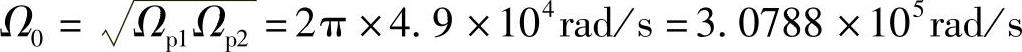

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




