冲激响应不变法的优缺点分析

1.优点

1）频率变换是线性关系，ω=ΩT，数字滤波器可以很好地重现模拟滤波器的频响特性。

2）数字滤波器的单位抽样完全模仿模拟滤波器的单位抽样响应，时域特性逼近好。

2.缺点

1）有频谱混叠失真现象（s平面到z平面有多值映射关系）。

2）由于频谱混叠，使应用受到限制。采样周期T减小，失真减小，但运算量增加，实现困难。

【例5.3.1】 已知模拟滤波器的系统函数H_a（s）为

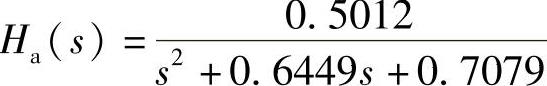
用冲激响应不变法将H_a（s）转换成数字滤波器的系统函数H（z）。

解 首先将H_a（s）写成部分分式

极点为

s₁=-（0.3224+j0.7772），s₂=-（0.3224-j0.7772）

根据z=e^sT，H（z）的极点为

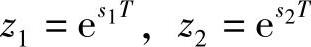
按照式（5.3.6），经整理，得到

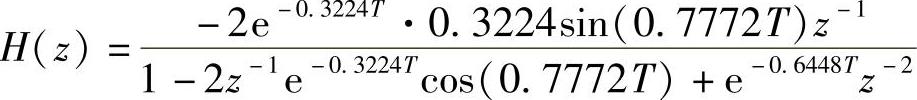
采样间隔T若选取过大，则会使ω=π附近频谱混叠现象严重。在此选取T=1s和T=0.1s两种情况进行比较。设T=1s时系统函数为H₁（z），T=0.1s时系统函数为H₂（z），那么

将H_a（jΩ）、H₁（e^jω）、H₂（e^jω）的幅度特性用它们最大值归一化后，得到它们的幅度特性曲线，如图5.3.4所示。

由图5.3.4a可见，模拟滤波器H_a（s）的通带很窄，但阻带衰减慢，拖了很长的尾巴，不是带限滤波器。图5.3.4b所示的是两种采样间隔（T=1s、0.1s），转换成数字滤波器的损耗函数，它的横坐标是对π归一化的数字频率。图5.3.4a、b两张图的横坐标服从线性关系即ω=ΩT。按照这种关系，T=0.1s时，图5.3.4a的A、B、C、D、E点对应图5.3.4b的a、b、c、d、e点；而T=1s时，图5.3.4a的H、I、J点对应图5.3.4b的h、i、j点。显然T=0.1s时，它们的幅度特性很相似，只是在折叠频率π（模拟频率是10π=31.42rad/s）附近有很轻的混叠现象。而对于T=1s情况，频率混叠现象很严重，原模拟滤波器在J点幅度衰减近26dB，而对应的数字滤波器的j点幅度衰减却只有18dB，J点的模拟频率只有3.142rad/s，J点附近失真更厉害。数字滤波器的幅度特性在ω=π以后又上升，是由于数字系统函数的周期性形成的。

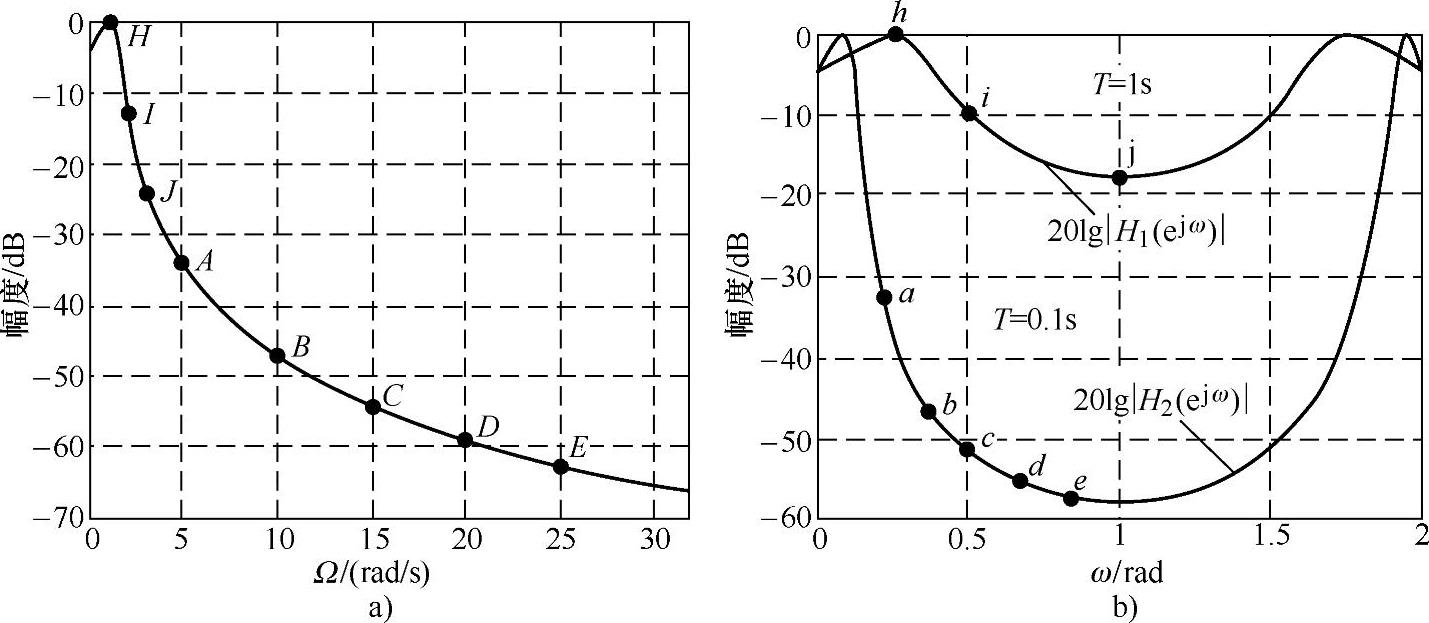
图5.3.4 例5.3.1中不同采样频率转换结果对比

【例5.3.2】 给定数字滤波器特性如下：通带内允许起伏1dB，0≤ω≤0.2π；阻带内衰减≤15dB，0.3π≤ω≤π。求该数字滤波器的系统函数。

解 利用冲激响应不变法设计，先把上述数字滤波器指标转换成模拟滤波器指标。为简单计令采样周期T=1，于是得模拟滤波器技术指标如下：

通带内允许起伏1dB，0≤Ω≤0.2π；阻带内衰减≤15dB，0.3π≤Ω≤π。

（1）用最大平坦滤波器（巴特沃斯滤波器）实现

首先确定模拟滤波器的阶数N和3dB截止频率Ω_c。根据指标要求有

解得N=5.8858，在此取N=6，即用6阶巴特沃斯滤波器实现。

考虑到冲激响应不变法在频率高端有混叠，所以在N=6的情况下，让通带满足要求，求出Ω_c，这样阻带指标会有富余，从而减小由于混叠带来的影响。据此有

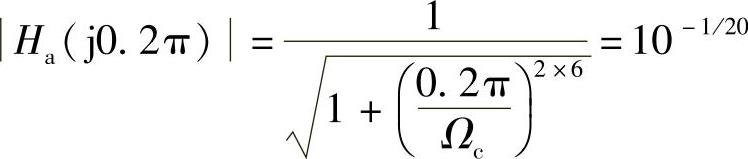
求得

Ω_c=0.7032

这样得到巴特沃斯滤波器的极点分布为

s₁=s^∗₆=0.7032e^j105°

s₂=s^∗₅=0.7032e^j135°(www.xing528.com)

s₃=s^∗₄=0.7032e^j165°

模拟滤波器的系统函数为

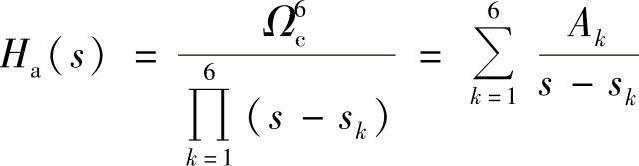
式中

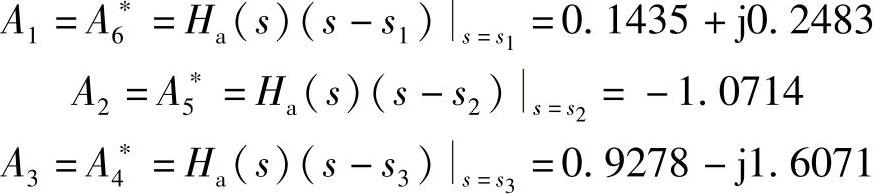
利用冲激响应不变法的映射关系式（5.3.7）得

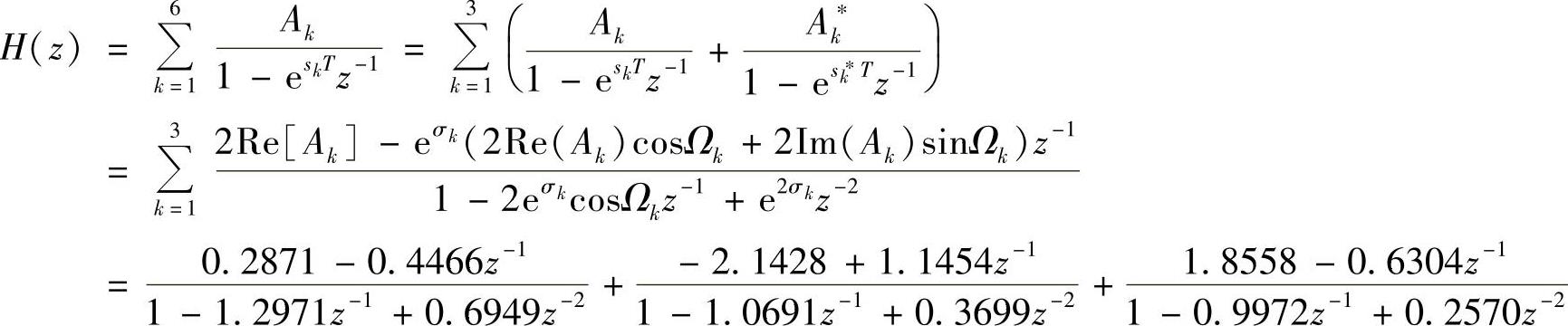
图5.3.5是所得6阶巴特沃斯滤波器的幅频与相频特性，所设计的通带满足指标要求，阻带指标略有富余，这样可以防止混叠带来的不良后果。

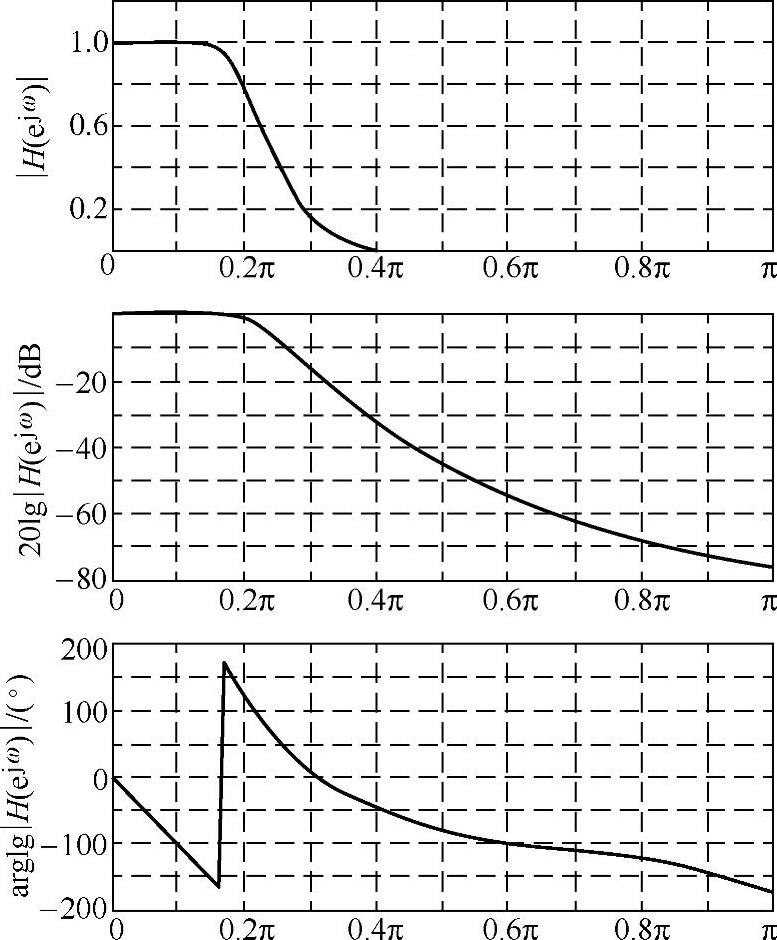
图5.3.5 用冲激响应不变法设计的6阶巴特沃斯滤波器特性

（2）用通带等波纹滤波器（切比雪夫滤波器）实现

首先确定由通带内起伏决定的参数ε。由切比雪夫滤波器特性，有

求得

ε=0.50885

再确定必需的阶数N，由切比雪夫滤波器特性式（5.2.13），有

由此得

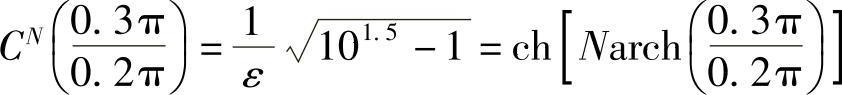
解得

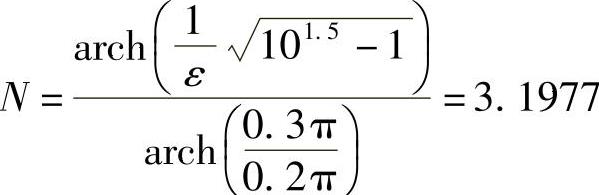
取N=4，可得椭圆参数为

短轴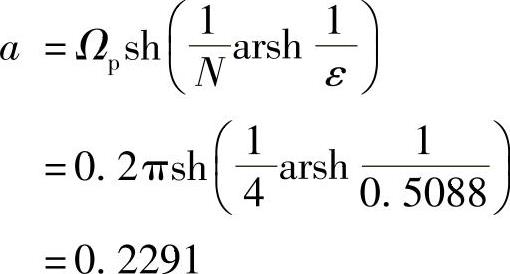

长轴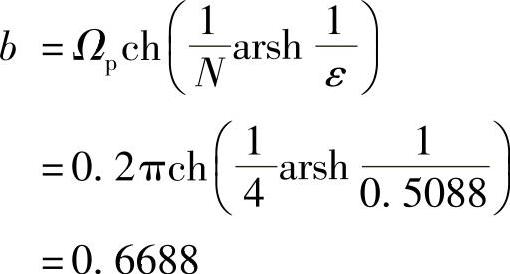

由此得到4个极点为

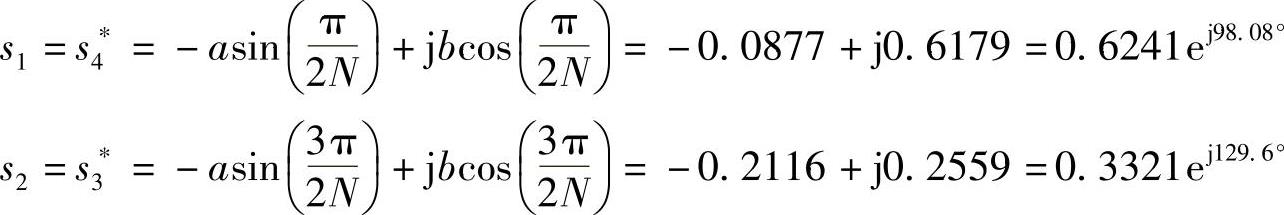
于是得到模拟滤波器的系统函数为

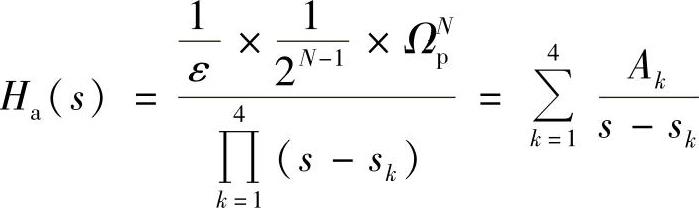
式中

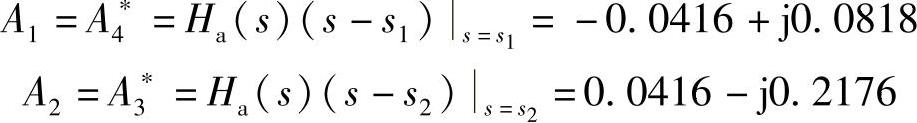
把式（5.2.13）的映射关系代入上式得

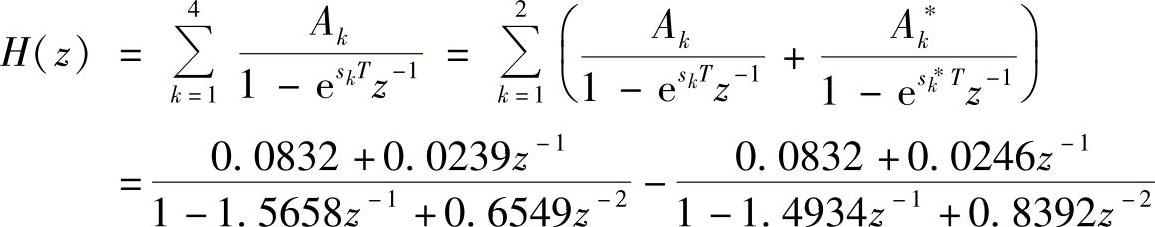
图5.3.6是所设计的切比雪夫滤波器的幅频和相频特性，由图可以看出，由于最后的阶数N=4比要求的N=3.1977高出较多，因而阻带的性能也相应地提高较多。

用冲激响应不变法得到的H（z），是以二阶环节相加的形式出现的，因而实现时可以用二阶子系统并联组合而成。

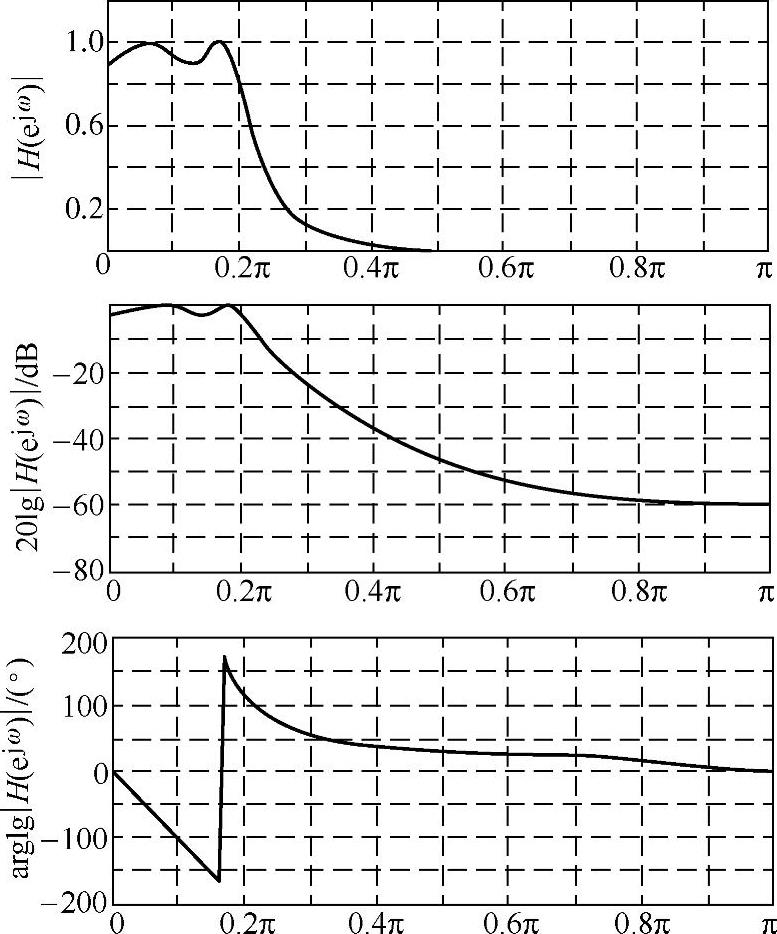
图5.3.6 用冲激响应不变法设计的4阶切比雪夫滤波器特性