模拟低通滤波器设计优化方案

设计模拟低通滤波器是根据一组规范来设计模拟系统函数H_a（s），使其逼近理想模拟低通滤波器的幅频特性，是根据幅度二次方函数来逼近的。也可根据其他指标来逼近，如相位响应特性或群延迟响应特性。由幅度二次方函数|H_a（jΩ|）²=H_a（jΩ）H^∗_a（jΩ），当h_a（t）为实数时，有

|H_a（jΩ）|²=H_a（jΩ）H_a（-jΩ） （5.2.1）

=H_a（s）H_a（s）|_s=jΩ

现在由已知的|H_a（jΩ）|²求H_a（s）。基本思路：将|H_a（jΩ）|²中的Ω转换为s，得到的函数中有多组零、极点。选取因果稳定的零、极点，构成H_a（s）。

1.巴特沃斯滤波器（最大平坦幅度特性滤波器）

巴特沃斯低通滤波器幅度平方函数定义为

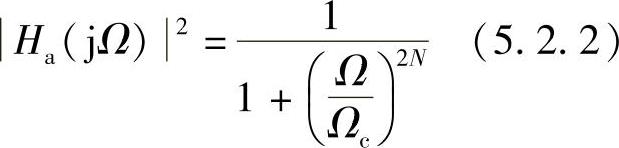
式中，N为滤波器的阶数。其幅频特性如图5.2.2所示，从图可以看出巴特沃斯低通滤波器幅频特性有如下特点：

1）|H_a（jΩ）|_Ω=0=1。

2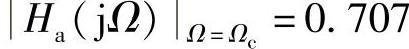），对于任何N都一样。即通带最大衰减为3dB，所有的曲线都经过该点，称为3dB不变性。当Ω＞Ω_c时，特性以20ndB/十倍频程速度下降，n是极点的数量。

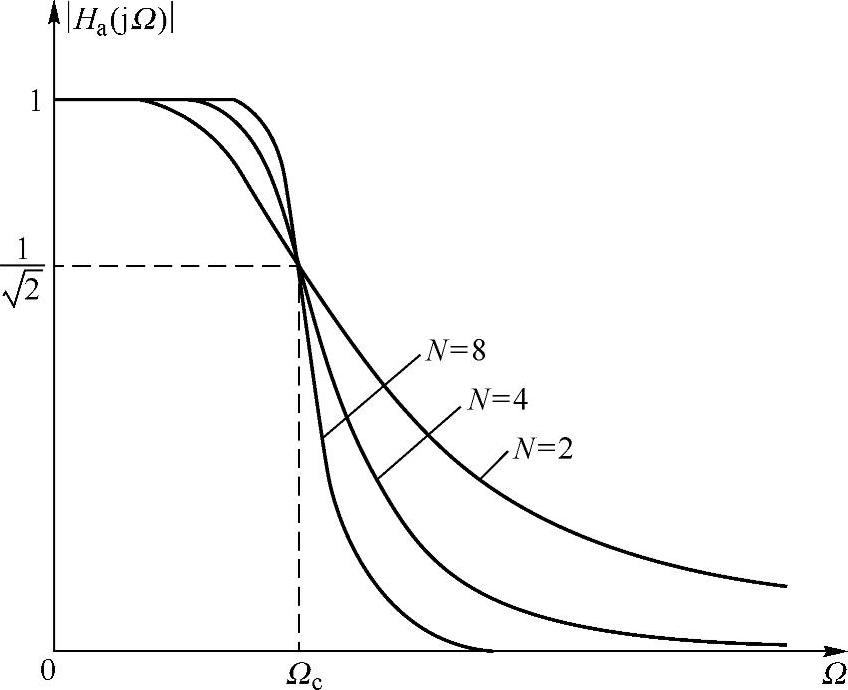
图5.2.2 巴特沃斯滤波器的幅频特性

3）巴特沃斯低通滤波器具有最大平坦性。对式（5.2.2）利用二项式定理展开成幂级数，即有

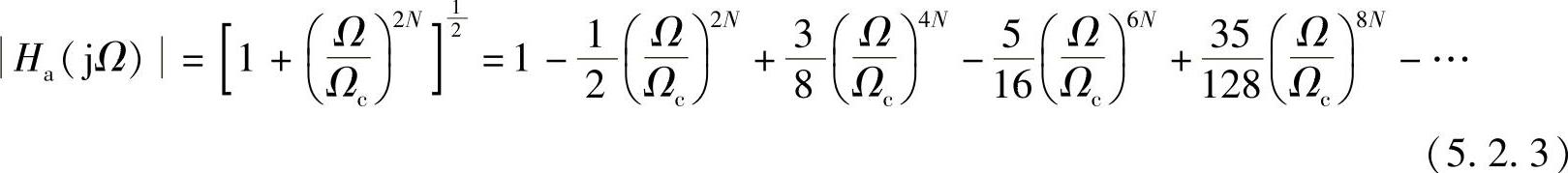
在Ω=0点，它的前2N-1阶导数都为零，这表示此函数在Ω=0点附近一段范围内“最平直”，可见巴特沃斯滤波器是以原点附近的最大平坦响应来逼近理想低通滤波器的。

下面由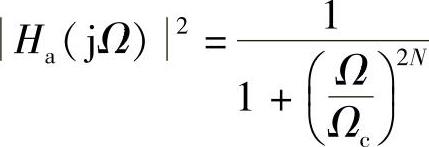求H_a（s）。

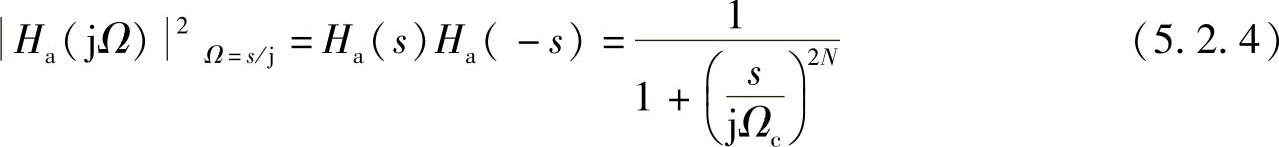
式中，在有限s平面只有极点而没有零点，称为“全极点型”滤波器。H_a（s）H_a（-s）的极点为

即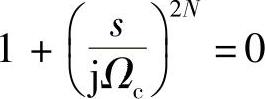

可得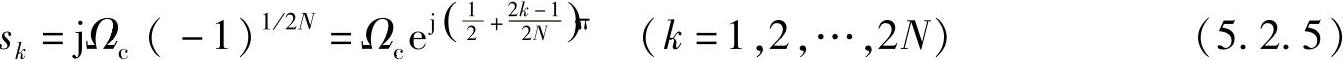

由式（5.2.5）极点值可以得出巴特沃斯滤波器极点分布的特点如下：

1）极点分布在半径为Ω_c的圆上，共有2N个极点。

2）极点间的角度间隔为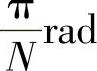，但第一个极点不一定是从0开始。

3）H_a（s）为稳定系统，则极点不能落在虚轴上。所以上式中的极点不能落在虚轴上。

4）判断在实轴上有无极点，只需看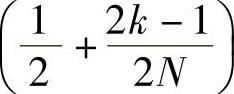π与mπ是否相等（m为整数）？也即判断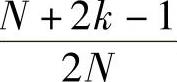是否等于m？（2k-1）始终为一个范围在1～（4N-1）内的奇数，2N为偶数。当N为奇数时，（N+2k-1）中存在2N的整数倍，这时实轴上有极点。当N为偶数时，（N+2k_-1）为奇数，这时实轴上没有极点。

图5.2.3画出了巴特沃斯滤波器系统函数的极点分布图。

H_a（s）H_a（-s）的左半平面的极点即为H_a（s）的极点，有N个，分别是

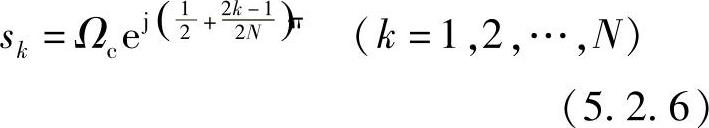
又因为|H_a（jΩ）|_Ω=0=1⇒H_a（s）|_s=jΩ=0=1，s=0时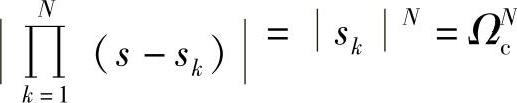，，由此，可得出

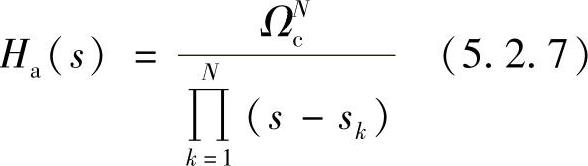
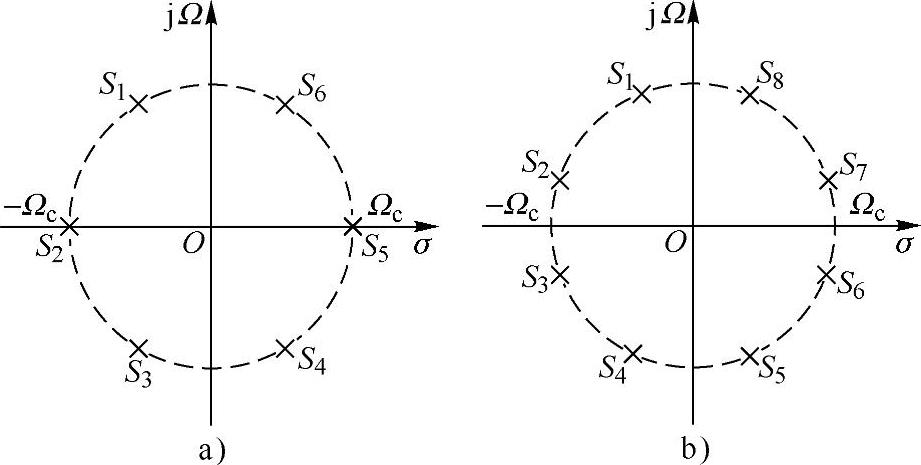
图5.2.3 巴特沃斯滤波器的极点分布

a）N=3 b）N=4

由于各滤波器的幅频特性不同，为使设计统一，将所有的频率归一化。采用对3dB截止频率Ω_c归一化，归一化后的H_a（s）表示为

令p=η+jλ=s/Ω_c，λ=Ω/Ω_c，λ称为归一化频率，p称为归一化复变量，这样，巴特沃斯滤波器的归一化低通原型系统函数为

式中，p_k=s_k/Ω_k为归一化极点，用下式表示为

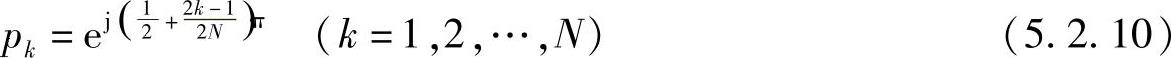
显然

s_k=Ω_cp_k （5.2.11）

这样，只要根据技术指标求出阶数N，然后按照式（5.2.10）求出N个极点，再按照式（5.2.9）得到归一化低通原型系统函数H_a（p）。如果给定Ω_c，再去归一化，即将p=s/Ω_c，s_k=Ω_cp_k代入H_a（p）中，便得到希望设计的系统函数H_a（s）。

将极点表示式（5.2.10）代入式（5.2.9），得到H_a（p）的分母是p的N阶多项式，用下式表示为

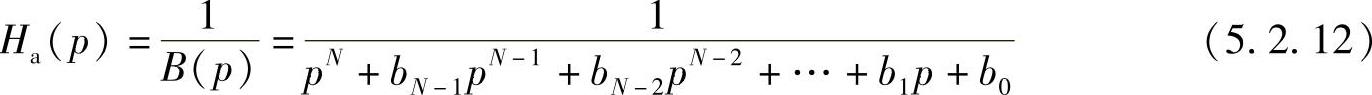
归一化原型系统函数H_a（p）的系数b_k（k=0，1，…，N-1），可由表5.2.1得到。另外，表5.2.2还给出了H_a（p）的因式分解形式中的各系数，这样只要求出阶数N，查表可得到H_a（s）及各极点，而且可以选择级联型和直接型结构的系统函数表示形式，避免了因式分解运算工作。

由式（5.2.6）和式（5.2.7）可知，只要求出巴特沃斯滤波器的阶数N和3dB截止频率Ω_c，就可以求出滤波器的系统函数H_a（s）。所以巴特沃斯滤波器的设计实质上就是根据设计指标求阶数N和3dB截止频率Ω_c的过程。下面通过两个实例介绍阶数N和Ω_c的求解过程。

【例5.2.1】 给定模拟滤波器技术指标为通带内允许起伏1dB，0≤Ω≤Ω_p=2π×10⁴rad/s；阻带内衰减≤15dB，Ω_s=2π×1.5×10⁴rad/s。用巴特沃斯滤波器实现时，求出阶数N、截止频率Ω_c和H_a（s）。

解 1）求N。由式（5.1.8）和式（5.1.9）可得

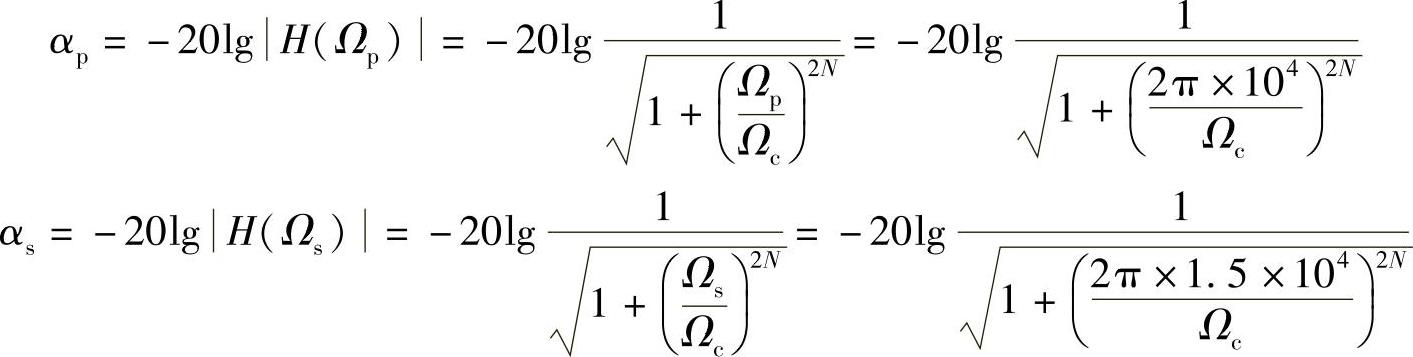
即

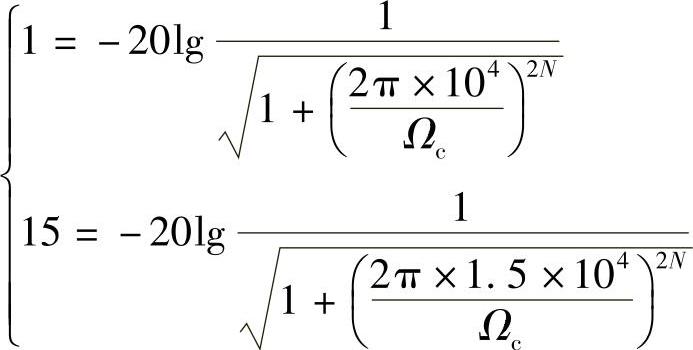
解上述联立方程可得

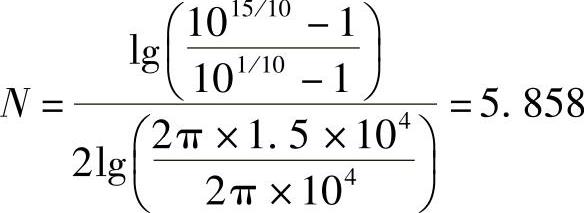
取N=6。

2）求Ω_c。让阻带满足指标要求，这样通带指标有富余（如果让通带指标满足要求，则阻带指标有富余）。由

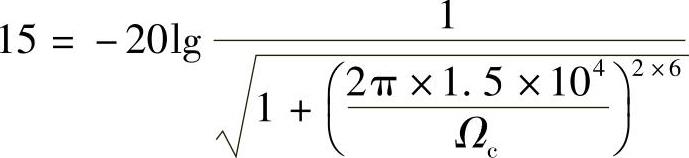
得。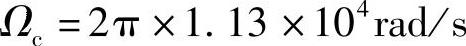

图5.2.4 6阶巴特沃斯 滤波器的极点分布

3）求极点分布。由于N=6，因而H_a（s）的极点分布如图5.2.4所示，对应的极点为

s₁=s^∗₆=2π×1.13×10⁴e^j105°

s₂=s^∗₅=2π×1.13×10⁴ej135°

s₃=s^∗₄=2π×1.13×10⁴e^j165°

4）求滤波器的系统函数H_a（s），有

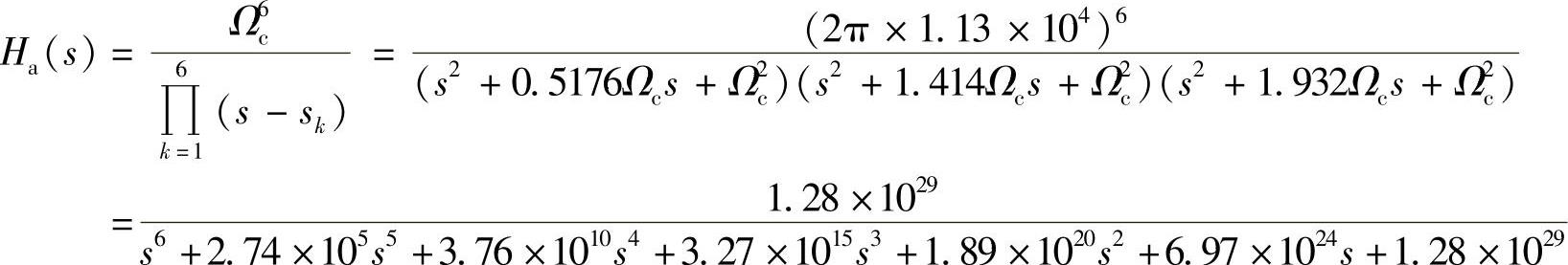
【例5.2.2】 设计一个巴特沃斯低通滤波器，要求通带截止频率f_p=6kHz，通带最大衰减a_p=3dB，阻带截止频率f_s=12kHz，阻带最小衰减α_s=25dB。求出滤波器归一化系统函数H_a（p）以及实际的H_a（s）。

解 1）求阶数N。由式（5.1.8）和式（5.1.9）可得

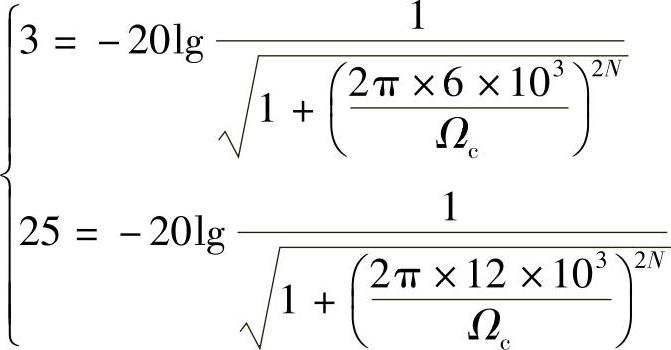
解上述联立方程可得

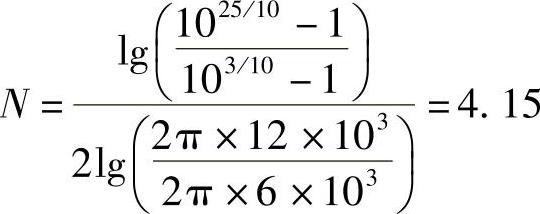
所以取N=5（实际应用中，根据具体要求，也可能取N=4，指标稍微差一点，但阶数低一阶，使系统实现电路得到简化）。

2）求归一化系统函数H_a（p）。由阶数N=5直接查表5.2.1或表5.2.2得到5阶巴特沃斯归一化低通滤波器系统函数H_a（p）为

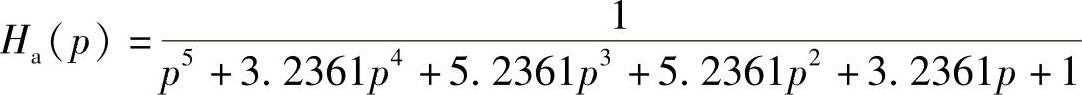
或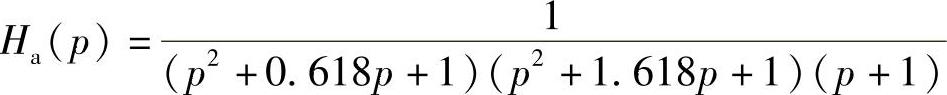

当然，也可以按式（5.1.10）计算出极点为

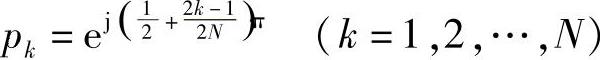
则H_a（p）表达式为

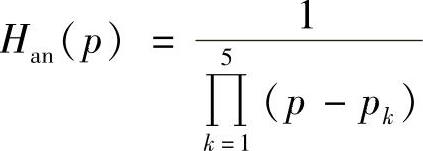
代入p_k值并进行分母展开得到与查表相同的结果。

3）去归一化。由归一化系统函数H_a（p）得到实际滤波器系统函数H_a（s）。由于本题中a_p=3dB，即Ω_c=Ω_p=2π×6×10³rad/s，因此

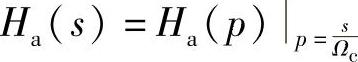
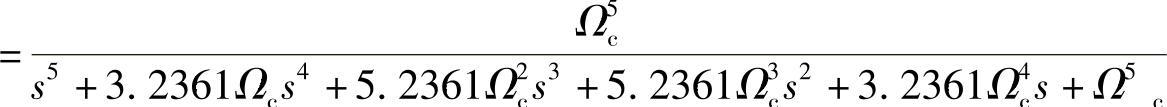
对分母的因式形式，则有

如以上结果中，Ω_c的值未代入相乘，这样使读者能清楚地看到去归一化后，3dB截止频率对归一化系统函数的改变作用。

表5.2.1 巴特沃斯多项式表

表5.2.2 巴特沃斯因式表

2.切比雪夫Ⅰ型滤波器（通带等波纹滤波器）

巴特沃斯低通滤波器的幅频特性，无论在通带与阻带内都随频率而单调变化，滤波特性简单。在通带内误差分布不均匀，靠近频带边缘误差最大，当滤波器阶数n较小时，阻带幅频特性下降较慢，与理想滤波器的特性相差较远。若要求阻带特性下降迅速，则需增加滤波器的阶数，这样设计该滤波器时所用元器件数量就会增多，电路也趋于复杂。

若将误差均匀地分布在通带内，就可以设计出阶数较低的滤波器。这种误差均匀分布的办法可通过选择具有等波纹特性的逼近函数来完成。切比雪夫滤波器就可以做到这一点。

切比雪夫滤波器是由切比雪夫多项式的正交函数推导出来的，采用了在通带内等波动，在通带外衰耗单调递增的准则去逼近理想滤波器特性。切比雪夫滤波器有两种形式：其频率响应的幅度在通带内是等波纹的，在阻带内则是单调下降的，称为切比雪夫Ⅰ型滤波器；在通带内是单调的，在阻带内是等波纹的，称为切比雪夫Ⅱ型滤波器。采用何种形式的切比雪夫滤波器取决于实际用途。在此仅介绍切比雪夫Ⅰ型滤波器的设计方法。其幅度二次方函数表示为

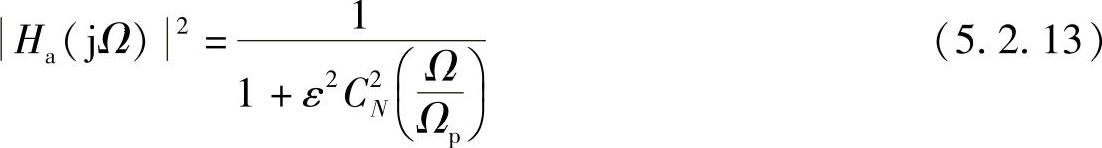
式中，ε是决定通带内起伏大小的系数，ε＜1；C_N（x）为N阶切比雪夫多项式，它的特性为

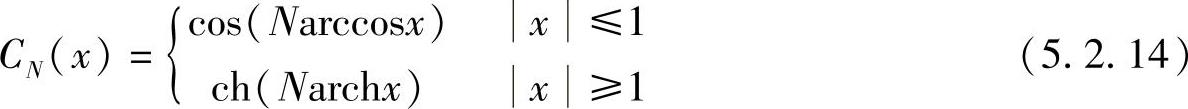
切比雪夫多项式的性质如下：

1）递推关系为

C_N+1（x）=2xC_N（x）-C_N-1（x） （N=1，2，…） （5.2.15）

于是有

C₀（x）=1

C₁（x）=x

C₂（x）=2x²-1

C₃（x）=4x³-3x

C₄（x）=8x⁴-8x²+1

C₅（x）=16x⁵-20x³+5x

C₆（x）=32x⁶-48x⁴+18x²-1

…

证明 显然，N=0时，C₀（x）=1；N=1时，C₁（x）=x。当n≥1时，令x=cosθ，则C_N（x）=cosNθ。由三角恒等式

cos（N+1）θ+cos（N-1）θ=2cosNθcosθ

即得

C_N+1（x）+C_N-1（x）=2xC_N（x）

移项就得上述递推关系式（5.2.15）。

2）切比雪夫多项式{C_N（x）}在区间[-1，1]上带权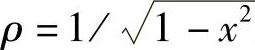正交，且

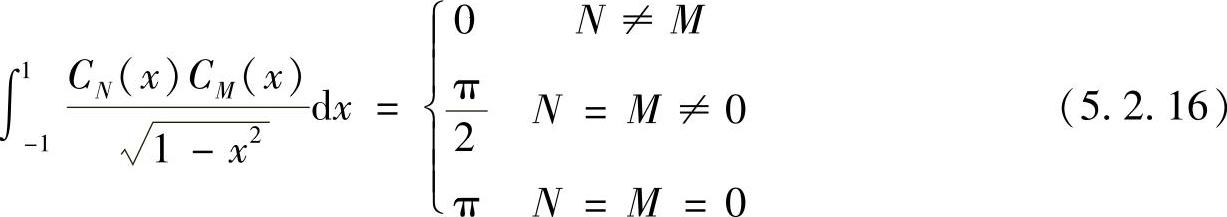
证明 因为C_N（x）=cos（Narccosx），令x=cosθ，则C_N（x）=cosNθ，于是

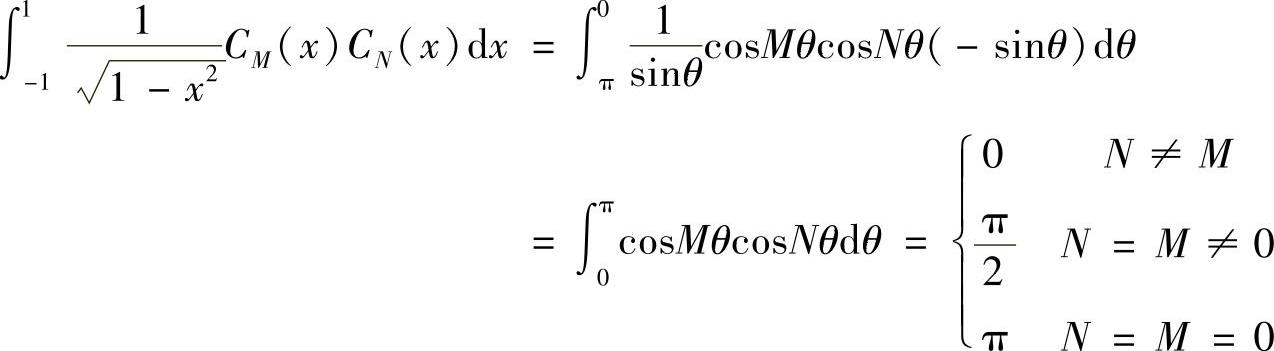
3）C_N（x）的奇偶性决定于N是奇数还是偶数，即

C_N（-x）=C_N（x） （N=偶数） （5.2.17a）

C_N（-x）=-C_N（x） （N=奇数） （5.2.17b）

证明

C_N（-x）=cos[Narccos（-x）]=cos（Nπ-Narc cosx）

=（-1）^Ncos（Narccosx）=（-1）^NC_N（x）

4）C_2k（x）只含x的偶次幂，C_2k+1（x）只含x的奇次幂。

5）C_N（x）在区间[-1，1]上有N个不同的零点

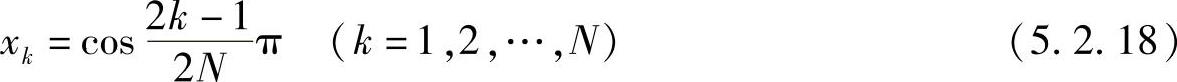
证明 由于C_N（x）=cosNθ，令C_N（x）=0，则有

Nθ=kπ-π/2 （k=1，2，…，N）

所以在区间0≤θ≤π上有N个值

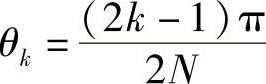
使cosNθ_k=0

即cosNθ在[0，π]中有N个不同的零点，且由于C_N（x）是N次多项式，所以至多有N个零点，现已找到N个不同的零点，则每一个x_k都是C_N（x）的单重零点。

显然，C_N（x）在[-1，1]中的零点都是实的、互异的，且全部在[-1，1]内。

6）若将xⁿ用C₀（x），C₁（x），…，C_n（x）的线性组合表示，则其公式为

7）C_N（x）在[-1，1]上有N+1个不同的极值点

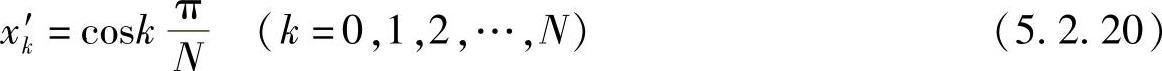
使C_N（x）轮流取得最大值1和最小值-1。

证明 因为在区间0≤θ≤π上有N+1个点

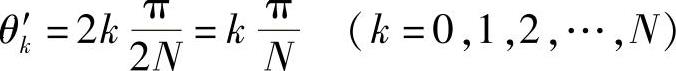
使cosNθ顺次取1及-1，因此，N+1个点

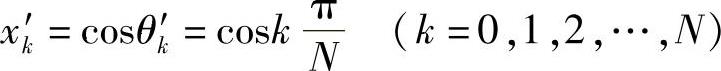
使C_N（x）顺次为1及-1，即

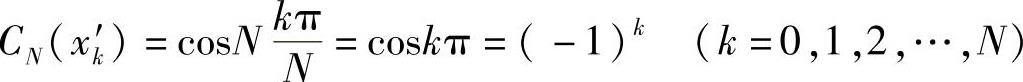
由于cosNθ之最大值是1，最小值是-1，因此，把这N+1个点x′_k叫做C_N（x）在[-1，1]上的极值点，也称它为C_N（x）的交错点组。如果将C_N（x）的零点x_k和极值点x′_k按大小排列，则有

-1=x_N′＜x_N＜x′_N-1＜x_N-1＜…＜x₁′＜x₁＜x′₀=1

8）C_N（x）的最高次项系数为2^N-1。

9）当x＜1时，C_N（x）≤1，且具有等波纹特性；当x＞1时，C_N（x）随x单调上升。

10）图5.2.5画出了C₁（x）～C₄（x）的曲线，从这组曲线可以看出，x=0，1或-1时，N不论为何值都有

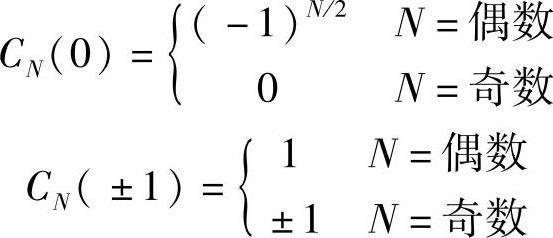(www.xing528.com)

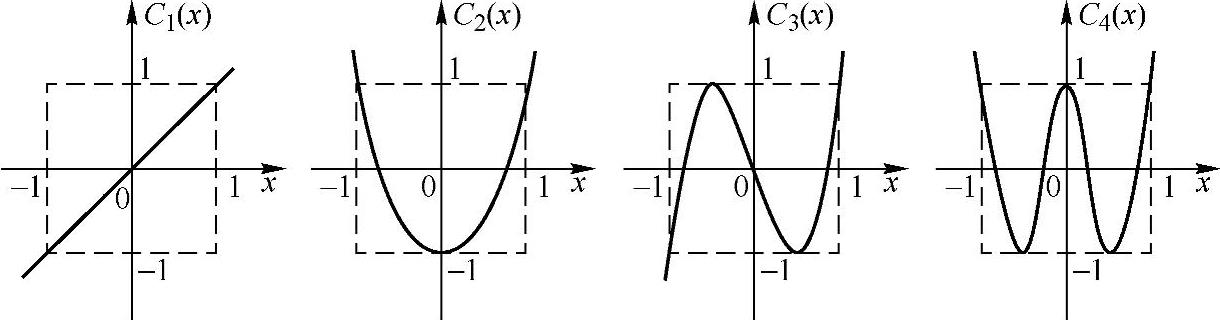
图5.2.5 C₁（x）～C₄（x）的特性曲线

对应式（5.2.13）的切比雪夫滤波器的幅频特性如图5.2.6所示。图5.2.7是切比雪夫多项式与其对应的滤波特性起伏波纹间的关系。当C₅（x）在±1之间波动时，|H_a（jp）|在通带内起伏在1和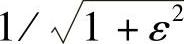之间变化，但两者的周期并不相等。当N为奇数时，H_a（j0）=1；当N为偶数时，。

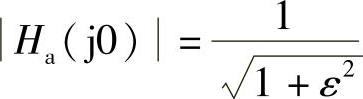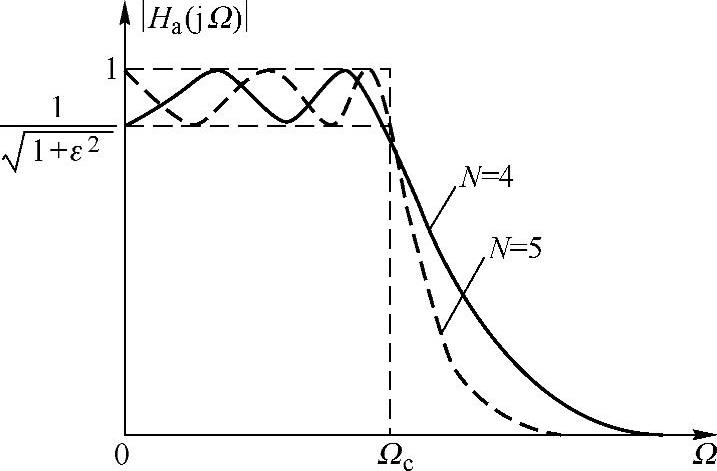
图5.2.6 切比雪夫滤波器的幅频特性

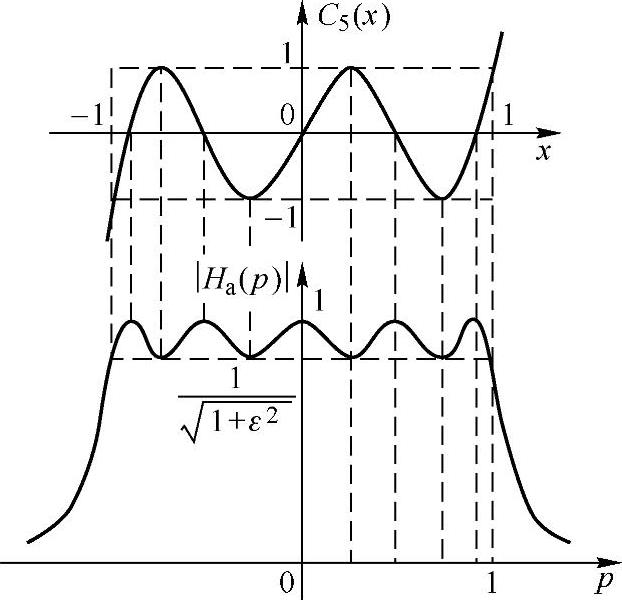
图5.2.7 C₅（x）与带内波纹之间的关系

为了比较巴特沃斯滤波器和切比雪夫Ⅰ型滤波器的性能，图5.2.8分别画出了四阶切比雪夫Ⅰ型和巴特沃斯低通滤波器的幅频特性，从图可以看出巴特沃斯滤波器的幅频特性在通带内随着Ω的增加与理想特性的偏离增大，误差分布是不均匀的。而切比雪夫Ⅰ型滤波器特性在通带内误差分布是均匀的。实际上切比雪夫Ⅰ型滤波器是在通带内幅频特性以最大误差最小化对理想低通滤波器特性的最佳一致逼近，因而通带内幅频特性呈现等波纹变化。

切比雪夫Ⅰ型滤波器有三个参数需要确定：波动系数ε，通带截止频率ω_p和阶数N。通带截止频率一般按照实际要求给定；ε表示通带内最大损耗，由容许的通带最大衰减α_p确定。

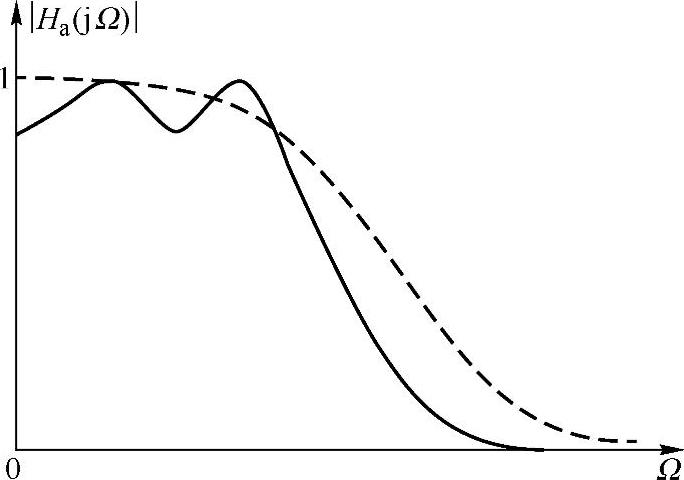
图5.2.8 四阶切比雪夫Ⅰ型（实线）和巴特沃斯（虚线）低通滤波器的幅频特性比较

（1）确定ε

应用式（5.1.8），则有

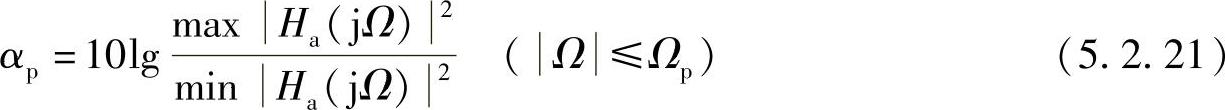
式（5.2.21）中

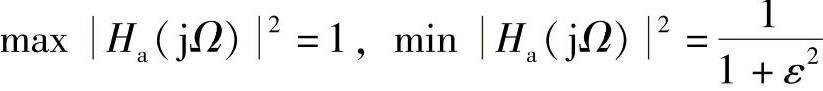
因此

α_p=10lg（1+ε²） （5.2.22）

由式（5.2.22）可得

（2）确定N

阶数N影响过渡带的宽度，同时也影响通带内波动的疏密，因为通带内有N+1个极值点。设阻带的起始点频率（阻带截止频率）用Ω_s表示，在Ω_s处的|H_a（jΩ）|²用式（5.2.13）确定

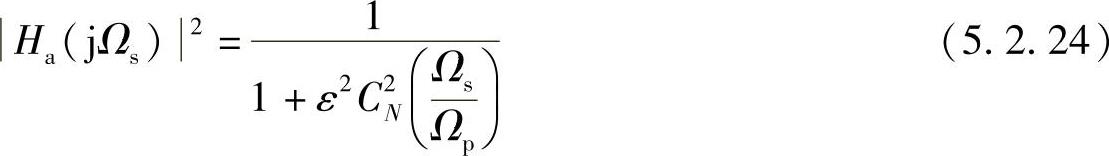
令λ_s=Ω_s/Ω_p，由λ_s＞1，有

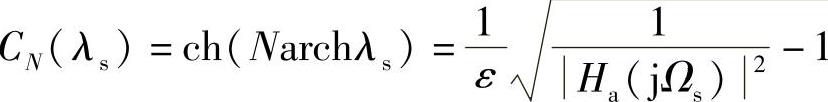
可以求得

（3）确定3dB截止频率Ωc

通带截止频率Ω_p通常由设计指标给出，根据3dB截止频率的定义，有

将式（5.2.26）代入式（5.2.13），有

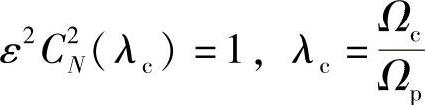
通常λ_c＞1，因此

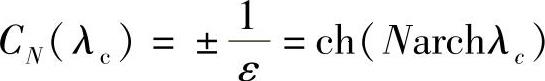
上式取正号，得

上述三个参数确定后，就可以求出滤波器的极点，并确定归一化系统函数H_a（p），p=s/Ω_p。

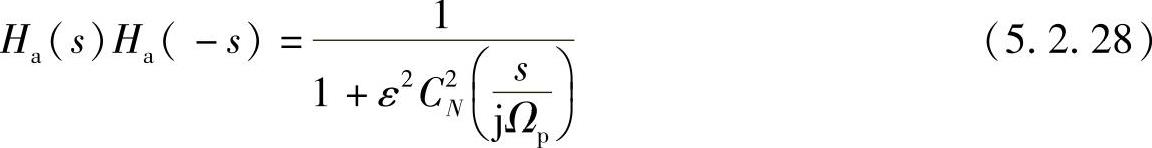
令分母多项式等于零，有

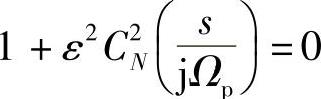
所以有

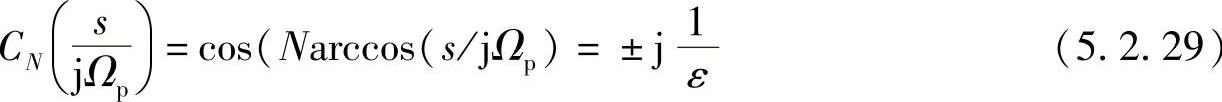
令

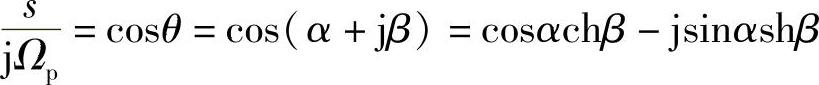
则有

s=Ω_psinαshβ+jΩ_pcosαchβ=σ+jΩ （5.2.30）

为了求α，β与ε的关系，将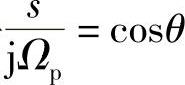代入式（5.2.29），得

由此得出

解上述联立方程，得

cos（Nα）=0

即

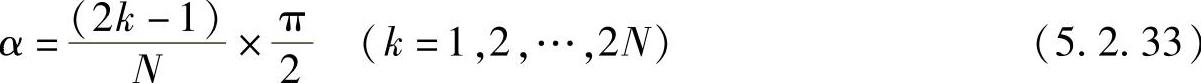
把α的值代入式（5.2.32）中的第二个方程，得

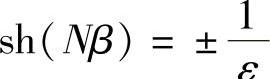
即

把α和β的值代入式（5.2.30），得出极点为

即

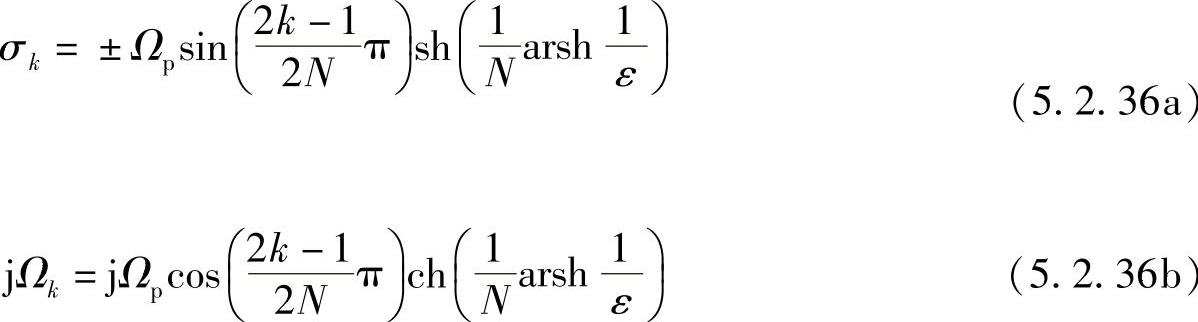
从式（5.2.36a）和式（5.2.36b）可得

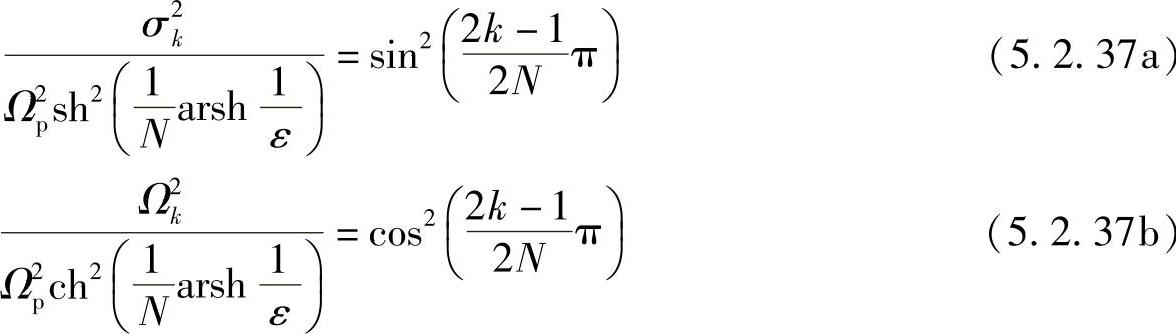
式（5.2.37a）和（5.2.37b）两式相加得极点s_k在s平面上的分布满足如下方程，即

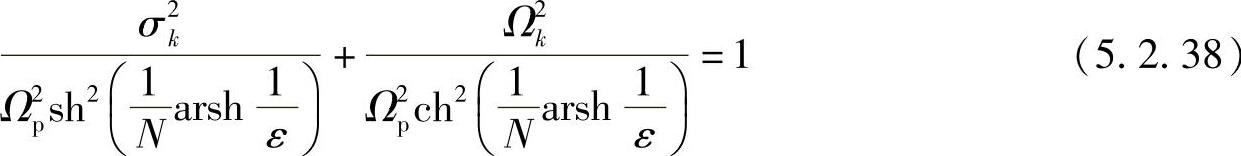
式（5.2.38）是一个椭圆方程，其短轴a和长轴b分别为

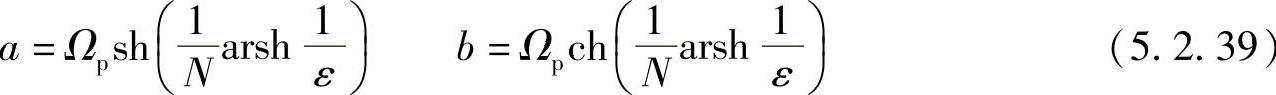
图5.2.9画出了N=3和N=4时的极点分布。如果取左半平面的极点构成H_a（s），即

其中极点s_k的实部和虚部分别为

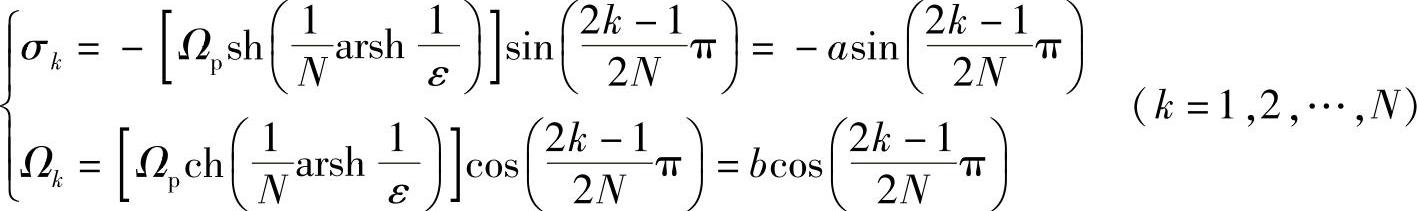
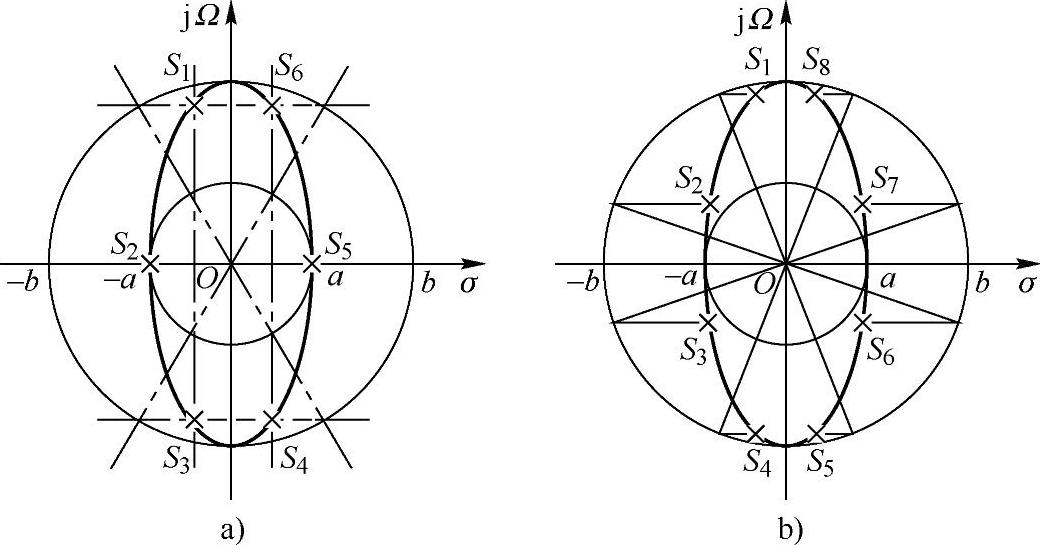
图5.2.9 切比雪夫滤波器的极点分布

a）N=3 b）N=4

增益常数A用如下方法确定，将Ω=s/j代入式（5.2.13）得

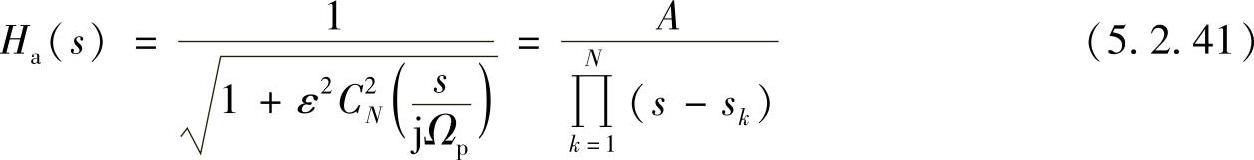
式（5.2.41）第二个等号右端分母展开后是s的多项式，其最高阶次系数是1，又考虑到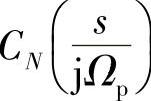为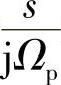的多项式，且由切比雪夫多项式的性质8）可知，最高阶前面系数是2^N-1，因而式（5.2.41）中常数A为

这样切比雪夫Ⅰ型滤波器的系统函数为

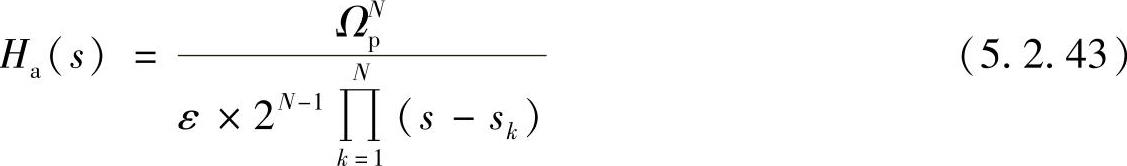
将复频域s归一化，即s=pΩ_p，即得归一化系统函数H_a（p）为

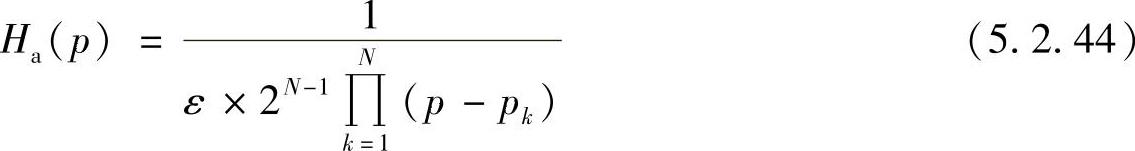
由上面的讨论可知：切比雪夫滤波器的极点分布特征与巴特沃斯滤波器的极点分布是相同的，其中大小两个圆就是巴特沃斯分布的圆。切比雪夫滤波器极点的纵坐标Ω_k由大圆的等分角连线决定，极点的横坐标σ_k由小圆的等分角连线决定。

【例5.2.3】 给定模拟滤波器的技术指标为

通带内允许起伏1dB，0≤Ω≤Ω_p=2π×10⁴rad/s；阻带内衰减≤15dB，Ω_s=2π×1.5×10⁴rad/s。用切比雪夫Ⅰ型滤波器实现时，求出阶数N和H_a（s）表示式。

解 （1）求带内起伏参数ε由滤波器的滤波特性知道，带内起伏ε满足

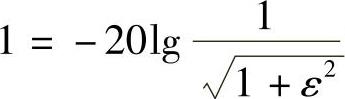
求得

ε=0.5088

（2）求阶数N

由给定的阻带指标得

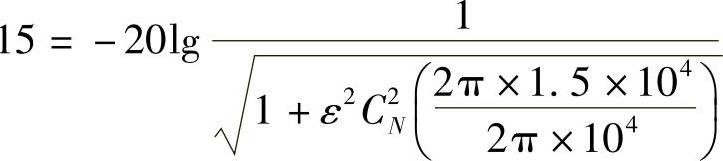
解得

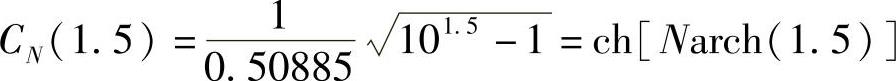
由此得

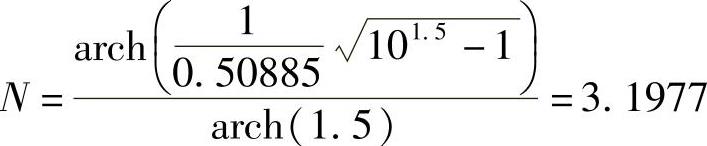
取N=4，它的极点分布如图5.2.9b所示，其椭圆的短轴a与长轴b分别为

（3）求极点分布

由图5.2.9b及式（5.2.35）可以得到

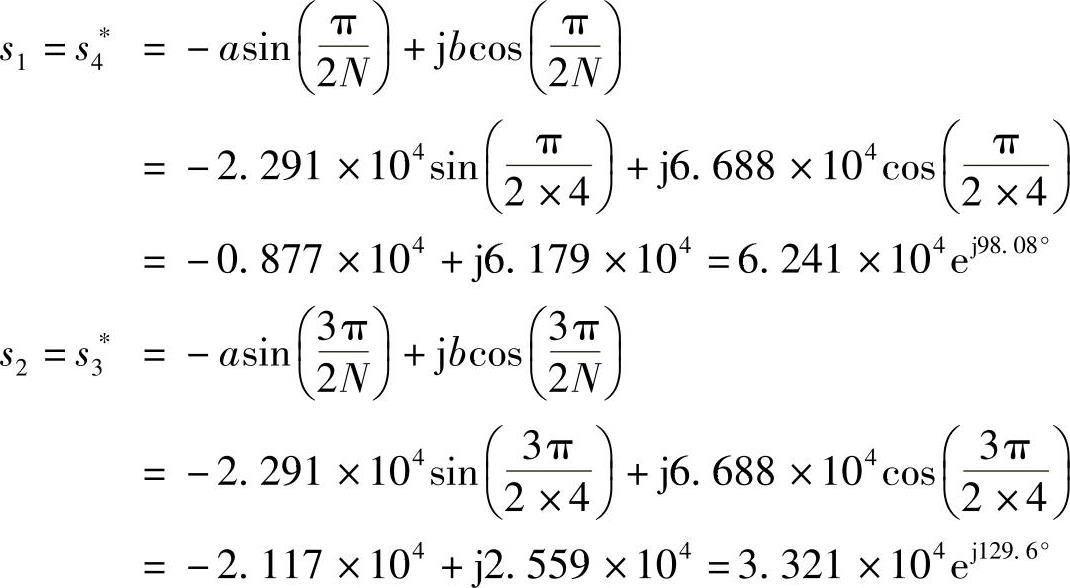
（4）求滤波器的系统函数H_a（s）

由式（5.2.43）得

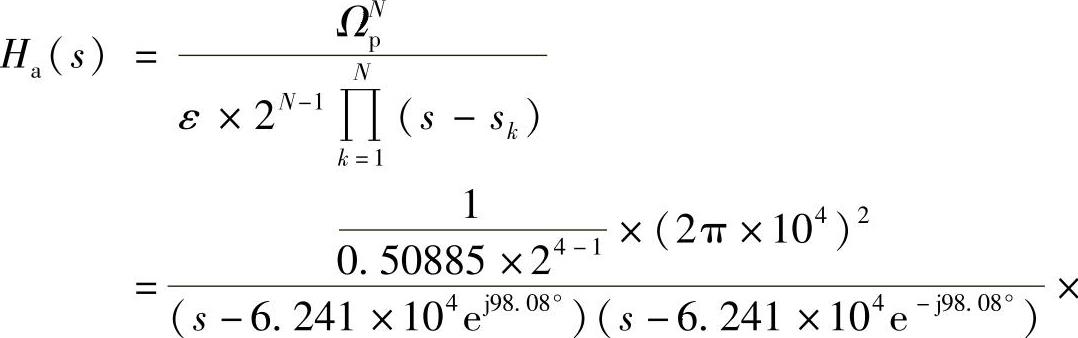
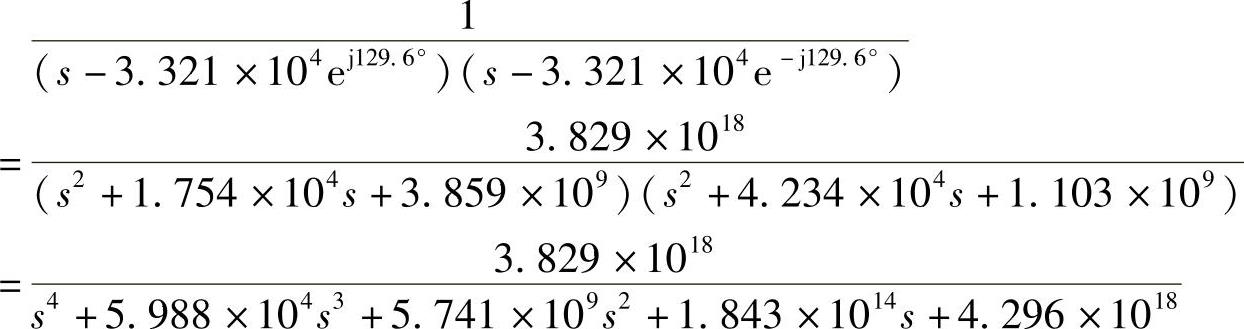
从这个例子可以看出，对同样的指标要求，切比雪夫滤波器所需要的阶数比巴特沃斯滤波器低，因而结构简单。其缺点是通带内等波纹起伏，使其相位的非线性失真比巴特沃斯滤波器的大，这在某些使用场合应尽量避免。

3.其他滤波器

（1）切比雪夫Ⅱ型低通滤波器

切比雪夫Ⅱ型低通滤波器可以通过一种变换与切比雪夫Ⅰ型低通滤波器联系起来。具体来讲，把式（5.2.13）中的ε²C²_N（Ω/Ω_c）项用其倒数来替换，并且把C²_N的自变量也用其倒数来代替，则可以得到

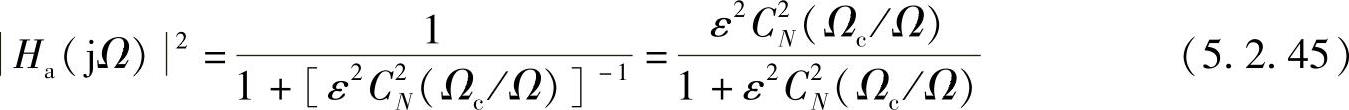
式（5.2.45）就是切比雪夫Ⅱ型低通滤波器的幅度二次方特性。设计切比雪夫Ⅱ型低通滤波器的一种方法是：首先设计切比雪夫Ⅰ型低通滤波器，然后再利用上述的变换即可。其幅频特性如图5.2.10所示。

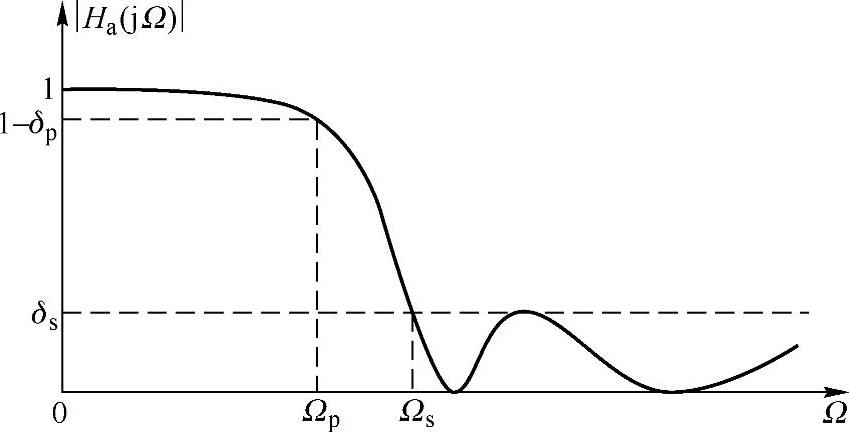
图5.2.10 切比雪夫Ⅱ型低通滤波器的幅频特性

（2）椭圆滤波器（考尔滤波器）

如果像在切比雪夫滤波器的情况中那样，使误差均匀分布于整个通带或整个阻带，而不是像巴特沃斯滤波器那样，只允许误差在通带内单调地增加。那么就可以用一个较低阶数的滤波器满足设计要求。在切比雪夫Ⅰ型低通滤波器逼近和巴特沃斯逼近中，阻带误差随频率单调减小，如果是阻带误差均匀地分布于阻带内，就有导致进一步改进的可能性。这样就可以提出一种低通滤波器的逼近方法，即在通带内和阻带内均等波纹，这种逼近称为椭圆滤波器，它的幅度平方函数为

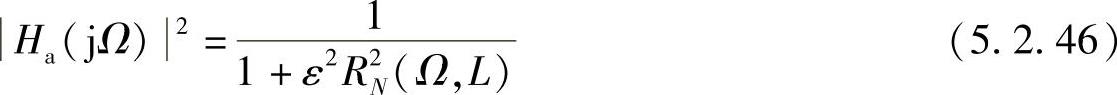
式中，R_N（Ω，L）为雅克比椭圆函数，L是一个表示波纹性质的参量。图5.2.11画出了N=5时，R²₅（Ω，L）的特性曲线。图5.2.12画出了椭圆滤波器的幅度二次方函数，该滤波器有这样的特点：幅频响应在通带和阻带内都是等波纹的，椭圆滤波器既有极点又有零点，对于给定阶数和给定的波纹要求，椭圆滤波器能够获得较其他滤波器为窄的过渡带宽。

从图5.2.11可以看出，在归一化通带内（-1≤Ω≤1），在0和1间振荡，而超过Ω_L后，在L²和∞间振荡。L越大，Ω_L也变大。这一特点使滤波器同时在通带和阻带具有任意衰减量。

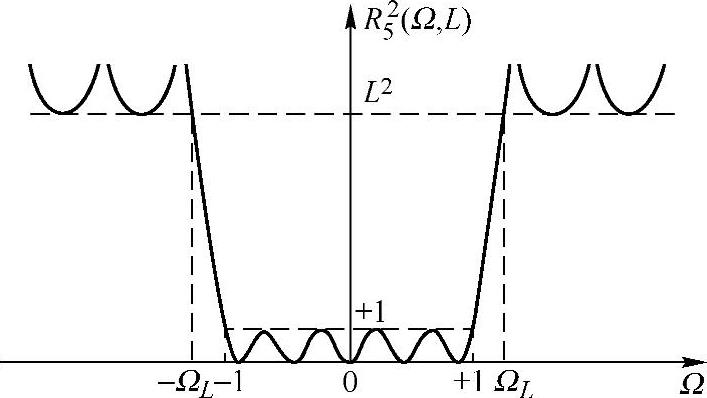
图5.2.11 R²₅（Ω，L）特性曲线

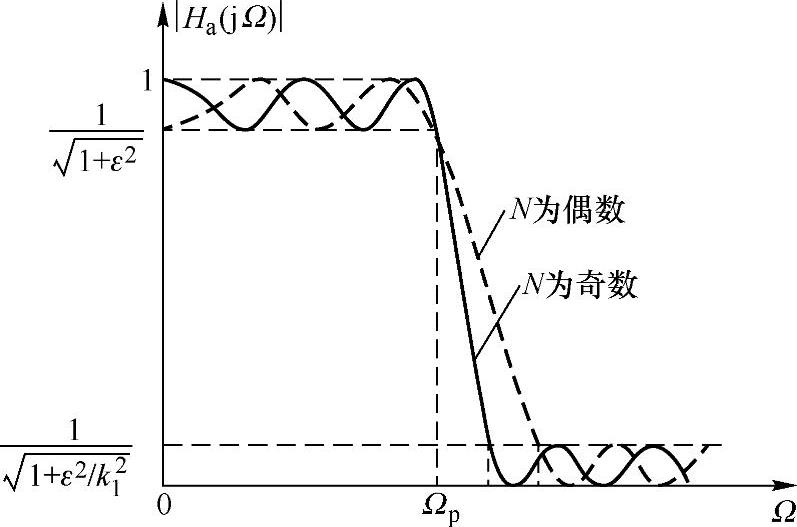
图5.2.12 椭圆滤波器的幅频特性

ε的定义与切比雪夫滤波器相同。当Ω_p、Ω_s、ε确定之后，阶次N的确定方法为

式中

k=Ω_p/Ω_s

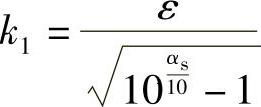
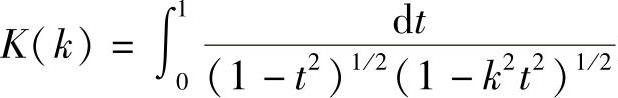为第一类完全的椭圆积分。

前面讨论了三种常用的模拟低通滤波器的特性和设计方法，设计时应按照指标要求，合理选用。一般椭圆滤波器的阶次可最低，切比雪夫次之，巴特沃斯最高。参数的灵敏度则恰恰相反。

（3）贝塞尔滤波器

电子学和信号处理中，贝塞尔（Bessel）滤波器是具有最大平坦群延迟（线性相位响应）的线性滤波器。贝塞尔滤波器常用在音频天桥系统中。模拟贝塞尔滤波器描绘为几乎横跨整个通频带的恒定的群延迟，因而在通频带上保持了被过滤的信号波形。

贝塞尔滤波器具有最平坦的幅度和相位响应。带通（通常为用户关注区域）的相位响应近乎呈线性。贝塞尔滤波器可用于减少所有无限冲激响应滤波器固有的非线性相位失真。

虽然贝塞尔滤波器在它的通频带内提供平坦的幅度和线性相位（即一致的群延时）响应，但它的选择性比同阶的巴特沃斯滤波器或切比雪夫滤波器要差。因此，为了达到特定的阻带衰减水平，需要设计更高阶的贝塞尔滤波器。

贝塞尔滤波器的系统函数可表示为

式中，B_N（s）为N阶贝塞尔函数；B_N（0）是多项式在s=0时的值。贝塞尔多项式有如下递推公式

B_N（s）=（2N-1）B_N-1（s）+s²B_N-2（s） （5.2.49）

于是有

B₀（s）=1

B₁（s）=s+1

B₂（s）=s²+3s+3

B₃（s）=s³+6s²+15s+15

B₄（s）=s⁴+10s³+45s²105s+105

B₅（s）=s⁵+15s⁴+105s³+420s²+945s+945

…

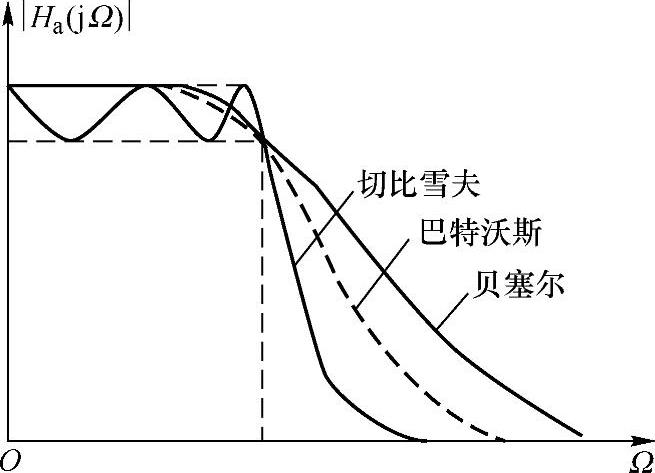
图5.2.13 三种滤波器幅频特性的比较

将式（5.2.48）中的s用jΩ代替，即得到频率响应特性。图5.2.13画出了巴特沃斯、切比雪夫、贝塞尔三种滤波器的幅度特性曲线。由图可以看出，切比雪夫滤波器的幅频特性曲线边沿下降陡峭，但顶部不平坦；贝塞尔滤波器的顶部少起伏但边沿下降缓慢；巴特沃斯滤波器特性介于二者之间。