数字滤波器的分类及特点分析

1.一般分类

经典滤波器：输入信号中的有用的频率成分和希望滤除的频率成分占用不同的频带，通过选频滤波器达到滤波的目的。

现代滤波器：信号和干扰的频带相互重叠，要利用信号的统计分布规律，从干扰中最佳提取信号，如维纳滤波器、卡尔曼滤波器和自适应滤波器等。

2.从滤波器的功能上来分类

分为低通、高通、带通、带阻滤波器。各种理想滤波器的幅度特性如图5.1.1所示。

图5.1.1 理想低通、高通、带通和带阻滤波器的幅度特性

a）低通 b）高通 c）带通 d）带阻

特点：①单位抽样响应是非因果且无限长，不可能实现，只能尽可能逼近。②数字滤波器的系统函数是以2π为周期，低通的中心频带处于2π的整数倍处，高通的中心频带处于π的奇数倍附近。在数字滤波器中，一般考察其半个周期ω=[0，π]的频域特性；在模拟滤波器中，通常考察其Ω=[0，∞]范围内频率域的特性。(www.xing528.com)

3.按时间域特性分类

可以分为无限冲激响应数字滤波器（IIR滤波器）和有限冲激响应数字滤波器（FIR滤波器）两类。

无限冲激响应滤波器的系统函数为

h[n]为滤波器的脉冲响应，n=0～∞均有值。M和N为分解的分子和分母多项式的系数个数。有限冲激响应滤波器的系统函数为

该滤波器的单位抽样响应h[n]在n=0，1，…，N-1的有限个点（N个点）上有值。注意式（5.1.4）中分母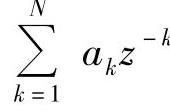全为零时，H（z）具有全零点形式，无限冲激响应滤波器退化为有限冲激响应滤波器。