频率抽样结构在有限冲激响应系统中的应用

在第2章中已讲过，把一个有限长序列（长度为N点）的z变换H（z）在单位圆上作N等分抽样，就得到H[k]，其主值序列就等于h[n]的离散傅里叶变换H[k]。设

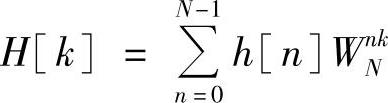
则有

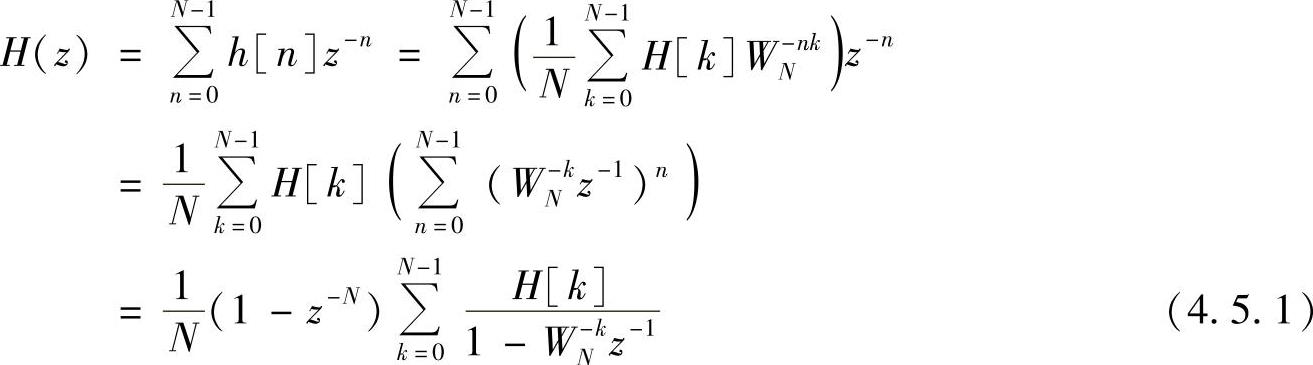
式（4.5.1）就是对有限冲激响应系统给定单位圆上的取样值H[k]，利用内插关系得到的H（z）。由于这种结构是通过频率取样得到的，存在时域混叠的问题，因而不适合无限冲激响应系统，只适合有限冲激响应系统。这种结构由两部分级联组成：

级联的第一部分为

H_c（z）=1-z^-N （4.5.2）

这是一个有限冲激响应子系统，是由N节延时单元构成的梳状滤波器，令

H_c（z）=1-z^-N=0

则有

z^N_i=1=ej2πi

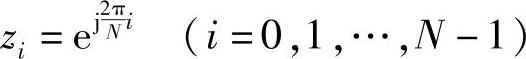
即H_c（z）在单位圆上有N个等间隔角度的零点，它的频率响应为

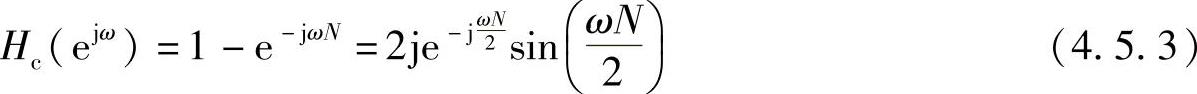
因而幅频特性为

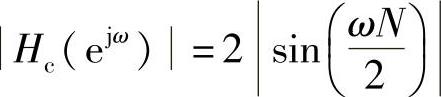
辐角为

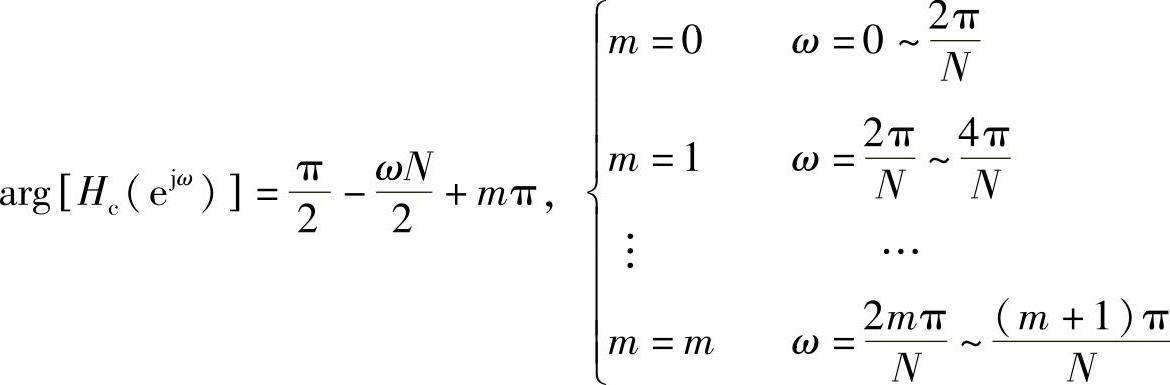
其子系统结构及幅度频率响应分别如图4.5.1和图4.5.2所示。

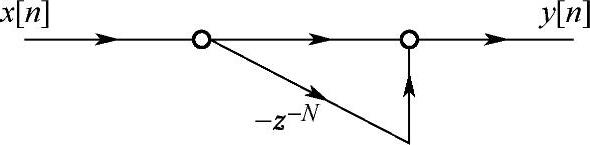
图4.5.1 梳状滤波器结构流图

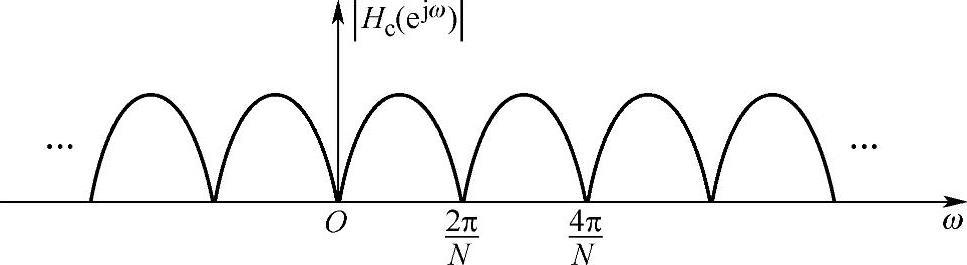
图4.5.2 梳状滤波器的幅度频率响应

级联的第二部分为

它是由N个一阶系统并联组成，而这每一个一阶系统都是一个谐振器

令H′（z）的分母为零，即

1-W_N^-kz^-1=0

可得到此一阶系统在单位圆上有极点，。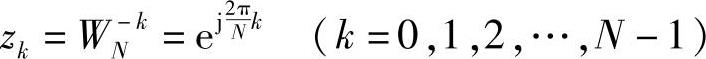

也就是说，此一阶系统在频率为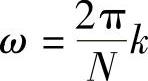处响应为无穷大，故等效于谐振频率为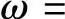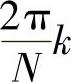的无损耗谐振器。这个谐振器的极点正好与梳状滤波器的一个零点（i=k）相抵消，从而使这个频率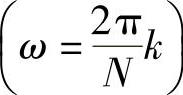上的频率响应等于H[k]。这样，N个谐振器的N个极点就和梳状滤波器的N个零点相互抵消，从而在N个频率抽样点上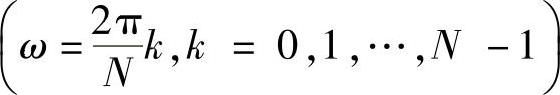的频率响应就分别等于N个H[k]值。(www.xing528.com)

N个并联谐振器与梳状滤波器级联后，就得到图4.5.3所示的频率抽样结构。

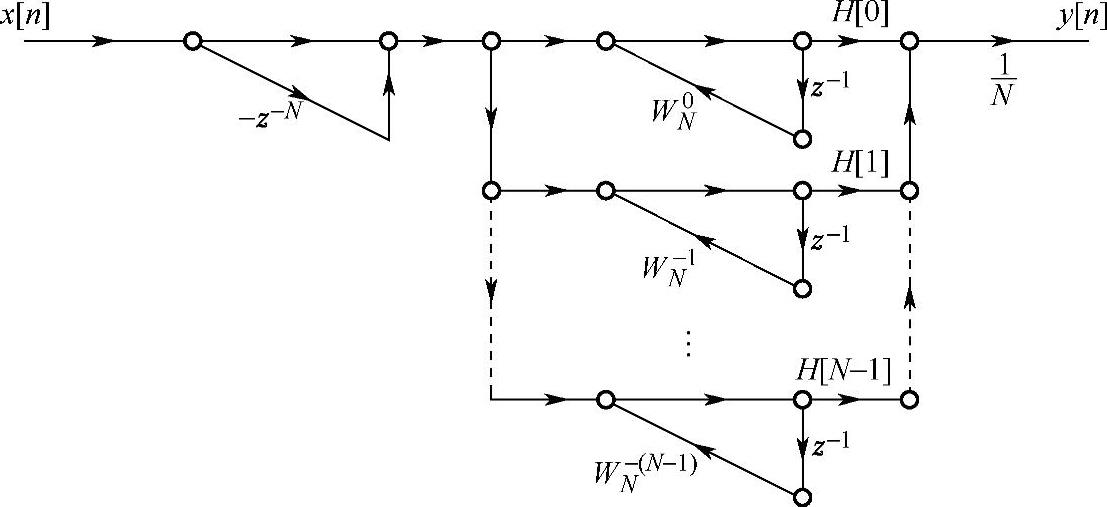
图4.5.3 FIR滤波器的频率抽样结构

频率抽样结构的特点是它的系数H[k]就是滤波器在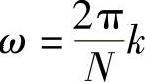处的响应，因此控制滤波器的频率响应很方便。但是结构中所乘的系数H[k]及W^-k_N都是复数，增加了乘法次数和存储量，而且所有极点都在单位圆上，由系数W^-k_N决定，这样，当系数量化时，这些极点会移动，有些极点就不能被梳状滤波器的零点所抵消（零点由延时单元决定，不受量化的影响）。系统就不稳定了。

频率抽样结构的主要优点如下：

1）在频率抽样点ω_k，有H（e^jωk）=H[k]，只要调整H[k]即一阶系统H′（z）中乘法器的系数，就可以有效地调整有限冲激响应滤波器的频响特性，使实际调整方便。

2）只要h[n]长度N相同，对于任何频响形状，其H_c（z）部分和任一H′（z）的结构完全相同，所不同的仅是各支路增益H[k]。因此相同部分便于标准化、模块化。

频率抽样结构的主要缺点如下：

1）系统稳定是靠位于单位圆上的N个零极点相互抵消保持的，实际上，寄存器都是有限长度的，这样有限字长效应加上子系统中各支路增益W^-k_N量化时产生的量化误差，可能使零极点不能完全抵消，从而影响系统的稳定性。

2）结构中H[k]和W^-k_N一般为复数，要求乘法器完成复数乘法运算，这对硬件实现是比较麻烦的。

针对上述缺点，可采取一定的措施对图4.5.3所示的结构予以修正，以减小这些不利因素。

首先，将单位圆上的零极点向单位圆内收缩一点，收缩至半径为r的圆上，取r＜1且r≈1，此时H（z）为

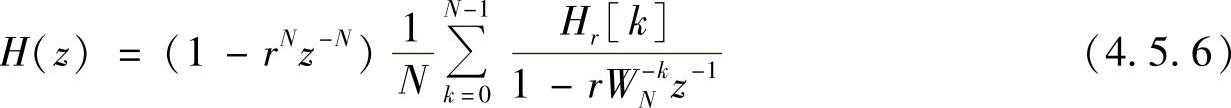
式中，H_r[k]表示在r圆上对H（z）的N等分等间隔抽样。由于r≈1，所以有H_r[k]≈H[k]，此时得到的H（z）与单位圆抽样得到的H（z）大致相等。此时零极点均为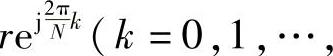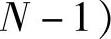。若由于某些原因，零、极点不能很好抵消时，极点位置仍在单位圆内，系统仍保持稳定。

其次，由离散傅里叶变换的共轭对称性可知，若h[n]为实数序列，则其离散傅里叶变换H[k]关于N/2点共轭对称。即H[k]=H^∗[N-k]，而且（W^-k_N）^∗=W_N^-（N-k），各并联支路的极点为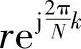（k=0，1，…，N-1）。为使系数为实数，可将共轭根合并，在z平面上这些共轭根在半径为r的圆周上以实轴为轴成对称分布，即z_N-k=z^∗_k，也就是

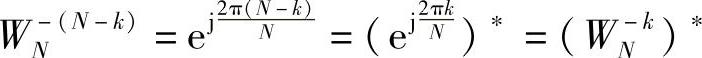
故可将结构中第k条支路和第N-k条支路合并为一个二阶网络，并记为H_k（z），则

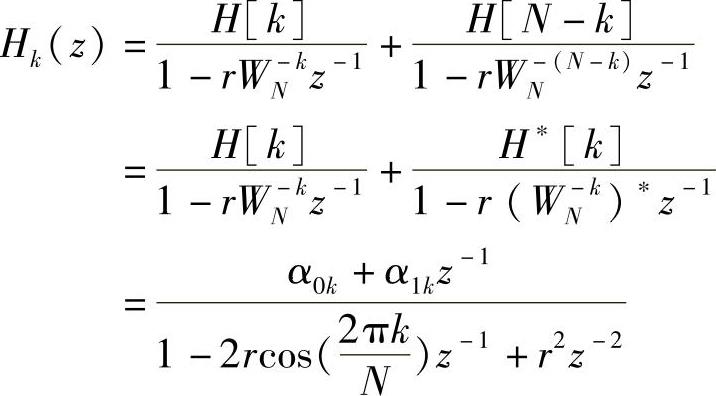
式中

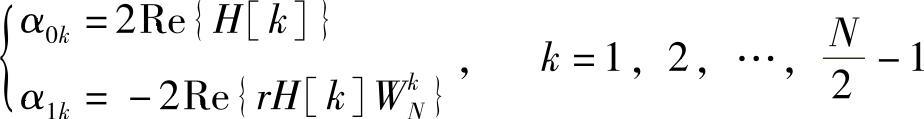
显然二阶系统H_k（z）的系数都是实数，其结构如图4.5.4a所示。

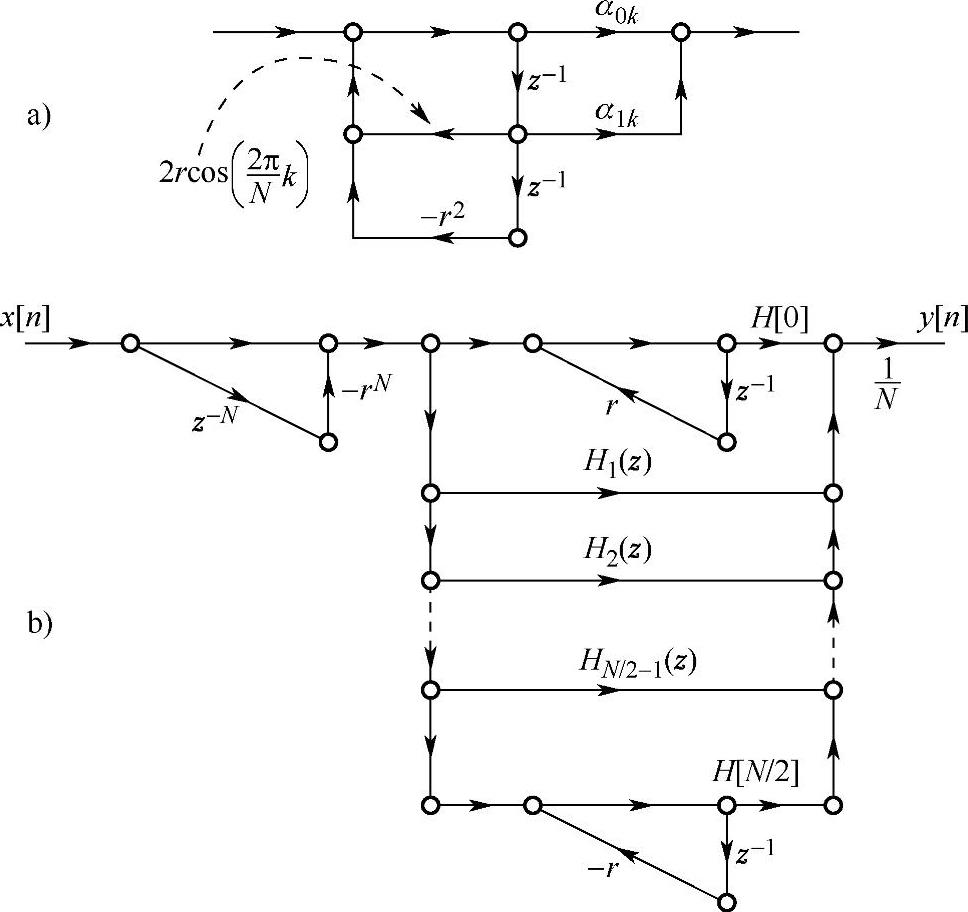
图4.5.4 频率抽样修正结构

当N为偶数时，H（z）可表示为

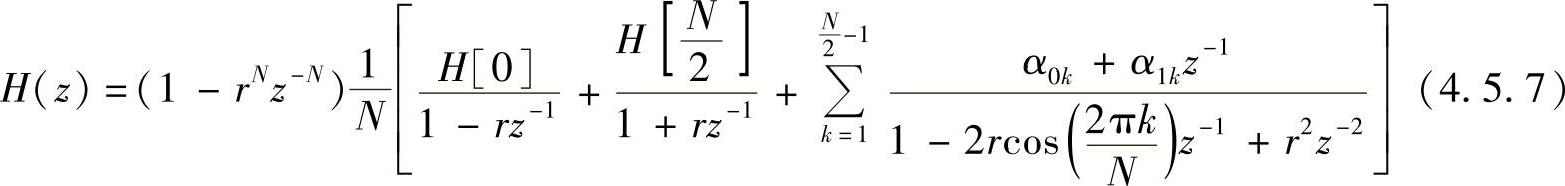
式中，H[0]和H[N/2]为实数，有两个实根，无需合并。式（4.5.7）对应的改进的频率抽样结构如图4.5.4b所示。

当N为奇数时，H（z）可表示为

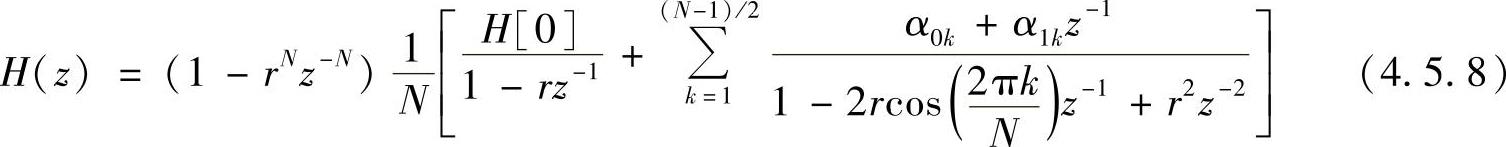
式中，H[0]为实数，只有一个实根。其对应的结构与图4.5.4b相似，请读者自己画出。

图4.5.4b中的任一H_i（z）的结构均为图4.5.4a的结构，这种改进的频率抽样结构克服了一般频率抽样结构的缺点。由图4.5.4可以看出，当抽样点数N很大时，其结构显得很复杂，需要的乘法器和延时单元很多，但对于窄带滤波器，大部分抽样值H[k]均为0，从而使二阶系统个数大大减少，所以频率抽样结构适用于窄带滤波器。