在许多实际应用，如图像处理中，要求数字滤波器具有线性相位。具有线性相频特性的滤波器系统函数H（ejω）为
式中，θ（ω）=-τω为滤波器的相位响应函数，是ω的线性函数（即线性相频特性）；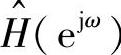
是滤波器的幅度响应函数，是ω的实函数。
如果有限冲激响应滤波器的单位抽样响应h[n]为实数（0≤n≤N-1），且满足
h[n]=±h[N-1-n] （0≤n≤N-1） （4.4.2）
式中，“+”号代表偶对称，“-”号代表奇对称，则此时的有限冲激响应滤波器是线性相位的。式（4.4.2）说明h[n]对（N-1）/2是偶对称或奇对称的。下面从式（4.4.2）出发推导线性相位有限冲激响应滤波器结构。
设h[n]=h[N-1-n]，N为偶数时，其频率特性为
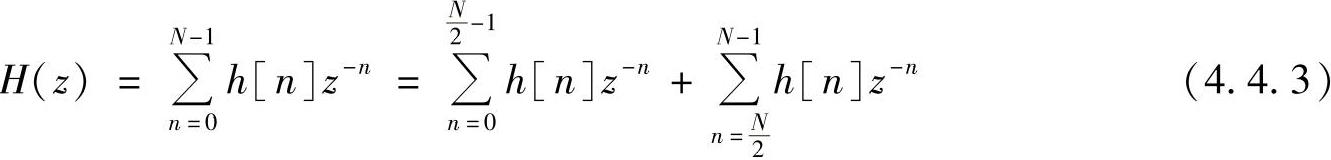
对式（4.4.3）中第二个求和项令m=N-1-n，则得
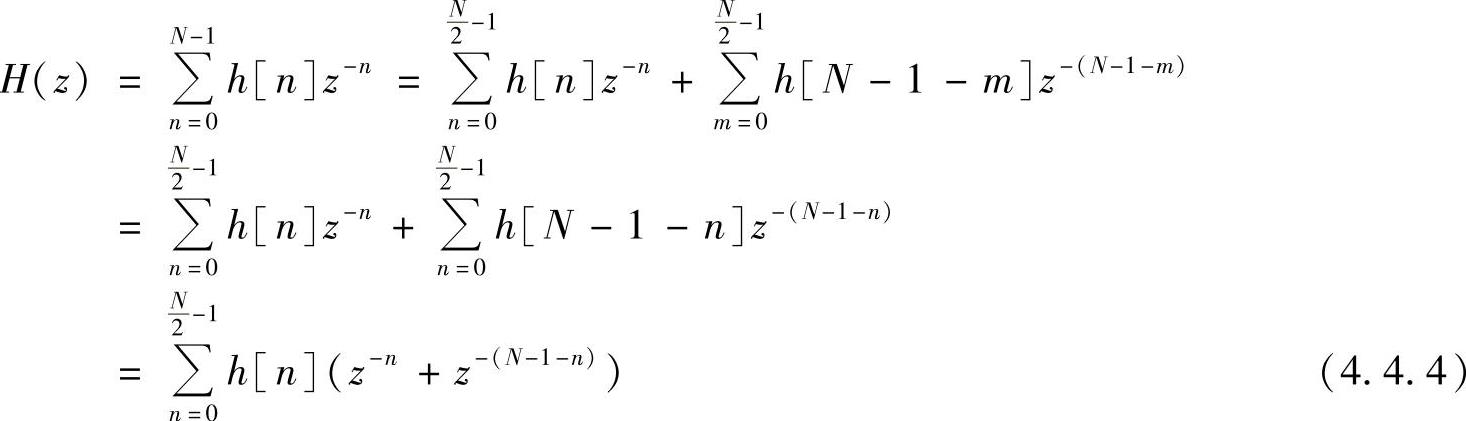
将z=ejω代入式（4.4.4），得
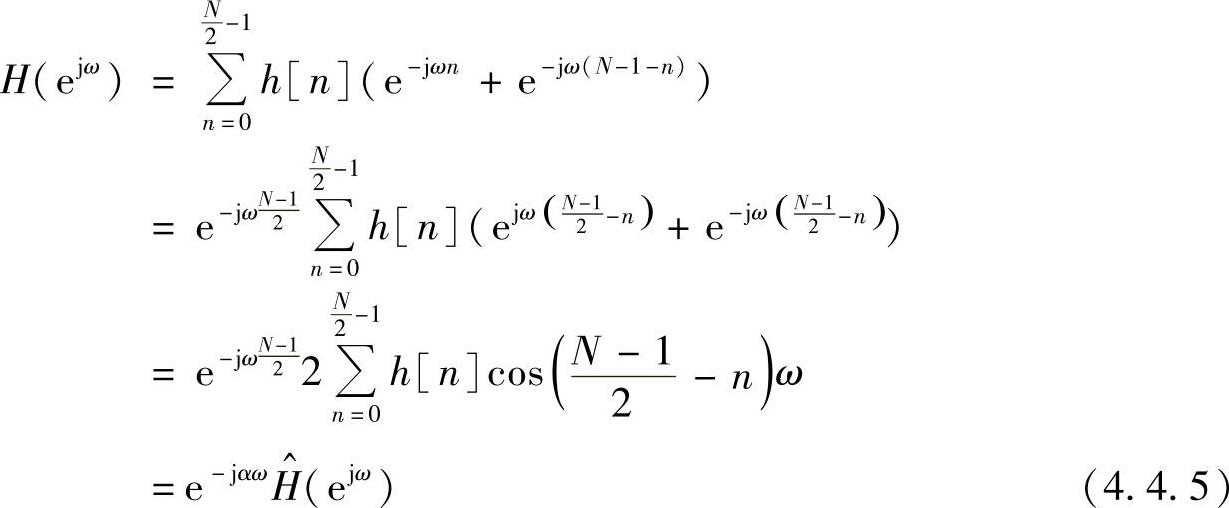
式中
由式（4.4.5）可以得出其中相移常数α=（N-1）/2，在给定序列长度N时，α是一常数，因而系统的群延时
τ为常数，说明该系统不存在线性失真，也就是说信号的不同频率分量通过系统时其延时相等。
从式（4.4.4）可知h[n]偶对称，且N为偶数时的网络结构形式，如图4.4.1所示。从图可以看出所需的乘法次数是N/2（注意：图4.3.1的结构需要N次乘法）。
设h[n]=h[N-1-n]，N取奇数，其频率特性为
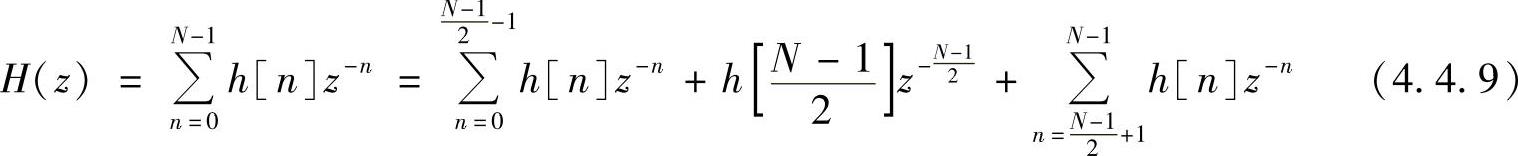
对式（4.4.9）中最后一个求和项令m=N-1-n，则得
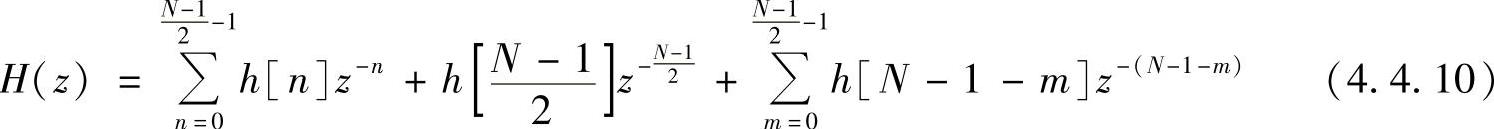
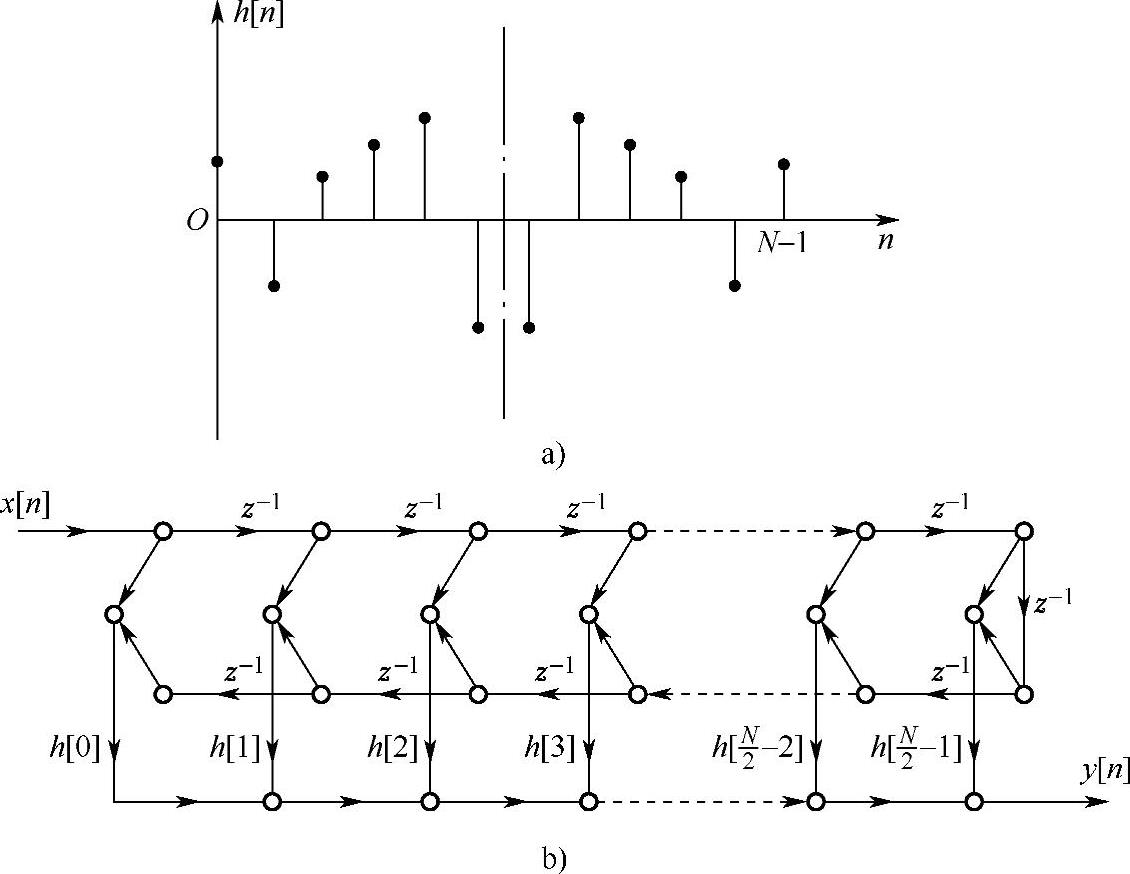
图4.4.1 偶对称h[n]（N=偶数）及其结构流图
将式（4.4.2）代入式（4.4.10），并化简得
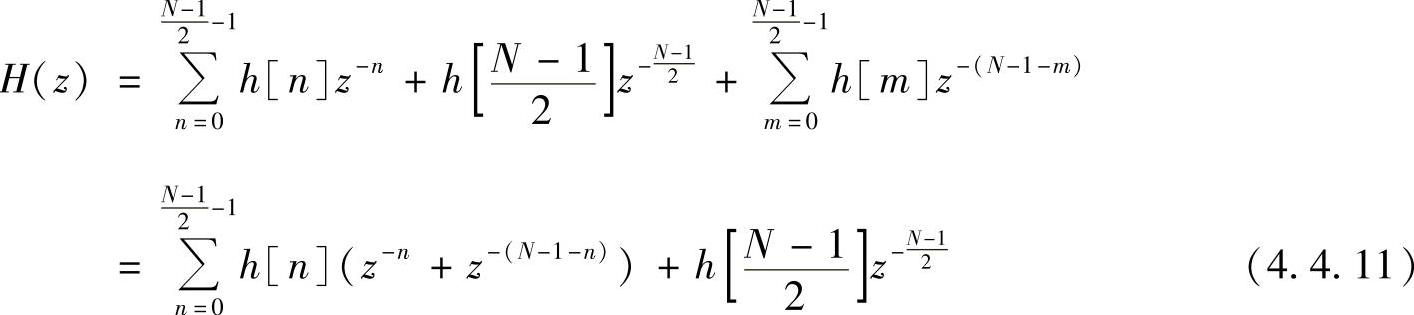
根据式（4.4.11）画出的直接结构形式如图4.4.2所示。由图可以看出所需的乘法次数为（N+1）/2，而不像图4.3.1所示的结构那样需要N次乘法。
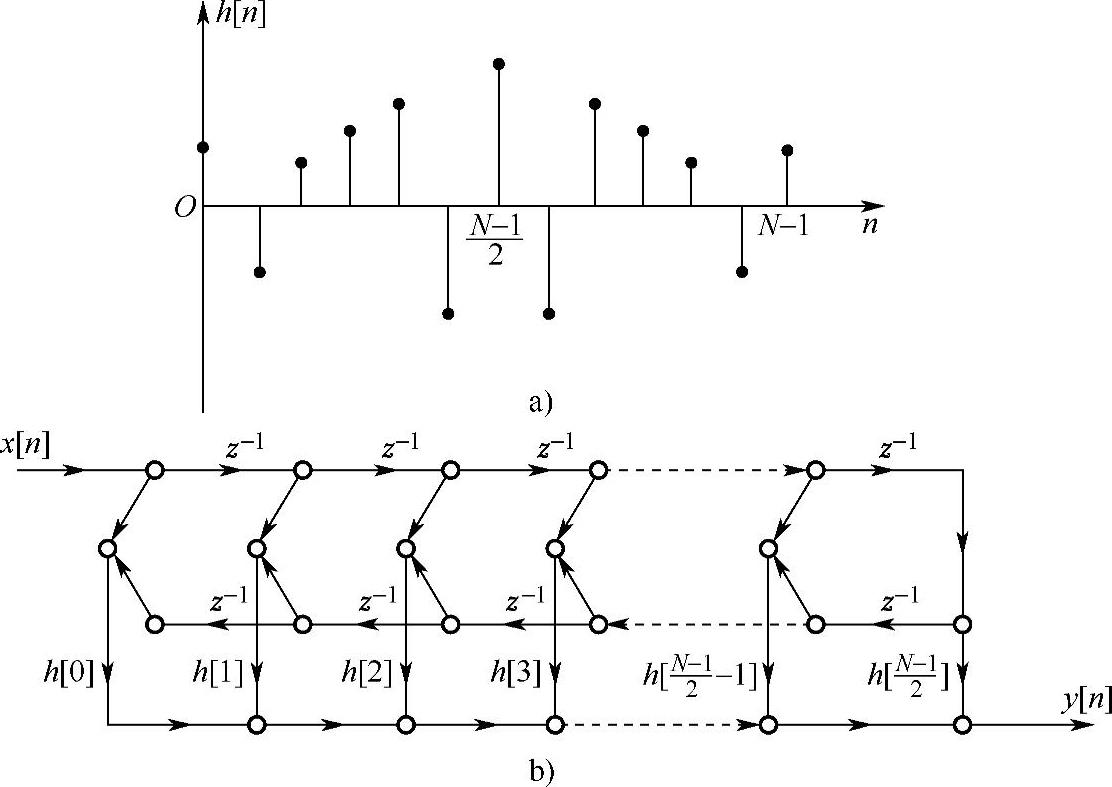
图4.4.2 偶对称h[n]（N=奇数）及其结构流图
同理可以证明，h[n]满足奇对称h[n]=-h[N-1-n]条件时，对应的频率特性为
式中
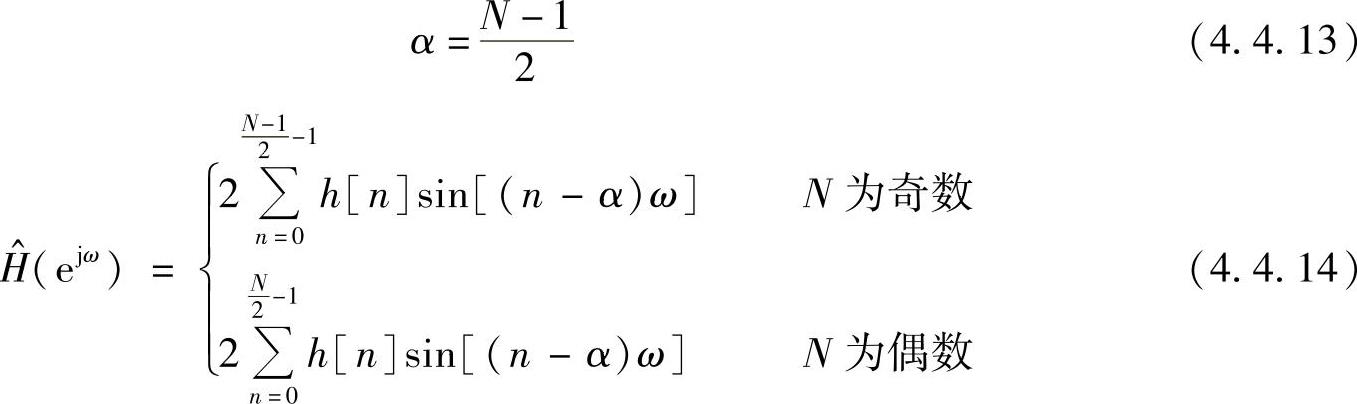
式（4.4.12）与式（4.4.5）相比，相移常数中增加了常数相移π/2，但它的群延时仍等于α，因而还是属于线性相位系统。
满足式（4.4.1）所示的奇对称条件的h[n]如图4.4.3a和图4.4.4a所示，其中图4.4.3a是N=偶数的情况，图4.4.4a是N=奇数的情况。它的直接形式结构图与具有偶对称条件的h[n]的结构相似，只是将后者的延时相加改换成了延时相减。另外，在N为奇数时，满足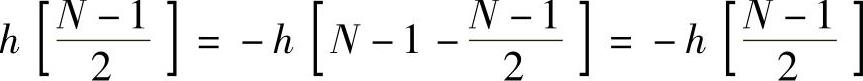
，因而
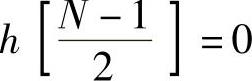，即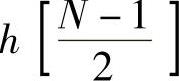
项不存在。具体流图结构如图4.4.3b和图4.4.4b所示。
利用线性相位系统的对称条件，在实现上可以减少乘法次数，从而简化了结构。线性相位有限冲激响应系统除去直接形式外，同样存在级联形式的结构，和一般的有限冲激响应系统相似，对多项式H（z）进行因式分解就可以得到相应的级联形式，但考虑到线性相位h[n]的对称性，H（z）的零点分布还必须满足一定的条件。
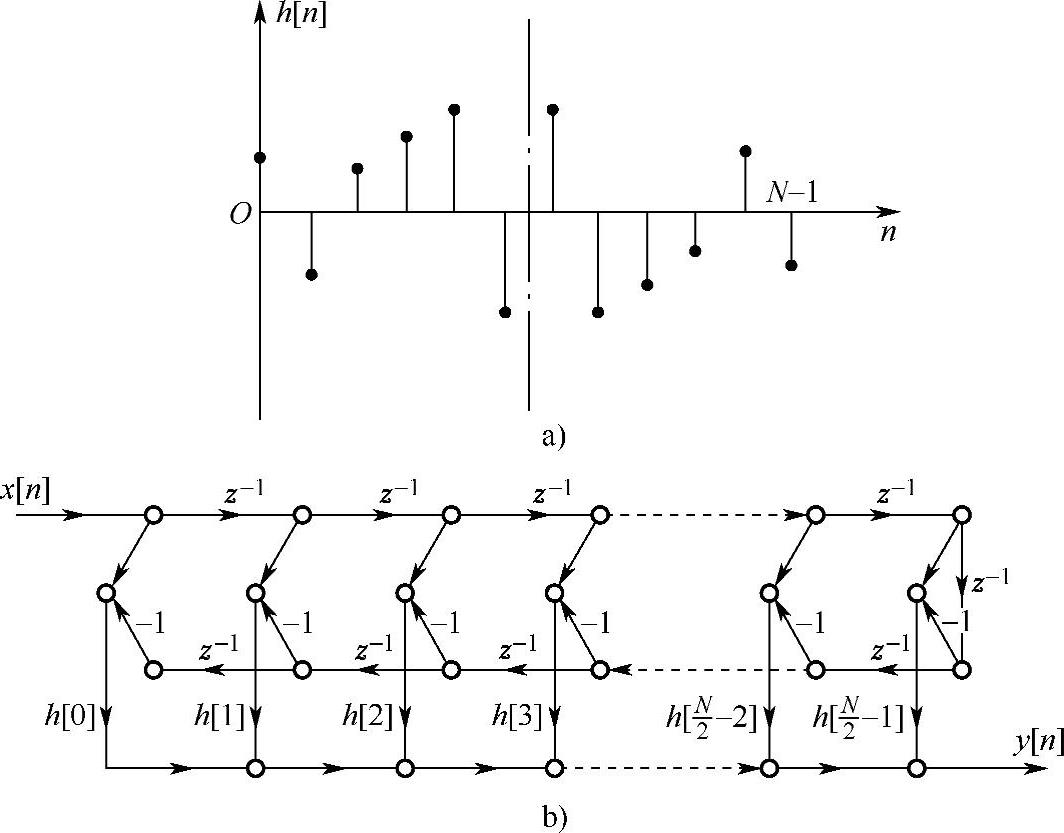
图4.4.3 奇对称h[n]（N=偶数）及其结构流图
线性相位有限冲激响应滤波器的零点分布特点如下：
当h[n]=h[N-1-n]时
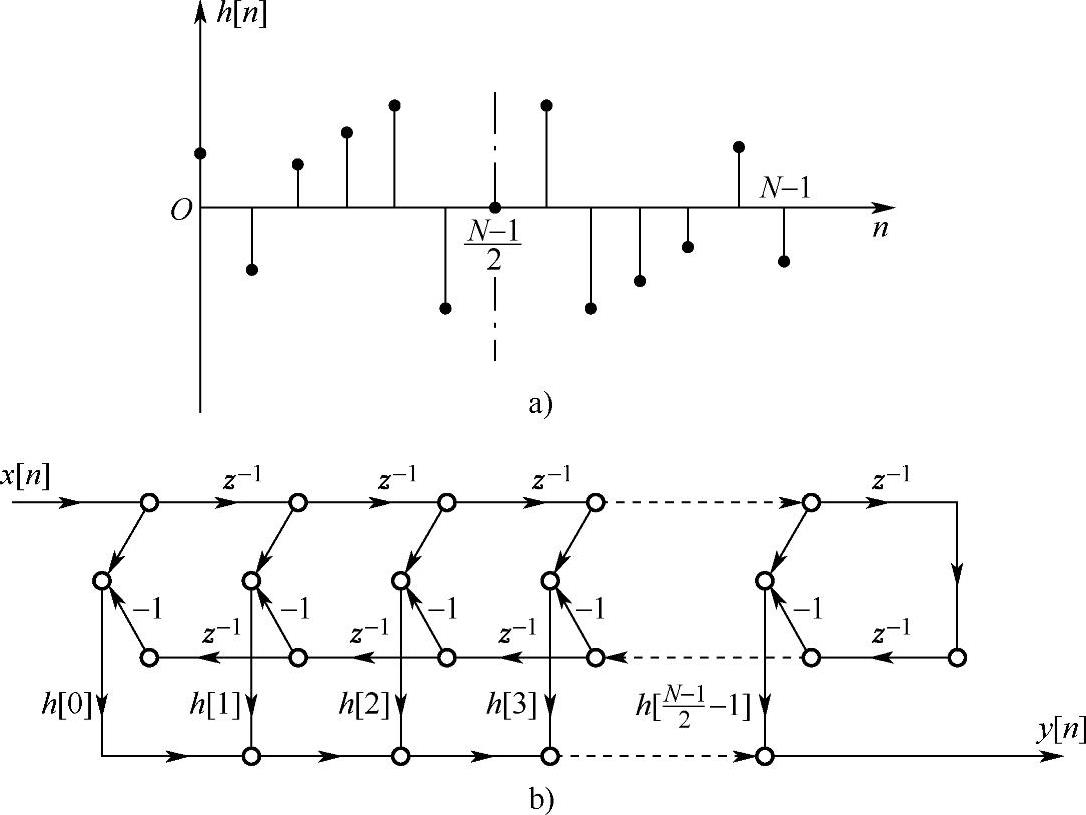
图4.4.4 奇对称h[n]（N=奇数）及其结构流图
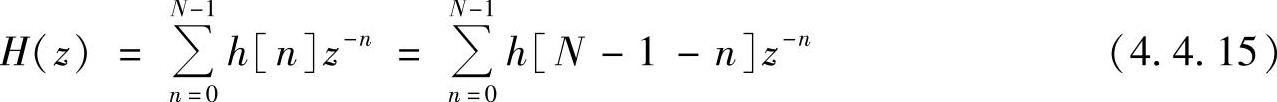
令m=N-1-n，则
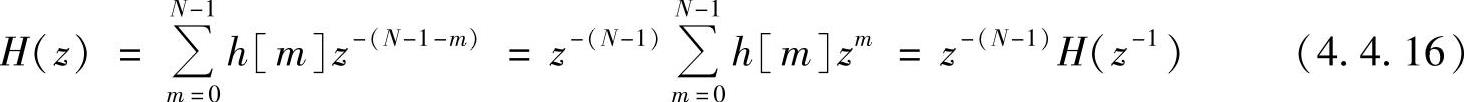
当h[n]=-h[N-1-n]时，同理可得
H（z）=-z-（N-1）H（z-1） （4.4.17）
由式（4.4.16）、式（4.4.17）可知，线性相位有限冲激响应滤波器的系统函数具有如下的零点分布特点。
1）若z=zi是零点，H（zi）=0，则它的倒数z=zi-1也必定是零点。这是因为
H（zi-1）=±z（N-1）iH（zi）=0
2）由于h[n]是实数，故H（z）的零点必须以共轭对出现，所以z=z∗i和z=（z∗i）-1也一定是零点。
这种互为倒数的共轭对有以下几种可能的情况（见图4.4.5）：
1）zi既不在实轴上又不在单位圆上，此时必然是四个互为倒数的两组共轭对，四个零点z1，
，z∗1，
同时出现。(www.xing528.com)
2）zi是实数又不在单位圆上，其共轭也就是zi本身，则两个零点z2，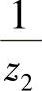
同时出现。
3）zi是单位圆上的复零点，其共轭倒数就是其本身，则两个零点z3，z∗3同时出现。
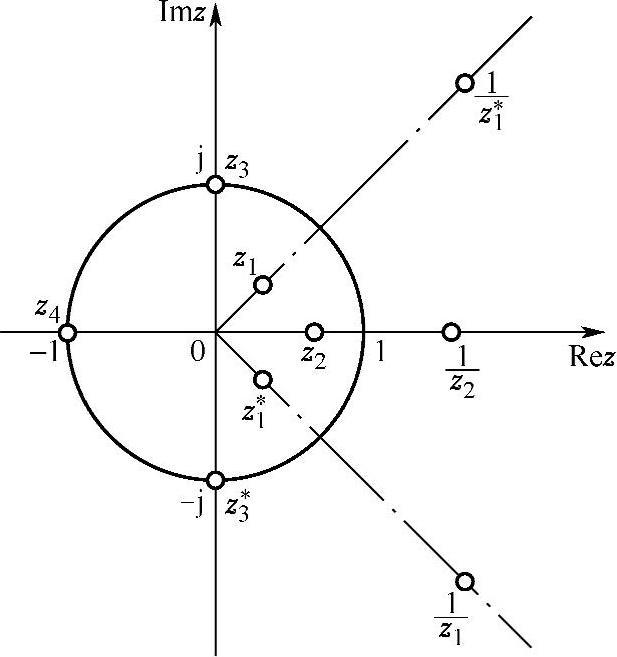
图4.4.5 线性相位FIR系统的零点分布
4）zi是实数又在单位圆上，则四点合一，即z4点。
按照这四种零点分布情况就可以知道，线性相位级联形式的结构分别由四阶、二阶和一阶子系统串联而成。位于单位圆内的复零点z1及其共轭、镜像反演对称的零点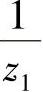
，z∗1，
可以构成一个四阶实系数的子系统，即有
H1（z）=（1-z1z-1）（1-z1∗z-1）（1-z-1/z1）（1-z-1/z∗1）
令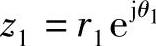
，则
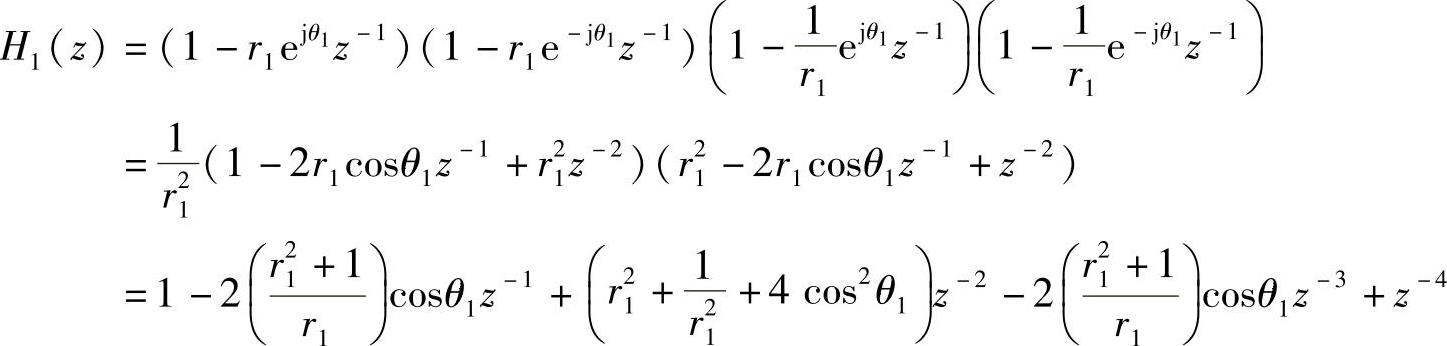
令
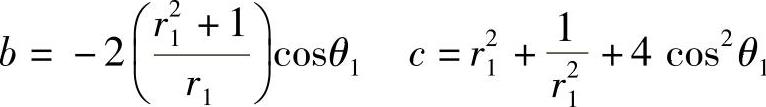
则得
H1（z）=1+bz-1+cz-2+bz-3+z-4 （4.4.18）
从式（4.4.18）可以看出，H1（z）本身也是线性相位的，图4.4.6画出了H1（z）的线性相位直接形式结构流图。对式（4.4.18）所示的四阶子系统也可以用二阶子系统级联来实现，如图4.4.7所示。
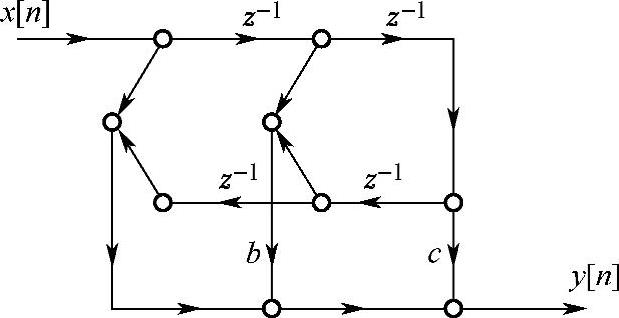
图4.4.6 四阶线性相位子系统
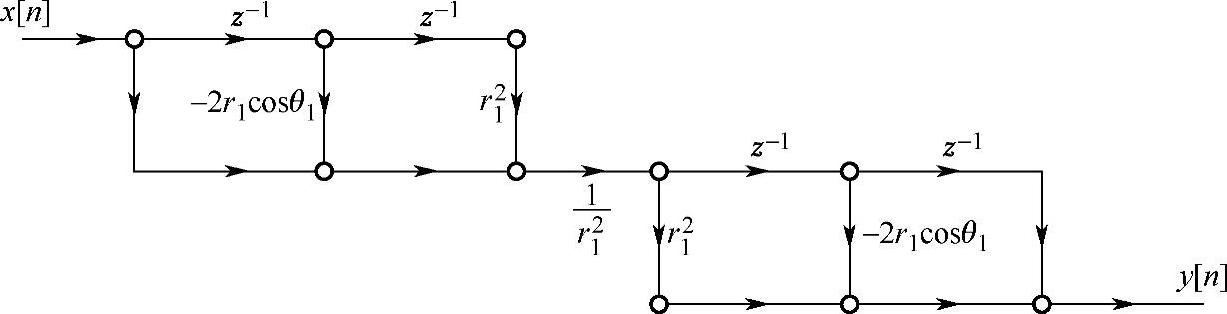
图4.4.7 二阶子系统的级联
对于位于实轴上而又不在单位圆上的实零点z2=r2，构成的子系统是二阶的，即
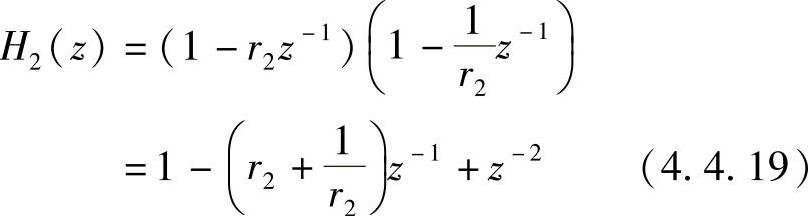
式（4.4.19）所描述的子系统显然是线性相位的，其网络结构如图4.4.8所示。
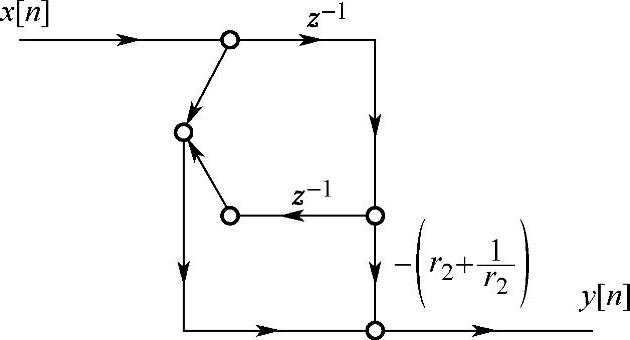
图4.4.8 位于实轴上而又不在单位圆上的实零点组成的子系统流图
位于单位圆上而又不在实轴上的复零点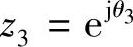
、
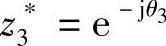所构成的子系统为
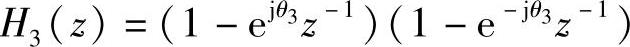
其网络结构与图4.4.8相同，只是把系数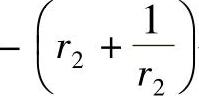
换成-2cosθ3即可。
位于单位圆上又在实轴上的实零点z4=±1，则构成的一阶子系统可表示为
H4（z）=1∓z-1 （4.4.21）由此可见，当N为偶数时，H（z）有奇数个零点，其中含z=±1的零点必为奇数个；当N为奇数时H（z）有偶数个零点，如果含有z=±1的零点，则必是偶数，否则就没有z=±1的零点。
由上面分析可知，线性相位有限冲激响应系统的系统函数H（z），用级联形式结构实现时，可以分别由一阶、二阶、四阶子系统级联而成，并且每一子系统都是线性相位的，由此级联而成的整个系统也必保持线性相位的特性。
【例4.4.1】 已知一有限冲激响应系统的系统函数为
H（z）=1-2.05z-1+3.2025z-2-1.05z-3-1.05z-4+3.2025z-5-2.05z-6+z-7
求用级联形式实现的结构流图及零点分布。
解 由于H（z）中的N=8，因而必定有一个零点在z=±1处，由于最高阶z-7的系数为正，因而在z=-1点处有一个零点，由此可得H4（z）=1+z-1。H（z）除以H4（z）后余下的多项式为
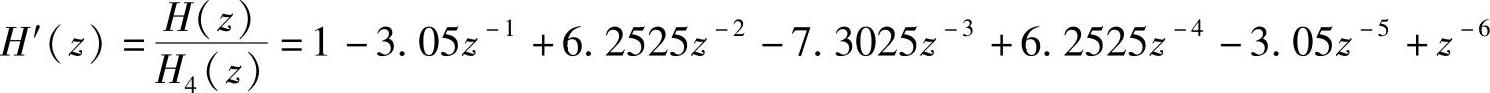
H′（z）的最高阶次N-1=6，因而有两个零点落在单位圆上，即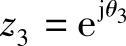
和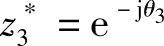
，故对应的二阶子系统的系统函数为
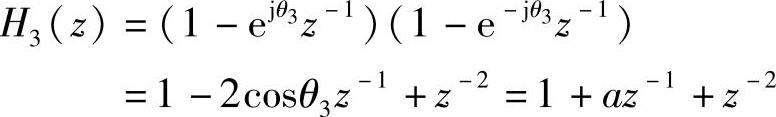
又设余下的四阶子系统为
H1（z）=1+bz-1+cz-2+bz-3+z-4
因为H′（z）=H1（z）H3（z）和H1（z）、H3（z）展开式比较系数间的关系，可得
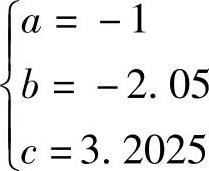
所以有-2cosθ3=-1，解得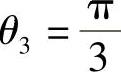
。再利用
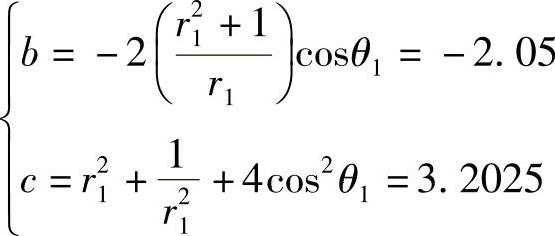
解上述联立方程，得
所以七个零点分别为
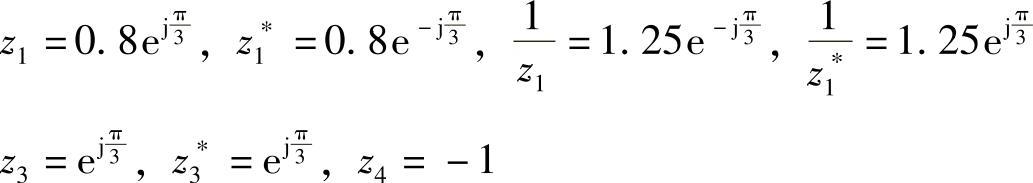
这样，H（z）的零点分布如图4.4.9所示，级联形式的结构流图如图4.4.10所示。
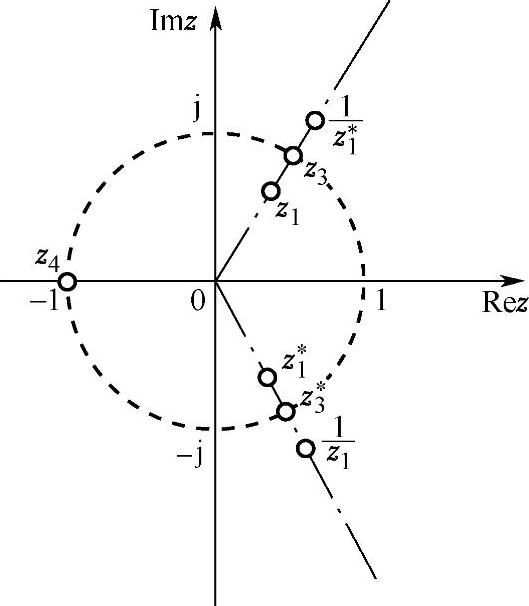
4.4.9 例4.4.1的零点分布图
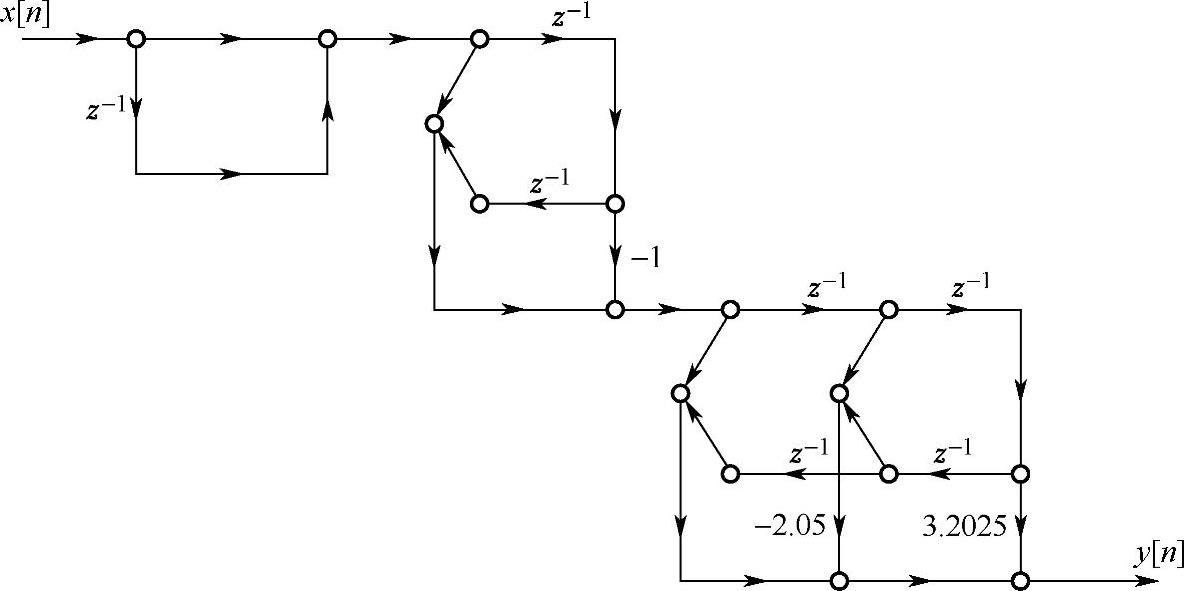
图4.4.10 例4.4.1的级联形式结构流图
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
