级联形式的实现方法及影响因素

将系统函数按零、极点进行因式分解，得

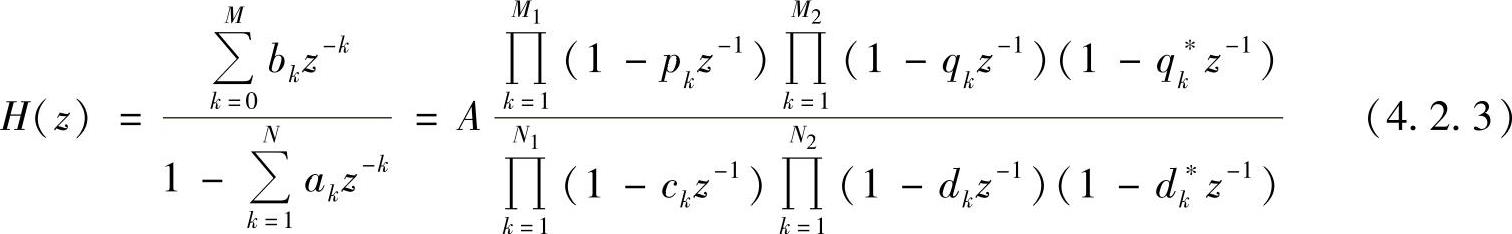
式中，M=M₁+2M₂，N=N₁+2N₂；p_k、c_k表示一阶因子中的实零点和实极点；q_k，q_k^∗和d_k，d_k^∗分别表示因式中的共轭零点和共轭极点。如果把具有共轭复根的两个一阶因式合并，则各子系统可以表示为具有实系数的二阶系统的形式，即有

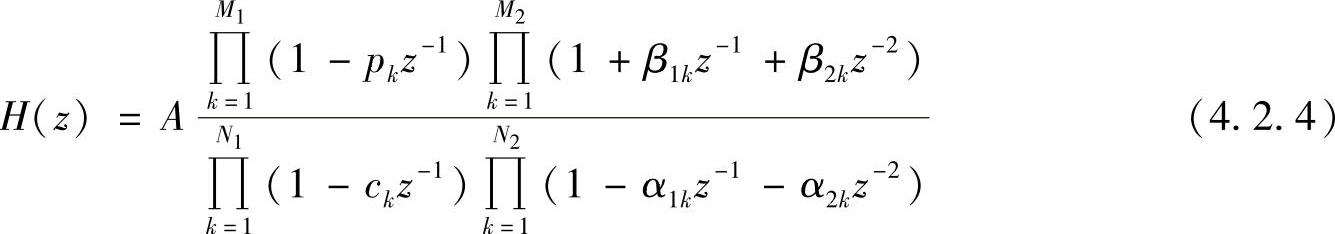
为了方便，分子取正号，分母取负号，这样流图上的系数均为正。为统一起见，把分子分母中的一阶子系统看作α₂和β₂为零的二阶子系统特例，于是可写出把H（z）分解为实系数的二阶子系统的级联形式，即

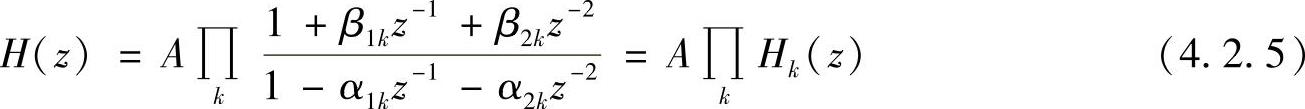
式（4.2.5）表示H（z）的级联分解形式，其每一子系统为二阶基本节，如果用如图4.2.3的直接Ⅱ型实现二阶子系统，则整个系统就具有最少存储单元的级联结构形式。

【例4.2.1】 给定

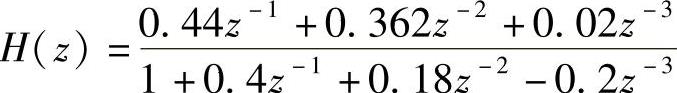
求其级联实现的结构图。(www.xing528.com)

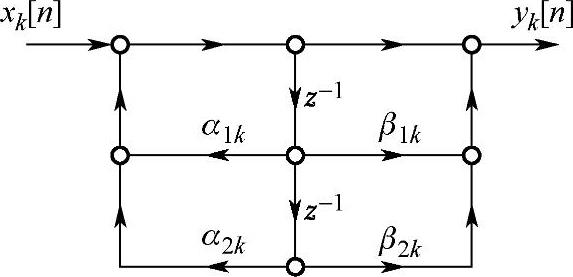
图4.2.3 二阶子系统的直接Ⅱ型实现

解 为了用级联形式实现，必须将H（z）分解成二阶实系数的子系统，对分子、分母多项式进行分解得

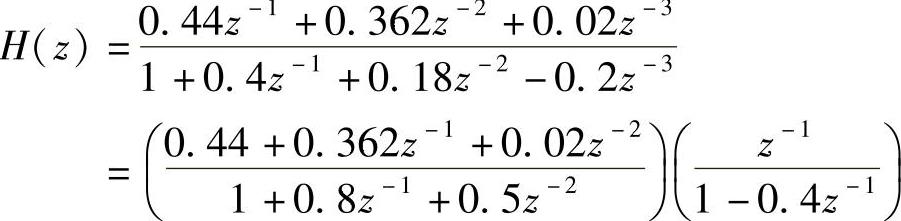
由此得到其级联形式如图4.2.4所示。

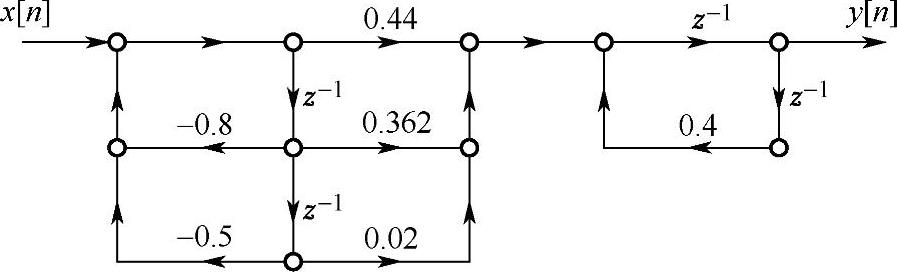
图4.2.4 例4.2.1级联流图

级联形式结构的主要优点是存储单元少，当用硬件实现时，一个二阶节可以分时使用，这种时分复用使硬件结构简化。另一个重要优点是每一个二阶节是相互独立的，而且各自代表一对零点和极点，这样调整系数α_1k，α_2k和β_1k，β_2k也就是单独调整第k对极点和零点，不影响其他零、极点的分布，因而滤波器的性能可通过分别调整单独的零、极点分布而得到控制。

级联形式中另一个需要考虑的问题是有限字长的影响。理论上各子系统的前后次序排列可以任意组合，但对有限精度运算来说不同组合有不同的量化效应，其运算误差差别甚大；其次，各级之间电平大小的搭配会影响输出信号的精度，太大的电平会产生溢出，太小的电平会影响输出的信噪比，因而在具体考虑时需要分情况不同对待。