【摘要】：无限冲激响应系统的转移函数为其对应的差分方程为式结构流图如图4.2.1所示。可以看出，这个流图是直接根据式差分方程得出的，它是两个子系统的级联：第一级实现了系统对应的零点部分，第二级实现了系统对应的极点部分。图4.2.1 IIR滤波器直接Ⅰ型图4.2.2 IIR滤波器直接Ⅱ型从直接Ⅰ型结构流图可以看出延时单元是比较多的。
无限冲激响应系统的转移函数为
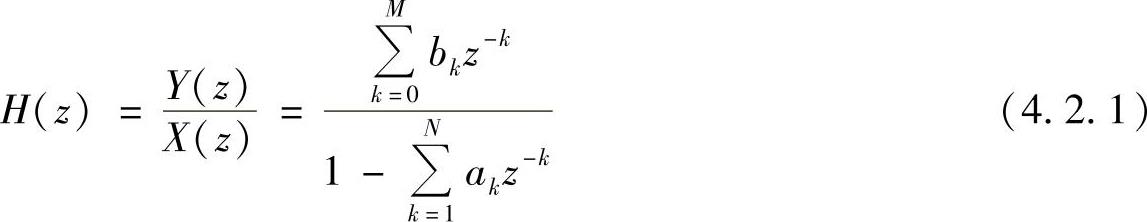
其对应的差分方程为
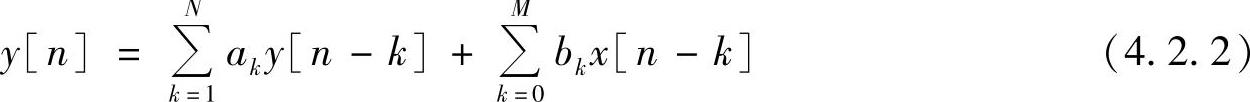
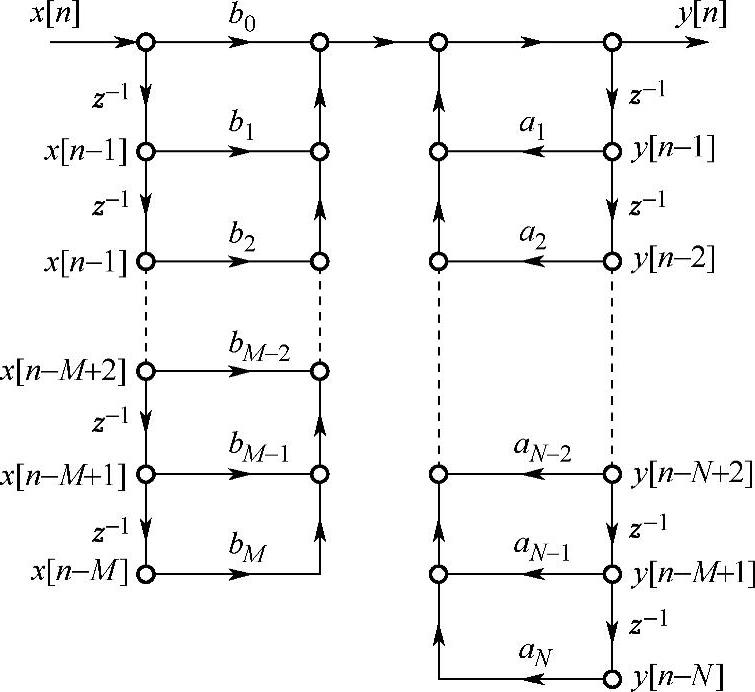
式（4.2.2）结构流图如图4.2.1所示。可以看出，这个流图是直接根据式（4.2.2）差分方程得出的，它是两个子系统的级联：第一级实现了系统对应的零点部分，第二级实现了系统对应的极点部分。用这样结构实现的称为直接Ⅰ型。
(www.xing528.com)
图4.2.1 IIR滤波器直接Ⅰ型
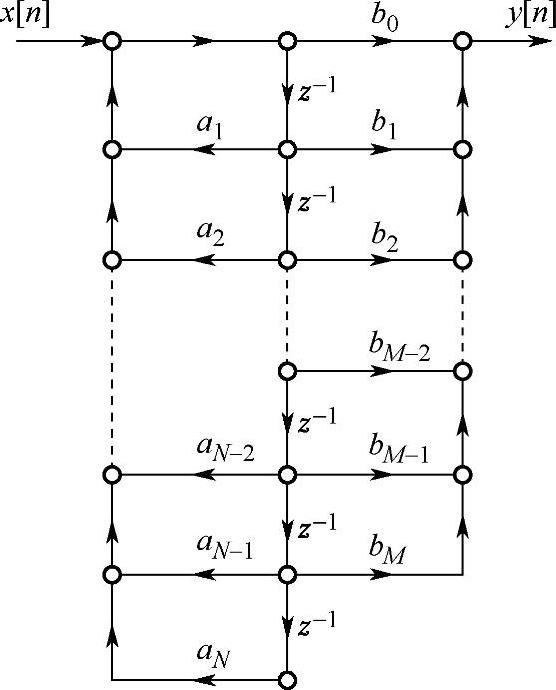
图4.2.2 IIR滤波器直接Ⅱ型
从直接Ⅰ型结构流图可以看出延时单元是比较多的。如果把零极点实现次序对换一下，即先实现极点再实现零点，且把延时单元合并成一个公用的，则构成了图4.2.2所示的结构形式，称之为直接Ⅱ型。这个结构形式与直接I型比较，延时单元减少了一半。用直接Ⅱ型实现式（4.2.1）的H（z），所需的延时单元数为max（N，M）。由于这种实现所需延时单元数目最少，因而也被称为典范形式网络（Canonic Form Networks）结构。
直接形式网络结构的主要特点是简单直观，根据差分方程或转移函数用梅逊公式可以直接画出它所对应的流图，而且延时单元最少；缺点是系数ak及bk对滤波器性能的控制不直接，每一系数的变化都将影响零点或极点分布，使滤波器调整不方便，而且对有限字长的影响较大，或者说量化的灵敏度较高。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
