【摘要】：如果线性调频z变换用基2快速傅里叶变换实现，那么按图3.8.4所示的实现框图可以统计出所需的运算量。图3.8.4 用FFT实现CZT框图1）计算f[n]需N次乘法。3）一般H[k]=DFT{h[n]}无需现场计算，因为h[n]是已知的，可以事先计算H[k]。因而总共需要的乘法次数mc为可见其运算量比直接计算所需的NM次乘法明显减少了。总之，与离散傅里叶变换相比，线性调频z变换算法有以下特点：1）输入序列长度与输出序列长度不必相等。
如果线性调频z变换用基2快速傅里叶变换实现，那么按图3.8.4所示的实现框图可以统计出所需的运算量。
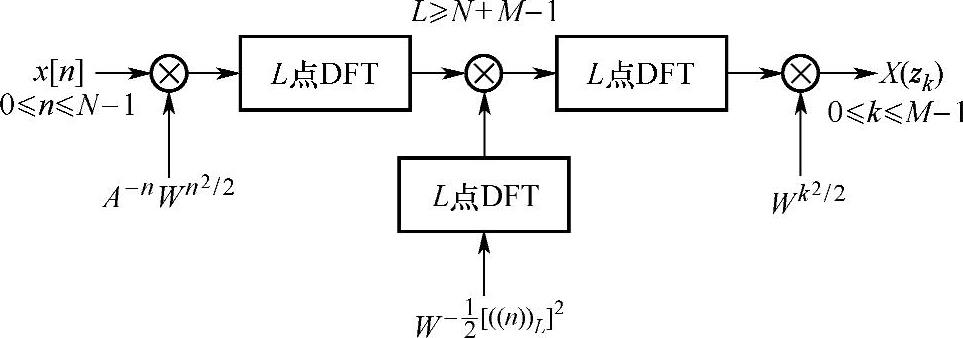
图3.8.4 用FFT实现CZT框图
1）计算f[n]需N次乘法。
2）计算Y[k]=DFT{y[n]}需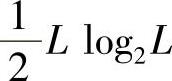
乘法，为简单计，设L=N+M-1，则计算Y[k]需
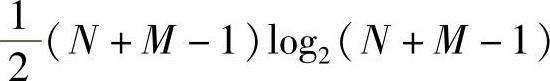次乘法。
3）一般H[k]=DFT{h[n]}无需现场计算，因为h[n]是已知的，可以事先计算H[k]。
4）计算V[k]=Y[k]·H[k]需L=N+M-1次乘法。
5）计算v[n]=IDFT{V[k]}需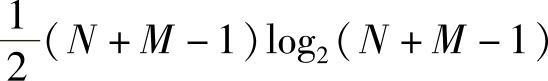
次乘法。
6）计算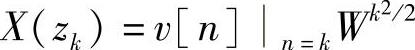
需M次乘法。
因而总共需要的乘法次数mc为(www.xing528.com)
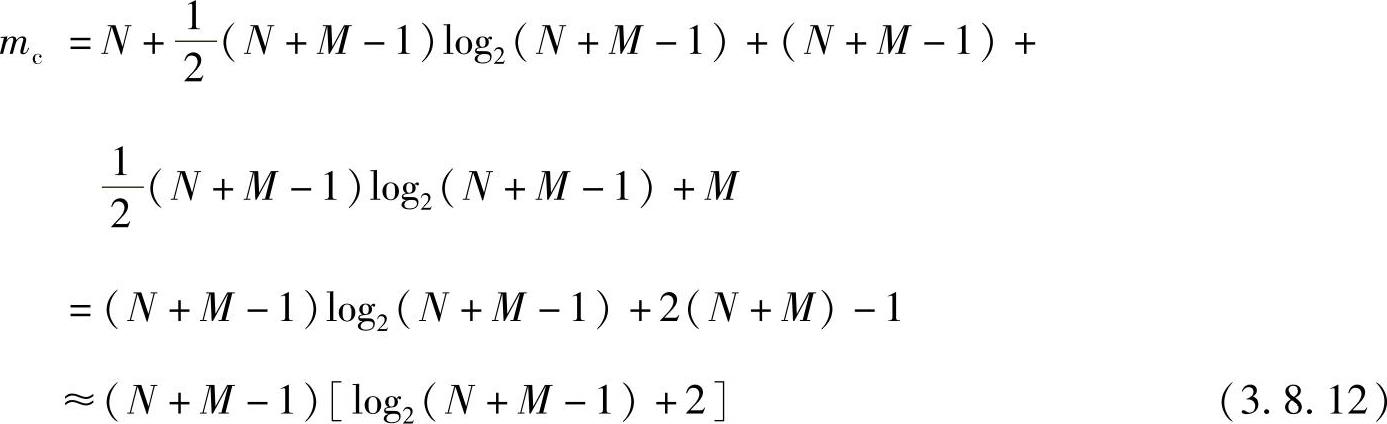
可见其运算量比直接计算所需的NM次乘法明显减少了。
总之，与离散傅里叶变换相比，线性调频z变换算法有以下特点：
1）输入序列长度与输出序列长度不必相等。
2）M和N可以不是组合数，甚至可以为素数。
3）zk点的间隔φ0是任意的，因此频率分辨力也是任意的。
4）周线不必是圆，这对分析在单位圆内的极点很有好处。
5）起始点z0不必在z=1处，可以在任意频率开始计算，因而适用于窄带高分辨力的计算；
6）若A=1，M=N，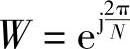
，则线性调频z变换即为离散傅里叶变换，因此离散傅里叶变换可以用线性调频z变换算法计算，即使N为素数也可以。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
